ekspertyza: Intermediate
Co to jest funkcja splajnu?
zanim zastanowimy się, jak skonstruować dla nich system bazowy, musimy wiedzieć, jakie są podstawowe cechy splotów.
funkcje splajnu powstają poprzez łączenie wielomianów ze sobą w ustalonych punktach. Oznacza to, że przedział rozciągający się od dolnej granicy TL granicy tu, przez którą chcemy przybliżyć krzywą do L+1 sub-interwałów oddzielonych przez L wewnętrzne granice ξl zwane węzłami, lub czasami punktami przerwania.)Istnieje rozróżnienie między tymi dwoma pojęciami, ale do tego dojdziemy później.
rozważmy najprostszy przypadek, w którym pojedynczy punkt przerwania dzieli interwał na dwie podinterwale. Splinefunkcja jest, w każdym przedziale, wielomianem o określonym stopniu (najwyższa moc definiująca wielomian) lub porządku (liczba współczynników definiujących wielomian, która jest o jeden więcej niż jego stopień). Użyjmy m do wyznaczenia kolejności wielomianu, tak aby stopień był m-1:
przy wewnętrznym punkcie przerwania ξ1 oba wielomiany muszą płynnie się łączyć. W najczęstszym przypadku oznacza to, że pochodne dopasowują się do rzędu o jeden mniej niż stopień. W rzeczywistości, gdyby pasowały do pochodnej, której kolejność równa się stopniowi, byłyby tym samym wielomianem. Tak więc zdefiniowana w niej funkcja splajnu ma jeden dodatkowy stopień swobody niż wielomian rozciągający się na cały przedział.
na przykład niech każdy wielomian będzie odcinkiem prostej, a więc stopnia pierwszego. W tym, łączą się w punkcie przerwania z dopasowanymi pochodnymi do stopnia 0; w skrócie, po prostu łączą się i mają identyczne wartości w punkcie przerwania. Ponieważ pierwszy wielomian ma dwa stopnie swobody (nachylenie i punkt przecięcia), a drugi, mający swoją wartość już określoną w punkcie przecięcia,pozostaje tylko jeden stopień swobody (nachylenie), całkowita linia wielokąta ma trzy stopnie swobody.
odpowiednio, jeśli oba wielomiany są kwadratami, to dopasowanie zarówno pod względem wartości, jak i pod względem liczby pierwszej pochodnej ξ1. Pierwszy wielomian ma trzy stopnie swobody, ale drugi traci dwa, ponieważ jeśli jest ograniczony jego wartością i nachyleniem w ξi, a zatem zachowuje tylko jeden. Pozostawia to w sumie cztery stopnie swobody dla wielomianu kwadratowego w całym przedziale. Rysunek 1 przedstawia przypadki liniowe i kwadratowe z pojedynczym punktem przerwania.
Jakie są przykłady powszechnie używanych funkcji bazowych?
możemy teraz uogólnić sytuację na wewnętrzne punkty przerwania l, a funkcja splajnu jest rzędu m lub stopnia M – 1 nad każdym interwałem. Pierwszy segment wielomianu ma pełne dopełnienie m stopni swobody, ale każdy kolejny segment ma tylko jeden stopień swobody ze względu na ograniczenia m-1 dotyczące jego zachowania.Daje to w sumie L + M stopni swobody, czyli liczbę punktów przerwania plus kolejność odcinków wielomianu.
zatem funkcje splajnu są zasadniczo uogólnieniami pojęcia wielokątów. Swoją elastyczność uzyskują na dwa sposoby: Po Pierwsze, przez kolejność polynomiałów, z których są zbudowane, i po drugie, przez liczbę wykorzystywanych breakpointów. Zazwyczaj decydujemy się utrzymać porządek na stałym poziomie i dodawać punkty przerwania, aby uzyskać wymaganą elastyczność.
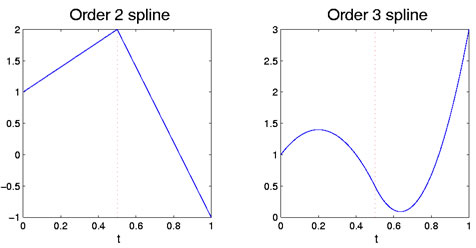
Rysunek 1: Lewy rysunek pokazuje funkcję splajnu o kolejności dwóch, która jest liniowa. Właściwa liczba to splajn rzędu 3, który jest fragmentarycznie kwadratowy. Punkt przerwania na 0,5 jest oznaczony czerwoną pionową przerywaną linią.