definicja
wielomian w zmiennej x jest funkcją, którą można zapisać w postaci,
gdzie an, an-1 , …, A2, a1, A0 są stałymi. Określeniem zawierającym największą potęgę x (tzn. anxn) nazywamy wyrażenie wiodące, a współczynnikiem wiodącym. Stopień wielomianu jest potęgą X w wyrazie wiodącym. Widzieliśmy już wielomiany stopnia 0, 1 i 2, które były odpowiednio funkcjami stałymi, liniowymi i kwadratowymi. Wielomiany stopnia 3, 4 i 5 mają również specjalne nazwy: funkcje sześcienne, kwartyczne i kwintyczne. Wielomiany o stopniu n > 5 nazywane są po prostu wielomianami n-tego stopnia. Nazwy różnych funkcji wielomianowych zestawiono w poniższej tabeli.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
ograniczające zachowanie wielomianów
ograniczające zachowanie funkcji opisuje, co dzieje się z funkcją jako x → ±∞. Stopień wielomianu i znak jego współczynnika wiodącego dyktują jego ograniczające zachowanie. W szczególności,
wyniki te są podsumowane w poniższej tabeli.
możesz użyć tej informacji, aby określić, czy wielomian ma nieparzysty lub parzysty stopień i czy współczynnik wiodący jest dodatni lub ujemny, po prostu sprawdzając jego Wykres.
poniższe wykresy wielomianów ilustrują każde z zachowań przedstawionych w powyższej tabeli.
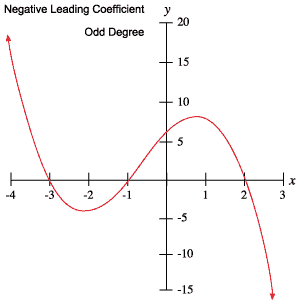
a punkty zwrotne
stopień wielomianu mówi o nim więcej niż zachowanie ograniczające. W szczególności wielomian n-tego stopnia może mieć co najwyżej n pierwiastków rzeczywistych (x-Przechwyty lub zera) liczących mnożenie. Na przykład, przypuśćmy, że patrzymy na wielomian 6 stopnia, który ma 4 różne pierwiastki. Jeśli dwa z czterech korzeni mają wielokrotność 2, a pozostałe 2 mają wielokrotność 1, wiemy, że nie ma innych korzeni, ponieważ uwzględniliśmy wszystkie 6 korzeni. Dzieje się tak, ponieważ korzenie o wielokrotności dwóch (znane również jako podwójne korzenie) są liczone jako dwa korzenie.
należy pamiętać, że wielomian n-tego stopnia nie musi mieć N rzeczywistych korzeni — może mieć mniej, ponieważ ma urojone korzenie. Zauważ, że wielomian stopnia nieparzystego musi mieć co najmniej jeden pierwiastek rzeczywisty, ponieważ funkcja dąży do – ∞ na jednym końcu i + ∞ na drugim; funkcja ciągła, która przełącza się z ujemnego na dodatni musi przecinać oś x gdzieś pomiędzy. Ponadto wielomian n-tego stopnia może mieć co najwyżej n-1 punkt zwrotny. Punkt zwrotny to punkt, w którym funkcja zmienia się ze rosnącego na malejący lub malejącego na rosnący, jak widać na poniższym rysunku. Ponownie, wielomian n-tego stopnia nie musi mieć N-1 punktów zwrotnych, może mieć mniej.
Uwaga Uwaga
ważne jest, aby uświadomić sobie różnicę między funkcjami parzystymi i nieparzystymi oraz wielomianami stopnia parzystego i nieparzystego. Każda funkcja, f(x), jest albo even if,
F(−x) = x,
dla wszystkich X w domenie f(x), lub nieparzyste if,
f(−x) = −x,
dla wszystkich X w domenie f(x), lub ani parzyste, ani nieparzyste, jeśli żadne z powyższych nie jest prawdą.
wielomian stopnia kth, p (x), mówi się, że ma stopień parzysty, jeśli K jest liczbą parzystą, a stopień nieparzysty, jeśli K jest liczbą nieparzystą. Pamiętaj, że nawet jeśli p (x) ma stopień parzysty, to niekoniecznie jest funkcją parzystą. Podobnie, jeśli p (x) ma nieparzysty stopień, niekoniecznie jest funkcją nieparzystą.
używamy również terminów parzystych i nieparzystych do opisu pierwiastków wielomianów. W szczególności wielomian p (x) ma pierwiastek X = a o wielokrotności K (tzn. x = A jest pierwiastkiem powtórzonym K razy), jeśli(x − A)K jest współczynnikiem p (x). Mówimy, że x = a ma parzystą wielokrotność, jeśli K jest liczbą parzystą i nieparzystą wielokrotność, jeśli K jest liczbą nieparzystą.
Domena i zakres
wszystkie wielomiany mają tę samą domenę, która składa się ze wszystkich liczb rzeczywistych. Na zakres wielomianów stopnia nieparzystego składają się również wszystkie liczby rzeczywiste. Zakres wielomianów parzystych stopni jest nieco bardziej skomplikowany i nie możemy jednoznacznie określić zakresu wszystkich wielomianów parzystych stopni. Jeśli współczynnik wiodący jest dodatni, funkcja rozszerzy się do+∞; natomiast jeśli współczynnik wiodący jest ujemny, rozszerzy się do -∞. Oznacza to, że wielomiany parzyste stopnia z dodatnim współczynnikiem wiodącym mają zakres, w którym ymax oznacza globalne maksimum, które osiąga funkcja. Ogólnie rzecz biorąc, nie jest możliwe analityczne określenie maksimów lub minimów wielomianów.
*****
w następnej sekcji poznasz dzielenie wielomianów, technikę stosowaną do znajdowania pierwiastków funkcji wielomianowych.
podział wielomianowy