Maximum Parsimony on Phylogenetic networks

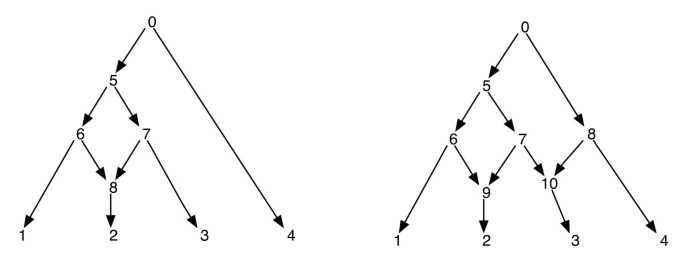
Rysunek przedstawia dwie sieci filogenetyczne; ta po lewej stronie ma tylko jeden wierzchołek siatkowaty, a ta po prawej ma dwa wierzchołki siatkowate, które są siostrzane dla siebie. Zauważ, że usunięcie krawędzi (7, 9) i (7, 10) z sieci po prawej stronie nie powoduje powstania drzewa, w którym wierzchołek 7 jest liściem. Pokazuje to, że usunięcie jednej przychodzącej krawędzi na wierzchołek siatki niekoniecznie powoduje powstanie drzewa z tym samym zestawem liści co sieć. Po zamówieniu i przed zamówieniem wierzchołków sieci po lewej stronie są 1, 2, 8, 6, 3, 7, 5, 4, 0 oraz 0, 5, 6, 1, 8, 2, 7, 3, 4 odpowiednio i dla sieci po prawej stronie są to 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 oraz 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 odpowiednio.

zanim przejdziemy do definicji problemów parsimony, poniżej znajduje się przydatna obserwacja. Dla sieci filogenetycznej n bez siatek siostrzanych, posiadającej wierzchołki siatkowe r i z zestawem liści X, oznaczamy T (N) jako zbiór wszystkich drzew zawartych w N. każde takie drzewo uzyskuje się przez następujące dwa kroki: (1) dla każdego wierzchołka siatkowego usuń jedną z przychodzących krawędzi, a następnie (2) dla każdego wierzchołka v indegree i outdegree 1, którego rodzicem jest u, a dzieckiem jest w, kurczymy krawędzie (U, v) i (v, w) w jedną krawędź (u, w). Warunek, że każda krawędź w N ma wierzchołek drzewa jako punkt końcowy i że każdy wierzchołek drzewa ma co najmniej jeden wierzchołek drzewa jako dziecko, zapewnia, że zbiór liści wynikowego drzewa jest taki sam jak w sieci. Stąd zbiór T (N ) zawiera dokładnie 2rfilogenetyczne drzewa, których zbiór liści jest dokładnie X.

Maksymalna Parsimonia

odsyłamy czytelników do ogólnego opisu idei parsimonii i do omówienia różnych algorytmów parsimonii. Zwrócono uwagę, że metoda parsimony dla drzew może zostać rozszerzona na sieci filogenetyczne. W serii prac, jedno takie kryterium parsimony jest definiowane przez znalezienie drzewa w sieci, który ma najlepszy wynik parsimonious, i skuteczne algorytmy do optymalizacji tego kryterium na danej sieci filogenetycznej zostały opracowane. Chociaż algorytmy te są pokazane, że działają dobrze w praktyce, mogą działać poprawnie tylko dla sieci filogenetycznych bez siatek siostrzanych, ponieważ łatwo jest szukać optymalnego drzewa w tych ograniczonych klasach sieci. W tej sekcji przedstawiamy alternatywną wersję problemu parsimonii, a w kolejnych sekcjach przedstawiamy rozwiązania heurystyczne optymalizujące wynik w dowolnej sieci filogenetycznej.

Let = {1, 2, …, n} oznacza zbiór listków danej sieci filogenetycznej N. funkcja λ: → {0, 1, …,| Σ / – 1} nazywa się funkcją przypisania stanu nad alfabetem Σ (zbiór niepustyczny) dla N. mówimy, że funkcja λ ^: V (N ) → { 0 , 1 , … , | Σ / – 1 } jest przedłużeniem λ NA N, jeśli zgadza się z λ na liściach N. Dla wierzchołka v W N nazywamy λ ^ (v) jako przypisanie λ ^ NA v. w pełni przypisana sieć to sieć, w której wszystkie wierzchołki mają etykiety od {0, 1,…, |Σ| – 1}. Niech C będzie macierzą kosztową, której pozycja C ij jest kosztem przekształcenia ze stanu i do stanu j wzdłuż dowolnej krawędzi w N. Jeśli E = (U, v) jest krawędzią w n, gdzie u jest rodzicem V, oznaczamy w e (λ) ^ = c I j, gdzie i = λ ^ (u) I j = λ ^ (v). Dla grafu G, niech E (G) oznacza zbiór krawędzi G. wtedy problem parsimonii jest zdefiniowany następująco.

Wejście:

kryterium Parsimonii: dla rozszerzenia λ ^ λ, niech

i

i

Wyjście: podane P ∈ {P1, P2}, znajdź λ ^, które minimalizuje P (λ ^).

zauważamy, że p 1 ( λ ^ ) jest wprowadzony w, A P 2 ( λ ^ ) jest definicją, której użyjemy w tym artykule. Bardziej ogólnym podejściem jest zminimalizowanie Q ( λ ^ ) = ∑ E ∈ E ( N ) d e ( w e ( λ ^ ) ) , gdzie d E jest nieujemną funkcją wagi na krawędziach N. na potrzeby tego artykułu ograniczamy się do P = P2, chociaż pierwsze z naszych podejść, rozwiązanie programowania dynamicznego ma również zastosowanie do p = Q.

algorytmy Parsimony w sieciach

przemierzające sieć filogenetyczną

w sieci, Przejście wierzchołka odnosi się do procesu odwiedzenia każdego wierzchołka, dokładnie raz, w sposób systematyczny. Takie trawersy są klasyfikowane według kolejności odwiedzania wierzchołków. Do opisania naszych algorytmów potrzebujemy dwóch typów trawersów wierzchołków sieci. Są one dobrze znane z drzew filogenetycznych i prezentujemy je tutaj dla sieci filogenetycznych. Algorytmy dla trawersów podane poniżej zaczynają się od dowolnego wierzchołka v w sieci. W tym artykule zawsze będziemy wykonywać trawersy z głównego wierzchołka sieci.

pre-order przemierzanie sieci filogenetycznej z wierzchołka v

1. odwiedź wierzchołek v.

2. rekurencyjnie wykonuj przemierzanie przed-order od każdego dziecka, które nie zostało jeszcze odwiedzone.

Post-order traversal sieci filogenetycznej z wierzchołka v

1. rekurencyjnie wykonuj Post-order traversal od każdego dziecka, które nie zostało jeszcze odwiedzone.

2. odwiedź wierzchołek v.

ponieważ sieć filogenetyczna jest DAG, takie trawersy odwiedzą wszystkie wierzchołki sieci dokładnie raz. (Zobacz więcej szczegółów na temat istnienia takich trawersów na dag). Na potrzeby niniejszego artykułu Zakładamy, że wierzchołki sieci są jednoznacznie oznaczone liczbami całkowitymi. Zauważ, że liście są już oznakowane z zestawu ; i tak używamy innych liczb całkowitych dla innych wierzchołków. Ilekroć wyciągane są wierzchołki potomne V, są one również ułożone w rosnącej kolejności ich oznaczeń całkowitych, a trawersy pre – i post-order są wykonywane w tej kolejności. Zapewni to, co następuje: jeśli wierzchołki v i v’ są takie, że nie ma skierowanej ścieżki między nimi, to wierzchołek v jest przemierzany przed wierzchołkiem v’ w pre-order wtedy i tylko wtedy, gdy wierzchołek v jest przemierzany przed wierzchołkiem v’ w post-order. Przykłady przedstawiono na rysunku 1. Z tą właściwością zauważamy, że trawersy przed i po rzędu z korzenia sieci filogenetycznej, każdy śledzi to samo drzewo, które nazywamy tutaj drzewem trawersowym.

Dynamic Programming solution

Programowanie dynamiczne służy do zapewnienia wydajnych rozwiązań w celu znalezienia dokładnego wyniku parsimony, gdy sieć jest drzewem filogenetycznym . W tej sekcji pokazujemy, że to samo podejście można uogólnić do sieci filogenetycznych. Algorytm sankoffa na drzewie trawersuje wierzchołki drzewa poprzez post-order, obliczając minimalne koszty każdego stanu na każdym wierzchołku od liści do korzenia, a następnie wybiera najlepsze przydziały na każdym wierzchołku, cofając się od korzenia do liści, przemierzając wierzchołki drzewa za pośrednictwem pre-order. Obie fazy są przedstawione dla sieci odpowiednio w algorytmach 1 i 2. Opisujemy je krótko poniżej. Można zauważyć, że jeśli sieć jest drzewem, to nasze algorytmy pasują do faz pre-order I post-order metody Sankoffa dla drzew.

biorąc pod uwagę sieć filogenetyczną N, z oznaczonymi wierzchołkami liści i z funkcją przyporządkowania Stanów λ nad alfabetem Σ, Przypisz każdemu wierzchołkowi V ∈ V Ilość S v (i) dla każdego i ∈ Σ. W drzewach filogenetycznych S v (i) oznacza minimalną sumę kosztów wszystkich zdarzeń od wierzchołka v do wszystkich liści osiągalnych od v, biorąc pod uwagę, że V jest przypisany stan i, a wszystkie wierzchołki potomne od v są przypisane do stanu. W sieciach nie ma prostego sposobu na obliczenie takiej ilości. Zamiast tego pozwalamy S v (i) być niższą granicą powyższego dokładnego wyniku i jest on obliczany podczas fazy przechodzenia po zamówieniu.

Faza poprzeczna: jeśli v jest liściem N, to S v (i) jest przypisane 0, jeśli obserwowany stan jest stanem i, a nieskończony w przeciwnym razie. Teraz wszystko, czego potrzebujemy, to relacja rekurencji do obliczenia S v (i) dla reszty wierzchołków. Dla każdego dziecka w od v mówimy, że w spełnia warunek poprzeczny względem V, lub po prostu warunek poprzeczny względem v w świetle obserwacji na początku tej sekcji, jeśli następujące:

1. (i)

   wierzchołek w jest wierzchołkiem siatkowatym i

2. (ii)

   Jeśli V’ jest nadrzędnym w innym niż v, to wierzchołek V musi być przechodził przed V’ w poprzecznym przejściu N.

definiujemy teraz rekurencyjnie dla każdej krawędzi (v, w),

dla drzewa filogenetycznego, s(v, w)(i) zawsze przyjmuje pierwszą z tych wielkości, a tym samym daje sumę kosztów substytucji wzdłuż krawędzi drzewa leżącego poniżej wierzchołka v, pod warunkiem, że wierzchołkowi v przypisany jest stan i. dla sieci filogenetycznych, w celu uwzględnienia kosztów substytucji wzdłuż krawędzi leżących poniżej wierzchołka siatkowatego w tylko jeden raz, gdy wierzchołkowi v przypisany jest stan i, pozwalamy 'rodzicowi’ v Z w w drzewo trawersowe uwzględnia wszystkie koszty substytucji wzdłuż wszystkich krawędzi leżących poniżej V. Z drugiej strony, jeśli v nie jest rodzicem w w drzewie trawersowym, s (v, w) (i) oznacza po prostu koszt substytucji ze stanu i na wierzchołku v do innego stanu na w, który jest najtańszy.

następnie definiujemy

gdzie suma biegnie dla wszystkich potomnych(Ren) wierzchołków(s) W z v. Jak wspomniano wcześniej, w drzewach filogenetycznych, S v (i) oznacza minimalną możliwą sumę kosztów substytucji wzdłuż wszystkich krawędzi od wierzchołka v do wszystkich liści, które są osiągalne od v, biorąc pod uwagę, że V jest przypisany stan i, a wszystkie wierzchołki osiągalne od v są przypisane stan.

w sieciach filogenetycznych, podczas obliczania s(v, w)(i), gdzie w jest wierzchołkiem siatkowatym, takim, że (v, w) nie jest krawędzią drzewa poprzecznego, nie ma wcześniejszej wiedzy o stanie, który zostanie później przypisany wierzchołkowi siatkowatemu w. Tak więc s(v, w) (i) może być dolną granicą krawędzi sieci leżących poniżej wierzchołka v, jeśli wierzchołkowi v przypisany jest stan i. rozumowanie tego polega na tym, że S(v, w) (i) jest kosztem substytucji ze stanu i na wierzchołku v do innego stanu na w, który jest najtańszy, zamiast kosztu substytucji ze stanu i na v do stanu na w, który zostanie później przypisany. Ponieważ definicja S v (i) zależy od definicji S(v, w) (I) i są definiowane rekurencyjnie, obserwujemy następujące: S v (i) jest niższą granicą sumy kosztów substytucji wzdłuż krawędzi sieci, które są osiągalne z wierzchołka v, pod warunkiem, że V jest przypisany stan i, a wszystkim wierzchołkom drzewa potomnego jest przypisany unikalny stan, a wierzchołkom siatkowatym są przypisane dwa stany, które niekoniecznie są takie same. Przypisane Stany wierzchołka siatkowatego przyczyniają się do konfliktu, jeśli Stany nie są takie same. Załóżmy, że stan i jest przypisany do wierzchołka głównego r, a wszystkim wierzchołkom drzewa przypisany jest unikalny stan, podczas gdy wierzchołkom siatkowatym przypisane są dwa stany. Następnie koszt S r (i) oznacza minimalną możliwą sumę kosztów substytucji wzdłuż wszystkich krawędzi drzewa trawersowego z jednym ze Stanów przypisanych do wierzchołków siateczkowych, plus sumę kosztów substytucji wzdłuż pozostałych krawędzi siateczkowych z alternatywnym stanem przypisania na wierzchołkach siateczkowych. Ponieważ szukamy przypisania na wierzchołkach sieci bez konfliktów w wierzchołkach siatkowych, S r (i) jest niższą granicą kosztu takiego przypisania, gdzie wierzchołek główny jest przypisany i, a wszystkie wierzchołki są przypisane z unikalnym przypisaniem.

podczas tej fazy przechowujemy również stany

aby móc cofnąć stan w, który osiąga ilość S(v, w)(i) podczas fazy zamówienia wstępnego. Patrz Algorytm 1.

pre-order traversal phase: najpierw wybieramy minimum

gdzie r jest wierzchołkiem głównym i przypisujemy stan, który osiąga minimum w wierzchołku głównym, tzn., niech λ ^ (r) = i R takie, że S r (i r) = S. dla każdego innego wierzchołka w, który nie jest wierzchołkiem siatkowatym, którego nadrzędny v jest już przypisany do stanu i, przypisujemy stan t(v, w)(i). Dla wierzchołka siatkowatego w, którego wierzchołkami nadrzędnymi są v I v’, Załóżmy, że v i v 'są przypisane odpowiednio do stanów i I i’ podczas przechodzenia przez kolejność wstępną. Możliwe Stany j = t(v, w) (i) I j’ = t(v’, w) (i’) w, które osiągają odpowiednio s(v, w) (I) I s(v’, w) (i’), nie muszą być takie same. Innymi słowy, możliwe jest, że j ≠ j’. W tym przypadku mamy konflikt na reticulate vertex w. tak więc technika programowania dynamicznego nie daje rozszerzenia dla λ, którego wynik parsimony wynosi S. w tym przypadku po prostu wybieramy pomiędzy J I j’ dla λ(w), zgodnie z którym z wierzchołków między v i v’ jest przemierzany jako pierwszy w pre-order. Tak więc, jeśli wierzchołek w spełnia warunek przejścia względem v, mamy λ ^ (w) =j.

Po zakończeniu fazy pre-order, możemy uzyskać wynik odpowiadający rozszerzeniu λ ^, ustawiając najpierw S '= S i aktualizując s ’ przy każdym wierzchołku w następująco: Górny wynik graniczny S „jest aktualizowany odpowiadając przypisaniu j na wierzchołku w jako S” – c i ” j „+c i ” j . Patrz Algorytm 2. Rysunek 2 przedstawia przykład działania algorytmu w sieci. Ponieważ S r (i) jest dolną granicą przyporządkowania optimum, gdzie wierzchołek główny jest przypisany i, a wszystkie wierzchołki są przypisane z unikalnym przyporządkowaniem, a ponieważ S = min I S R (i), wnioskujemy, że s jest dolną granicą optimum, które chcemy znaleźć. Zobacz Lemma 1, Aby uzyskać formalny dowód.

dynamiczne rozwiązanie programistyczne. Dynamic programming solution applied to a phylogenetic network. Stany to 0, 1 i 2. Zastosowana macierz kosztów ma wszystkie 1s z wyjątkiem elementów przekątnych, które są wszystkimi 0s. tabele pokazane na każdym wierzchołku v są kosztami, S v (i) (drugi wiersz) każdego stanu, i (pierwszy wiersz), które są obliczane podczas przechodzenia po zamówieniu. Na wierzchołkach pokazane są również stany dziecka w, a mianowicie t (v, w) (i) (trzeci rząd), które odpowiadają kosztom w drugim rzędzie; gdy dla wierzchołka jest dwoje dzieci, wpisy w trzecim rzędzie są reprezentowane jako para Stanów odpowiednio lewego dziecka i prawego dziecka. Każda krawędź(v, w) jest oznaczona symbolem S(v, w) (i) dla każdego stanu i. podczas przechodzenia w przedsprzedaży wybierane są Stany dla każdego wierzchołka (pokazane pogrubioną czcionką). Koszt 2 podświetlony pogrubioną czcionką na wierzchołku głównym daje dolną granicę, S. stan przypisany na każdym wierzchołku jest podświetlony pogrubioną czcionką. Algorytm znajduje w sumie trzy podstawienia (wyróżnione pogrubionymi krawędziami). Wynika to z faktu, że Stany przypisane na wierzchołkach nadrzędnych wierzchołka siatkowatego dają sprzeczne przydziały odpowiednio 1 i 2, z których stan 1 jest przypisany na wierzchołku siatkowatego. Tak więc z dodatkowym kosztem 1, otrzymujemy wynik 3 (górna granica optymalnego wyniku) jako wynik parsimony odpowiadający pokazanemu zadaniu. Należy zauważyć, że optymalny wynik parsimony w sieci wynosi 2 (równy dolnej granicy), który można znaleźć poprzez wyczerpujące wyszukiwanie i można go zrealizować, zmieniając przypisanie z 1 na 2 dla lewego rodzica wierzchołka siatkowatego i od 1 do 2 dla wierzchołka siatkowatego. Tak więc dolna granica pasuje do optymalnego wyniku, chociaż przypisanie odpowiadające dolnej granicy nie jest bezkonfliktowe i nie jest takie samo jak przypisanie odpowiadające optymalnemu.

Ilość S jest dolną granicą optymalnego wyniku parsimonii w sieci N.

dowód. W konstrukcji S mamy

s= ∑ ( v, w ) ∈ E ( N ) : W jest wierzchołkiem drzewa c λ ^ ( v), λ ^ ( w ) + ∑ ( v , w), (v’, w ) ∈ E ( N),

(3)

gdzie drugie Summit jest dla wierzchołka siatkowatego w z rodzicami są v i v’, takie, że V spełnia warunek przejścia w.R.T. w. zatem koszt c λ ^ ( v ) , λ ^ ( w ) jest kosztem substytucji ze stanu przypisanego λ ^ ( V ) W V do stanu λ ^ ( w ) w. Z drugiej strony, koszt c λ ^ ( v ’) , t ( V ’, w ) ( λ ^ ( v ’) ) jest kosztem substytucji ze stanu przypisanego λ ^ ( V ) W v do stanu T ( V ’, w ) ( λ ^ ( v ’) ) W w. Należy zauważyć , że stan T ( V’, w ) ( λ ^ ( v ’ ) ) niekoniecznie jest taki sam jak stan λ ^ ( w), A S jest minimalnym spośród wszystkich przypisań, które mogą powodować konflikty na wierzchołkach siatkowatych.

przypuśćmy, że s ^ jest optymalnym wynikiem parsimonii na N z funkcją μ: V (N) → {0, 1, …,| Σ/ – 1} jako rozszerzenie λ mamy

s ^ = ∑ ( v , w ) ∈ E (N ) : w jest wierzchołkiem drzewa c μ ( v ) , μ ( w ) + ∑ ( v , w ) , ( v ’, w ) ∈ E ( N ) ,

(4)

gdzie w drugim sumowaniu w jest wierzchołkiem siatkowatym z rodzicami v i v’. Ponieważ μ jest przyporządkowaniem bezkonfliktowym, które jest zawarte w zbiorze wszystkich przydziałów, wśród których S jest minimalnym (porównaj równanie (3) i (4)), mamy s≤ s ^ . □

teraz dla złożoności algorytmu. Załóżmy, że sieć N ma N liści i R wierzchołków siatkowych. Wtedy liczba wierzchołków W N wynosi 2 (n + r) -1. Dla każdego wierzchołka v i dla każdego stanu i, ilość s można obliczyć w czasie O (k2), gdzie k = / Σ/. Krok przechodzenia w przedsprzedaży polega na znalezieniu s W O (k) złożoności i przypisaniu najlepszych stanów dla każdego wierzchołka. Ponadto, naprawienie sprzecznych Stanów siateczkowych wierzchołków zajmuje Czas O (r). Tak więc złożoność algorytmu (przedstawionego tutaj)do znalezienia dolnej i górnej granicy wynosi O((n + r)k2). Alternatywną górną krawędź można uzyskać W O (nk2), po prostu przypisując podczas fazy trawersowania po zamówieniu, dla każdego wierzchołka siatkowatego stan, który występuje maksymalną liczbę razy na liściach osiągalnych z odpowiedniego wierzchołka siatkowatego; i przechodząc przez znalezienie S v (i) dla pozostałych wierzchołków. Dokładne optimum można również uzyskać, ograniczając możliwe Stany do pojedynczego stanu dla każdego wierzchołka siatkowatego, uruchamiając algorytm programowania dynamicznego dla każdej z kombinacji Stanów kr dla wierzchołków siatkowatego i wybierając minimum spośród wszystkich z nich. Złożoność czasowa tego procesu wynosi O (nkr+2).

algorytm 1 faza przechodzenia po zleceniu: Oblicz koszt każdego stanu na każdym wierzchołku

1. 1:

   Wejście: sieć N i obserwowane Stany Z Σ na liściach N, tj. funkcja przypisania stanu λ nad alfabetem Σ Dla n.

2. 2:

   dla każdego liścia v, niech S v (i) = 0, jeśli λ(v) = i i ∞ w przeciwnym razie.

3. 3:

   powtórz po kolei dla każdego w wierzchołku wewnętrznym (korzeń, wierzchołek drzewa wewnętrznego lub wierzchołek siatkowaty) v W N: Dla każdego stanu i Oblicz S v (i) podane w (1) i t(v, w)(i) dla każdego dziecka w od v, podane w (2).

4. 4:

   wyjście: {(S v (i),): v ∈ V (N), i ∈ Σ}.

minimalizowanie liczby mutacji w sieci filogenetycznej

algorytm Fitcha liczy liczbę zmian w rozwidlającym się drzewie filogenetycznym dla dowolnego zbioru znaków, gdzie stany mogą zmieniać się z dowolnego stanu na dowolny inny. Tak więc macierz kosztów jest taka, że jej elementy przekątne są wszystkimi zerami, a elementy poza przekątnymi są jedynkami. W tej sekcji pokazujemy, jak algorytm Fitcha rozszerza się na znajdowanie górnych i dolnych granic liczby zmian ewolucyjnych w danej sieci filogenetycznej. Po pierwsze, pokazujemy, że algorytm Fitcha można rozszerzyć, aby dać górną granicę dla optymalnego wyniku parsimony. Podobnie jak poprzednio, fazy Post-order i pre-order są podane w algorytmach 3 i 4 poniżej. Przykładowy przebieg algorytmu znajduje się na rysunku 3.

Rozwiązanie typu Fitch stosowane do tej samej sieci filogenetycznej i danych liści na rysunku 2. Każdy wierzchołek ma przypisany zestaw wszystkich możliwych stanów, wraz z wynikiem, gdy wierzchołki sieci są przemierzane po kolei. Wynik u korzenia daje górną granicę dla optymalnego wyniku. Przydziały stanu są podawane podczas fazy przedsprzedażowej, a liczba zastępstw odpowiada punktacji u podstaw.

: Oblicz dolną i górną granicę optimum i odpowiadającą jej górną granicę

1. 1:

   Input: {(S v (i),): v ∈ V (N), i ∈ Σ}.

2. 2:

   Let s = min i S r (i), gdzie r jest wierzchołkiem korzenia i let λ ^ ( r) =arg min i S r ( i).

3. 3:

   Let s’ = S

4. 4:

   dla każdego wierzchołka w w pre-porządku, którego wierzchołek nadrzędny v bezpośrednio poprzedza w w pre-porządku , niech λ ^ ( ω ) = T v , w ( i), gdzie i= λ ^ ( v ) .

5. 5:

   odwiedź każdy siatkowaty wierzchołek w z rodzicami v i v 'tak, że w spełnia warunek przejścia względem v , Z i= λ ^ ( v), i '= λ ^ ( v’), j '= t ( v’, w ) ( I ) i zaktualizuj S’ następująco:

   s '← S ’- c i ’ j '+ c I ’ j .
6. 6:

   wyjście: (dolna granica, górna granica) = (S, S’); rozszerzenie odpowiadające górnej granicy s ’ : λ ^ .

algorytm 3: Oblicz optymalne

1. 1:

   Wejście: Sieć filogenetyczna N i funkcja przypisania stanu λ nad alfabetem Σ Dla n.

2. 2:

   dla każdego liścia v Z N otrzymujemy a(v) = {λ(v)}, zbiór singletonów zawierający obserwowany stan na liściu.

3. 3:

   Set UB = 0.

4. 4:

   Recurse using post-order: for a vertex v of T with children W1 and W2, let and If the vertex v has a single child w, then

and

A ( v ) = a ( w 1 ) ∩ A ( W 2 ) if a ( w 1 ) ∩ a ( w 2 ) ≠ 0 ; a ( w 1 ) ∪ a ( w 2 ) otherwise .

ub← ub jeśli A ( v 1 ) ∩ A ( v 2 ) ≠ 0 ; u b + 1 w przeciwnym razie .

A ( v ) = a ( w),

U B .

5: ({A(v): V ∈ V (N)}, UB)

ponieważ faza przejścia pre-order daje bezkonfliktowe przypisanie na wierzchołkach, UB jest górną granicą. Jest to szczególny przypadek algorytmu dynamicznego przedstawionego dla macierzy kosztów ogólnych. Załóżmy, że ograniczymy N do sieci filogenetycznej bez siatek siostrzanych, wtedy każde rozwiązanie Fitcha na dowolnym drzewie T W T ( N ) tworzy dolną granicę dla optymalnego wyniku na sieciach; a dodanie kosztu na krawędziach nie w T daje górną krawędź dla optymalnego wyniku. Tak więc możliwe jest obliczenie dolnej granicy dla liczenia liczby zmian postaci tylko dla sieci filogenetycznych bez siatek siostrzanych, gdzie łatwo jest znaleźć drzewo w T (N).

algorytm 4 Faza przechodzenia: przypisanie Stanów

1. 1:

   Wejście: drzewo filogenetyczne N I ({A (v): v ∈ V (N)}, UB).

2. 2:

   dla każdego wierzchołka v w drzewie, który nie jest jeszcze przypisany, algorytm oblicza λ ^ (v) w następujący sposób: Dla pierwiastka r, λ ^ (r) = σ, gdzie σ jest arbitralnym elementem A (r). Przypisz rekurencyjnie poprzez kolejność wstępną: dla wierzchołka v, któremu przypisano rodzica u,

   λ ^ ( v ) = λ ^ ( u), jeśli λ ^ ( u ) ∈ a ( v ) ; σ ∈ a ( V ) w przeciwnym razie .
3. 3:

   ustalanie wyniku: dla każdego wierzchołka V, jeśli u’ nie jest rodzicem w przedsprzedaży, a jeśli λ ^ ( u ’) ∈A ( v ) , ale λ ^ ( u ’ ) ≠ λ ^ ( v ) , to zwiększ UB o 1.

4. 4:

   wyjście: UB i funkcja rozszerzenia λ ^ od λ.