BasicsEdit
Po pierwsze, niektóre słownictwo:
| aktywacja | = stan wartość neuronu. Dla neuronów binarnych jest to zwykle 0 / 1 lub +1 / -1. |
| CAM | = zawartość pamięci adresowalnej. Przywołanie pamięci przez częściowy wzorzec zamiast adresu pamięci. |
| konwergencja | = stabilizacja wzorca aktywacji w sieci. W SL konwergencja oznacza stabilizację wag &, a nie aktywacje. |
| Nazywany również analizą (w teorii wzorców), czyli wnioskowaniem. | |
| energia | = makroskopowa wielkość opisująca wzorzec aktywacji w sieci. (patrz poniżej) |
| uogólnienie | = zachowywanie się dokładnie na wcześniej nie napotkanych wejściach |
| generatywne | = zadanie wyobraźni Maszyny i przypomnienia. czasami nazywane syntezą (w teorii wzorców), mimikrą lub głębokimi podróbkami. |
| wnioskowanie | Faza „run” (w przeciwieństwie do treningu). Podczas wnioskowania sieć wykonuje zadanie, do którego jest przeszkolona-rozpoznawanie wzorca (SL) lub tworzenie wzorca (UL). Zwykle wnioskowanie sprowadza się do gradientu funkcji energetycznej. W przeciwieństwie do SL, gradientowe zejście występuje podczas treningu, a nie wnioskowania. |
| widzenie maszynowe | = uczenie maszynowe na obrazach. |
| NLP | = przetwarzanie języka naturalnego. Uczenie maszynowe ludzkich języków. |
| wzorzec | = aktywacje sieciowe, które mają w pewnym sensie wewnętrzny porządek lub które można opisać bardziej zwięźle za pomocą funkcji w aktywacjach. Na przykład wzorzec pikseli zera, niezależnie od tego, czy jest on podany jako dane, czy wyobrażony przez sieć, ma funkcję, którą można opisać jako pojedynczą pętlę. Funkcje są zakodowane w ukrytych neuronach. |
| szkolenie | Faza uczenia się. Tutaj sieć dostosowuje swoje wagi &, aby uczyć się z wejść. |
zadania
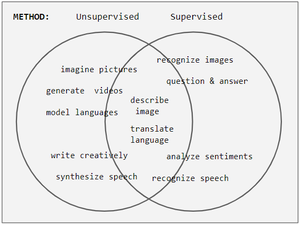
metody UL zwykle przygotowują sieć do zadań generatywnych zamiast rozpoznawania, ale grupowanie Zadań jako nadzorowane lub nie może być mgliste. Na przykład rozpoznawanie pisma zaczęło się w latach 80. jako SL. Następnie w 2007 r.UL jest używany do przygotowania sieci dla SL. Obecnie SL odzyskało pozycję lepszej metody.
Szkolenie
podczas fazy uczenia się sieć nienadzorowana próbuje naśladować dane, które otrzymuje i wykorzystuje błąd w swoim naśladowanym wyjściu, aby się poprawić (np. jego wag &). Przypomina to zachowanie mimiczne dzieci, gdy uczą się języka. Czasami błąd jest wyrażany jako niskie prawdopodobieństwo wystąpienia błędnego wyjścia lub może być wyrażany jako niestabilny stan wysokiej energii w sieci.
Energia
funkcja energetyczna jest makroskopową miarą stanu sieci. Ta analogia z fizyką jest zainspirowana analizą energii makroskopowej gazu przez Ludwiga Boltzmanna z mikroskopowego prawdopodobieństwa ruchu cząstek p ∝ {\displaystyle \propto}

eE/kT, gdzie k to stała Boltzmanna, A T to Temperatura. W sieci RBM relacja jest p = E-E / Z, gdzie p & e różni się w zależności od każdego możliwego wzoru aktywacji i Z = ∑ A l l P A t T e R n s {\displaystyle \sum _{AllPatterns}}

E-E(wzór). Dokładniej mówiąc, p (A) = e-E (A) / Z, gdzie A jest wzorcem aktywacji wszystkich neuronów (widocznych i ukrytych). Stąd też wczesne sieci neuronowe noszą nazwę Maszyny Boltzmanna. Paul Smolensky nazywa-e harmonia. Sieć szuka niskiej energii, która jest wysoka Harmonia.
Sieci
| Hopfield | Boltzmann | RBM | Helmholtz | Autoencoder | VAE |
|---|---|---|---|---|---|

|
 |
 restricted Boltzmann machine
|
 |
 autoencoder
|
 zmienny autoencoder
|
Boltzmann i Helmholtz pojawili się przed formułowaniem sieci neuronowych, ale sieci te zapożyczyły się z ich analiz, więc sieci te noszą swoje nazwy. Hopfield jednak bezpośrednio przyczynił się do UL.
IntermediateEdit
tutaj dystrybucje p(x) i q(x) będą skracane do p i q.
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) AI winter I |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolution neural network. Jest używany głównie w SL, ale zasługuje na wzmiankę tutaj. |
| 1982 | jest odmianą sieci Hopfield opisaną jako CAMs and classifiers przez Johna Hopfielda. |
| 1983 | Ising wariant Maszyny Boltzmanna z neuronami probabilistycznymi opisany przez Hintona& Sejnowski podążający za Sheringtonem & praca. |
| 1986 | Paul Smolensky publikuje teorię harmonii, która jest RBM z praktycznie tą samą funkcją energetyczną Boltzmanna. Smolensky nie dał praktycznego programu szkolenia. Hinton w połowie lat 2000 |
| 1995 | Schmidthuber wprowadza neuron LSTM dla języków. |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) AI winter II |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Some more vocabulary:
| prawdopodobieństwo | |
| CDF | = cumulative distribution function. Całka z pdf. Prawdopodobieństwo zbliżenia się do 3 to pole pod krzywą między 2.9 A 3.1. |
| rozbieżność kontrastowa | = metoda uczenia się, w której obniża się energię na wzorce treningowe i podnosi energię na niechciane wzorce poza zestawem treningowym. To bardzo różni się od KL-divergence, ale ma podobne sformułowanie. |
| wartość oczekiwana | = E(x) = ∑ x {\displaystyle \sum _{x}}
 x * p(x). Jest to wartość średnia lub średnia. Dla ciągłego wejścia x zastąp sumację całką. |
| zmienna utajona | = nieobserwowana ilość, która pomaga wyjaśnić obserwowane dane. na przykład zakażenie grypą (niezauważone) może wyjaśnić, dlaczego osoba kicha (obserwowane). W probabilistycznych sieciach neuronowych Ukryte neurony działają jako zmienne utajone, choć ich utajona interpretacja nie jest jednoznacznie znana. |
| = funkcja gęstości prawdopodobieństwa. Prawdopodobieństwo, że zmienna losowa przyjmuje określoną wartość. Dla ciągłego pdf, p (3) = 1/2 może nadal oznaczać, że istnieje prawie zerowa szansa na osiągnięcie tej dokładnej wartości 3. Racjonalizujemy to z cdf. | |
| stochastyczny | = zachowuje się zgodnie z dobrze opisanym wzorem gęstości prawdopodobieństwa. |
| Thermodynamics | |
| Boltzmann distribution | = Gibbs distribution. p ∝ {\displaystyle \propto }
 eE/kT |
| entropy | = expected information = ∑ x {\displaystyle \sum _{x}}
 p * log p |
| Gibbs free energy | = thermodynamic potential. Jest to maksymalna odwracalna praca, która może być wykonywana przez system cieplny przy stałej temperaturze i ciśnieniu. energia swobodna G=ciepło – temperatura * Entropia |
| informacja | = ilość informacji wiadomości x=- log p(x) |
| KLD | = Entropia względna. Dla sieci probabilistycznych jest to analogia błędu pomiędzy wejściem &. Dywergencja Kullbacka-Lieblera (KLD) mierzy odchylenie entropii 1 rozkładu od innego rozkładu. KLD (p, q) = ∑ x {\displaystyle \sum _{x}}
 p * log( P / q ). Zazwyczaj p odzwierciedla dane wejściowe, q odzwierciedla interpretację sieci, a KLD odzwierciedla różnicę między nimi. |
porównanie sieci
| Hopfield | Boltzmann | RBM | Helmholtz | autoencoder | VAE | |
|---|---|---|---|---|---|---|
| zastosowanie& notables | cam, problem ze sprzedawcą w podróży | cam. Swoboda połączeń sprawia, że sieć ta jest trudna do analizy. | rozpoznawanie wzorców (MNIST, rozpoznawanie mowy) | wyobraźnia, mimika | język: kreatywne pisanie, tłumaczenie. Wizja: Ulepszanie rozmytych obrazów | generowanie realistycznych danych |
| neuron | deterministyczny stan binarny. Aktywacja = { 0 (lub -1) jeśli X jest ujemne, 1 w przeciwnym razie } | stochastyczny binarny neuron Hopfielda | stochastyczny binarny. Rozszerzony do wartości rzeczywistej W połowie lat 2000 | binarny, sigmoid | język: LSTM. wizja: lokalne pola wrażliwe. zazwyczaj realnie ceniona aktywacja relu. | |
| połączenia | 1-warstwowe z symetrycznymi obciążnikami. Brak powiązań między sobą. | 2-warstwowe. 1-Ukryty & 1-widoczny. wagi symetryczne. | 2-warstwowe. wagi symetryczne. brak połączeń bocznych w warstwie. | 3-warstwowe: wagi asymetryczne. 2 sieci połączone w 1. | 3-warstwowe. Wejście jest uważane za warstwę, mimo że nie ma przychodzących wag. powtarzające się warstwy dla NLP. feedforward sploty dla wizji. wejście & wyjście ma taką samą liczbę neuronów. | 3-warstwowe: wejście, koder, dekoder samplera dystrybucji. próbnik nie jest uważany za warstwę (e) |
energia jest podana przez miarę prawdopodobieństwa Gibbsa : E = − 1 2 ∑ i , j w I J s I S J + ∑ i θ i s i {\displaystyle E=-{\frac {1}{2}}\sum _{I,j}{w_{IJ}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}}
 |
← same | minimalizuj dywergencję KL | wnioskowanie jest tylko feed-forward. poprzednie sieci UL przebiegały do przodu i do tyłu | Minimalizuj błąd = reconstruction error – KLD | ||
| szkolenie | Δwij = si*SJ, dla +1/-1 neuronu | Δwij = e*(pij – p ’ IJ). Wynika to z minimalizacji KLD. e = wskaźnik uczenia się, P’ = przewidywany i P = rzeczywisty rozkład. | rozbieżność kontrastowa w próbkowaniu Gibbsa | wake-sleep 2 Phase training | back propagate the reconstruction error | reparameterize hidden state for backprop |
| Siła | przypomina układy fizyczne, więc dziedziczy ich równania | <— to samo. Ukryte neurony działają jako wewnętrzna reprezentacja świata zewnętrznego | szybszy, bardziej praktyczny schemat szkolenia niż Maszyny Boltzmanna | łagodnie anatomiczny. analizowany z teorią informacji & mechanika statystyczna | ||
| słabość | hopfield | trudne do trenowania ze względu na powiązania boczne | RBM | Helmholtz |
określone sieci
tutaj podkreślamy niektóre cechy każdej sieci. Ferromagnetyzm zainspirował sieci Hopfield, Maszyny Boltzmann i kms. Neuron odpowiada domenie żelaza z binarnymi momentami magnetycznymi w górę i w dół, a połączenia neuronowe odpowiadają wpływowi domeny na siebie nawzajem. Połączenia symetryczne umożliwiają globalne formułowanie energii. Podczas wnioskowania sieć aktualizuje każdy stan za pomocą standardowej funkcji kroku aktywacji. Symetryczne wagi gwarantują zbieżność do stabilnego wzoru aktywacji.
sieci Hopfielda są używane jako kamery i mają gwarancję, że zadowoli się pewnym wzorem. Bez symetrycznych wag sieć jest bardzo trudna do analizy. Dzięki odpowiedniej funkcji energetycznej sieć będzie się zbiegać.
maszyny Boltzmanna to stochastyczne sieci Hopfielda. Ich wartość stanu jest pobierana z tego pliku pdf w następujący sposób: Załóżmy, że neuron binarny uruchamia się z prawdopodobieństwem Bernoulliego p(1) = 1/3 i spoczywa na p(0) = 2/3. Jedną próbkę z niej pobiera się przez pobranie równomiernie rozłożonej losowej liczby y i podłączenie jej do odwróconej funkcji rozkładu kumulacyjnego, która w tym przypadku jest funkcją stopniową progowaną w 2/3. Funkcja odwrotna = { 0 if X <=2/3, 1 if x > 2/3 }
maszyny Helmholtza są wczesnymi inspiracjami dla wariacyjnych koderów samochodowych. To 2 sieci połączone w jeden-do przodu wagi działa rozpoznawanie i do tyłu wagi realizuje wyobraźnię. Jest to prawdopodobnie pierwsza sieć, która robi obie te rzeczy. Helmholtz nie pracował w uczeniu maszynowym, ale zainspirował pogląd „silnika wnioskowania statystycznego, którego funkcją jest wnioskowanie prawdopodobnych przyczyn wejścia SENSORYCZNEGO” (3). stochastyczny neuron binarny generuje prawdopodobieństwo, że jego stan wynosi 0 LUB 1. Wprowadzanie danych zwykle nie jest uważane za warstwę, ale w trybie generowania Maszyny Helmholtza, Warstwa danych otrzymuje dane z warstwy środkowej ma oddzielne wagi do tego celu, więc jest uważana za warstwę. Stąd ta sieć ma 3 warstwy.
variational Autoencoder (Vae) są inspirowane maszynami Helmholtza i łączą sieć prawdopodobieństwa z sieciami neuronowymi. Autoencoder to trójwarstwowa sieć krzywkowa, w której warstwa środkowa ma być jakąś wewnętrzną reprezentacją wzorców wejściowych. Wagi mają nazwę phi & theta, a nie W I V jak w Helmholtzu-różnica kosmetyczna. Sieć neuronowa kodera jest rozkładem prawdopodobieństwa qφ (z|x), a sieć dekodera jest pθ(x / z). Te 2 Sieci tutaj mogą być w pełni połączone lub korzystać z innego systemu NN.
Hebbian Learning, ART, SOM
klasycznym przykładem uczenia się bez nadzoru w badaniu sieci neuronowych jest zasada Donalda Hebba, czyli neurony, które odpalają się razem. W nauczaniu Hebbiańskim połączenie jest wzmacniane niezależnie od błędu, ale jest wyłącznie funkcją zbieżności potencjałów działania między dwoma neuronami. Podobna wersja modyfikująca masy synaptyczne uwzględnia czas pomiędzy potencjałami działania (plastyczność zależna od spike-timing lub STDP). Uczenie się Hebbian było hipotezą leżącą u podstaw szeregu funkcji poznawczych, takich jak rozpoznawanie wzorców i uczenie się empiryczne.
wśród modeli sieci neuronowych, samoorganizująca się Mapa (SOM) i adaptacyjna teoria rezonansu (ART) są powszechnie stosowane w algorytmach uczenia się bez nadzoru. SOM jest organizacją topograficzną, w której pobliskie lokalizacje na mapie reprezentują obiekty o podobnych właściwościach. MODEL ART pozwala na zmianę liczby klastrów w zależności od rozmiaru problemu i pozwala użytkownikowi kontrolować stopień podobieństwa między członkami tych samych klastrów za pomocą zdefiniowanej przez użytkownika stałej zwanej parametrem czujności. Sieci artystyczne są używane do wielu zadań rozpoznawania wzorców, takich jak automatyczne rozpoznawanie celów i przetwarzanie sygnałów sejsmicznych.