Herezja występuje na różnych poziomach. Dla współczesnego intelektualisty najniższy poziom herezji może dotyczyć polityki lub ekonomii-obszarów myśli, w których można mieć niekonwencjonalne pomysły bez wykluczania z grzecznego Towarzystwa. Wyższy poziom herezji może dotyczyć religii lub nauki-nie zgadzam się z ortodoksyjnymi założeniami tutaj, a będziesz postrzegany jako całkiem-możliwe-szalony. Najwyższym poziomem herezji we współczesnym świecie jest herezja matematyczna. Niezgoda z ortodoksją matematyczną jest synonimem ” bycia pełnowymiarową korbą.”Po prostu nie wolno Ci wątpić w pewne idee w matematyce, nie będąc potępionym jako intelektualny trędowaty.
Niestety, jak w przypadku każdej innej dziedziny myślenia, istnieje odwrotna zależność między „akceptowalnością niezgody” a „prawdopodobieństwem błędu.”Im bardziej tabu jest kwestionowanie założeń, tym bardziej prawdopodobne jest, że upadnie pod kontrolą. Teologowie mogą być w stanie tolerować niezgodę na temat właściwości Boga, ale nie mogą tolerować niezgody na temat istnienia Boga. Jego istnienie jest zbyt fundamentalne, by je zrewidować. Jeśli Bóg nie istnieje, cała teoretyczna struktura zbudowana na tym założeniu ulega zniszczeniu.
tak jest z matematyką. Kilka fundamentalnych założeń nie może być kwestionowanych i dlatego przekształciło się w dogmat, co czyni ten artykuł matematyczną herezją.
zbadałem podstawy Standardowej geometrii i znalazłem dwa błędy – jeden logiczny, drugi metafizyczny. Ten artykuł skupi się na metafizyce. Istotne obiekty opisane przez matematyków nie istnieją. Zatem wszelkie wnioski, które wynikają z istnienia tych obiektów, są prawdopodobnie błędne.
w tym przypadku powszechnie przyjęte twierdzenie, że „Pi jest liczbą irracjonalną, transcendentalną, której wielkości nie można wyrazić skończonym rozszerzeniem dziesiętnym” jest fałszywe z powodu błędu metafizycznego.
Pi jest liczbą wymierną ze skończonym rozszerzeniem dziesiętnym. Ten pomysł, który na początku może wydawać się niepojęty, okaże się przytłaczająco rozsądny pod koniec tego artykułu.
(dla reszty tego artykułu, będę skrótem „Pi jest liczbą wymierną ze skończonym rozszerzeniem dziesiętnym” jako „Pi jest liczbą skończoną” lub prościej, „Pi jest skończona.”)
Na kształtach
moje twierdzenia są proste i zachowują podstawową intuicję geometryczną. Na przykład jest to „okrąg”:

To jest”linia”:

i są to „punkty”:

Jeśli uważasz, że te obiekty to rzeczywiście okręgi, linie i punkty, to też wierzysz, że pi jest skończone. Widzisz, matematycy nie wierzą, że te obiekty kwalifikują się jako” linie „lub” punkty.”W ich umysłach linie i punkty nie mogą być widoczne, a w rzeczywistości powiedzieliby, że powyższe „linie i punkty” są jedynie niedoskonałymi przybliżeniami linii i punktów.
aby zrozumieć dlaczego, musimy zadać zestaw pytań, na które ludzie zakładają, że odpowiedzi zostały już wyjaśnione. Są to pytania, które są podobno tak oczywiste, że nie warto ich zadawać. A jednak, kiedy pytamy ich matematyków, otrzymujemy wątpliwe odpowiedzi. Pytania typu:
Co to jest „kształt”?
Co to jest „linia”?
Co to jest „punkt”?
Co to jest „krąg”?
Co to jest „odległość”?
Zadaj te pytania przeciętnemu intelektualiście, a prawdopodobnie będą z Ciebie szydzić, ponieważ zakładają: „każdy wie, co to jest linia!”Oni się mylą. Nie sądzę, żeby matematycy wiedzieli, czym są linie. A ponieważ ich teorie są zbudowane na ich metafizycznych twierdzeniach o „liniach i punktach”, teorie te muszą zostać zrewidowane od podstaw.
bez długości, szerokości i sensu
ponieważ pi jest tematem tego artykułu, przedstawmy definicję, której wszyscy nauczyliśmy się w szkole:
Pi jest stosunkiem obwodu okręgu do jego średnicy.
mamy tu kilka kluczowych terminów: „stosunek”, „okrąg”, „Obwód” i „średnica”.
aby zrozumieć, czym jest pi, musimy zrozumieć, co oznaczają te inne terminy. Szczególnie ten: „koło.”Oto jedna definicja:
” okrąg ” jest kształtem, którego granica składa się z punktów w równej odległości od ustalonego punktu.
brzmi rozsądnie. Jeszcze kilka kluczowych terminów, które musimy zrozumieć:” kształt”,” granica „i” punkty.”Jeśli chcemy zrozumieć pi, musimy zrozumieć, czym są okręgi, a jeśli chcemy zrozumieć, czym są okręgi, musimy najpierw zrozumieć, czym są „punkty”.
to tutaj znajduję podstawowy błąd dręczący ortodoksyjną geometrię: definicję punktu, z którego zbudowane są wszystkie inne obiekty geometryczne. O co chodzi? Okazuje się, że istnieje wiele różnych definicji. Zaczniemy od oryginalnej definicji Euklidesa, która mi się podoba.
„punktem” jest to, co nie ma części.
do tej definicji wrócimy później. Oto kolejny:
„punkt” jest dokładną lokalizacją lub miejscem na płaszczyźnie.
nieźle. Często są one reprezentowane przez małe kropki:

jednak te intuicyjne definicje nie są właściwie wykonalne we współczesnej matematyce. „Punkty”, w ortodoksyjnej geometrii, nie są tak naprawdę” zdefiniowane ” per se. Należy je rozumieć pod względem ich właściwości. Istotną właściwością jest to:
punkty nie mają żadnej długości, powierzchni, objętości ani żadnego innego atrybutu wymiarowego. Są to obiekty „zerowymiarowe”.
jest to absolutnie fundamentalne dla współczesnych koncepcji geometrii. Punkty nie mogą mieć żadnej długości, szerokości ani głębokości. A jednak wszystkie kształty są podobno z nich zbudowane. Możecie zapytać: „chwila, jak kształty, które mają wymiary, mogą składać się z kilku punktów, które nie mają wymiarów?”
to bardzo dobre pytanie i jeśli będziesz nalegał na znalezienie logicznej odpowiedzi, skończysz tak jak ja: odrzucając bardzo dużą część ortodoksyjnej matematyki.
każda „linia”, dla matematyka, w rzeczywistości składa się z nieskończonej liczby punktów – jednak każdy punkt jest sam w sobie bez żadnego wymiaru. Linie, które mają długość, składają się z punktów, które nie mają długości. Jak to ma sens?
nie ma.
to tak, jakby zapytać: „ile zer musisz dodać, aby otrzymać 1?”Odpowiedź jest oczywista: nie można dodać do siebie kilku zer i otrzymać 1-nawet nieskończoną ilość zer. jeśli punkt ma wymiary zerowe, to nie ma znaczenia, ile razem złożysz. Nigdy nie skończysz z obiektem wymiarowym. Jest to logiczna konieczność.
mamy więc bardzo duży problem. Dosłowny fundament, na którym zbudowana jest cała teoretyczna struktura nowoczesnej geometrii – „punkt” – jest wątpliwy. Błędy na tym poziomie mogą być katastrofalne.
kształty bez kształtu
Jeśli są spójne, matematyk szybko zmusza się do zajęcia nieparzystych pozycji. Na przykład, musi dojść do wniosku: „nie widzimy kształtów!”Weźmy przykład tego, co nie-matematycy nazywają „linią”:

z pewnością nie może to być linia dla matematyka, ponieważ linie podobno mają tylko jeden wymiar długości. Obiekt ten ma zarówno długość, jak i szerokość-jest wydłużony w dwóch wymiarach. Jak zatem możemy nazwać ten kształt, jeśli nie „linią”? Nie wiem – musisz zapytać matematyka.
a co z obiektem dwuwymiarowym: okręgiem?

oczywiście nie może to być okrąg. Obiekt ten składa się z pikseli, a nie punktów, a każdy piksel jest rozszerzony w dwóch wymiarach. Dlatego obiekt ma szorstkie krawędzie i nie jest idealnie gładki. Chociaż laicy mogą nazwać to „okręgiem”, jest to tylko zwykłe przybliżenie koła matematycznego, czasami nazywane „okręgiem doskonałym.”
to samo można powiedzieć o tajemniczym „punkcie”:

obiekty te również nie mogą kwalifikować się jako „punkty”, ponieważ mają wymiary. W końcu ich widzimy. Obiekty matematyczne nie mogą być widziane; nie mogą być wizualizowane; nie mogą mieć żadnego rozszerzonego – ani „rzeczywistego” – kształtu. Jeśli obiekt ma kształt, jeśli zajmuje przestrzeń, to musi się składać z przestrzennie rozszerzonych obiektów, podobnych do pikseli komputerowych, a nie punktów matematycznych.
Uwaga: Nie mówię tylko o „przestrzeni fizycznej” czy „kształcie fizycznym”. Mówię o kształtach każdego rodzaju. To, co widzę w moim polu widzenia – plamy koloru-mają kształt, ale nie są obiektami fizycznymi. Oni sami nie zajmują przestrzeni fizycznej. Są to mentalne reprezentacje i składają się z rozszerzonych punktów pikseli świetlnych na moim mentalnym ekranie.
powstaje więc naturalne pytanie:
czy ktoś, kiedykolwiek, widział lub doświadczył tych matematycznych kształtów w jakikolwiek sposób? Czy ktoś napotkał chociaż jedną prawdziwą „linię” lub „okrąg”? Odpowiedź musi być dobitna „Nie.”Wszystkie” linie „i” okręgi”, których faktycznie doświadczamy, mają wymiary. Zbudowane są ze skończonej liczby punktów, które same mają wymiary. Obiekty, których doświadczamy, składają się z pikseli.
znaczenie tego punktu nie może być przeceniane.
oznacza to, że każdy „okrąg”, jaki kiedykolwiek widziałeś – lub jakikolwiek inżynier kiedykolwiek zapisał na papierze – ma racjonalny stosunek obwodu do średnicy. Każdy „okrąg”, który kiedykolwiek został napotkany, ma unikalne” pi”, które można wyrazić jako stosunek dwóch liczb całkowitych.
„Obwód”, dla każdego okręgu, którego możemy doświadczyć, może być rozumiany jako „zewnętrzna granica kształtu”, która sama składa się ze skończonej liczby pikseli. Jego „średnica” jest również prostą liczbą całkowitą-liczbą pikseli, które ją tworzą. Umieść jedną liczbę całkowitą jako licznik i jedną liczbę całkowitą jako mianownik, i masz wymierne pi.
w rzeczywistości te prawdy powinny być niekontrowersyjne, nawet dla matematyków:
każdy „okrąg”, z którym kiedykolwiek się spotkałeś, bez wyjątku, ma racjonalne, skończone pi.
żaden „krąg”, z którym się kiedykolwiek spotkałeś, bez wyjątku nie ma irracjonalnego pi.
oznacza to, że moje twierdzenia o „racjonalnym pi” są prawdziwe dla co najmniej 99,9999% wszystkich kształtów, które nazywamy „kółkami”. Oznacza to również, że pi jest unikalne dla danego okręgu. Nie powinno to jednak dziwić, gdy pomyśli się o naturze proporcji.
wyobraź sobie, że miałem powiedzieć: „jaki jest stosunek wysokości stołu do długości?”
naturalnie odpowiesz: „która tabela?”
to samo dotyczy okręgów. Nie ma „jednego prawdziwego stosunku o nazwie’ pi '”z tego samego powodu nie ma” jednego prawdziwego stosunku wysokości do długości stołu.”Każdy stół i okrąg jest skonstruowany przez skończoną liczbę jednostek, ułożonych na różne sposoby, dlatego ich proporcje będą się różnić.
zgodnie ze standardową geometrią, istnieje dosłownie tylko jeden „okrąg”, do którego moje twierdzenia się nie odnoszą: tak zwany „idealny okrąg”-obiekt tak tajemniczy, że żaden śmiertelnik nigdy go nie napotkał.
Boski kształt
to „idealne koło” nie ma żadnych wymiernych boków ani krawędzi. Jego granica składa się z nieskończonej liczby punktów zero-wymiarowych. Najbardziej oddalone punkty zajmują dokładnie zerową przestrzeń. Jego pi nie może być wyrażone przez żadne rozszerzenie dziesiętne – ani nigdy nie będziemy dokładnie wiedzieć, czym jest jego pi.
obiekt ten nie może być skonstruowany, zwizualizowany, ani nawet istnieć w naszym świecie. Nasz świat jest na to zbyt niedoskonały. Zamiast tego żyje w innym świecie, do którego nasz umysł może mieć dostęp.
idealny okrąg jest tak wielki, że wszystkie inne „okręgi” są jedynie jego przybliżeniem. Jest to jedyny prawdziwy krąg. Jeśli poprosisz o dowód jego istnienia, nie znajdziesz żadnego. Jednak matematycy zbudowali całą swoją teorię geometryczną w oparciu o jej istnienie.
przyznaję się do swojej herezji: nie wierzę w „krąg doskonały.”
dlatego nie wierzę w ” irracjonalne pi.”Nie potrzebuję też takiej koncepcji. Każdy kształt, jaki kiedykolwiek spotkałem-lub kiedykolwiek spotkam – ma krawędzie, które zajmują przestrzeń.
geometria bez kół doskonałych i bez irracjonalnego pi jest w pełni wystarczająca do wyjaśnienia wszystkich zjawisk, których doświadczam. Dlatego nie muszę zakładać dodatkowej istoty – zwłaszcza takiej o tak niezwykłych właściwościach.
innymi słowy: po prostu wierzę w jeden krąg mniej niż matematycy. To wszystko, co jest wymagane do stwierdzenia, że pi jest liczbą wymierną dla dowolnego okręgu.
tylko abstrakcja!
słyszałem, że niektórzy matematycy twierdzą, że obiekty geometryczne są jedynie abstrakcją i dlatego są zwolnione z poprzedniej krytyki. Ale między innymi powoduje to cofnięcie metafizyki abstrakcji. Jesteś abstrakcyjny z betonów. Nie konkret z abstrakcji.
pomyśl o tym. Z czego wynika abstrakcja, aby uzyskać pojęcie „koła doskonałego”?
to nie mogą być okręgi, które faktycznie widzimy, ponieważ każde z tych okręgów ma niedoskonałe krawędzie. Wszystkie konkretne doświadczenia, które mamy, są kształtami o niedoskonałych krawędziach, racjonalnym pi i składają się z punktów o wymiarze. Na podstawie tych doświadczeń matematyk mówi: „Cóż, myślę, że prawdziwy okrąg to taki bez krawędzi, z irracjonalnym pi, i składa się z zero-wymiarowych punktów!”
to nonsens i nie tak działa abstrakcja.
wyobraź sobie, że mówimy o domach i abstrakcyjnych koncepcjach domów.
każdy dom, z którym się spotkaliśmy ma ściany, podłogę i sufit. Matematyk chce powiedzieć, że jego koncepcja „domu doskonałego” to taki bez ścian, podłóg czy sufitu. I w rzeczywistości, zwykłe stare domy są tylko przybliżeniem jego idealnego domu. Oczywiście, to błąd.
możemy mieć całkowicie poprawną abstrakcyjną koncepcję domu, ale właściwości naszego „abstrakcyjnego domu” muszą obejmować właściwości betonowych domów, z których jesteśmy abstrakcyjni. Nasz ” dom psychiczny „musi zawierać konceptualne kategorie” posiadania ścian, podłóg i sufitu.”Wymiary tych właściwości są nieistotne, o ile istnieją.
abstrakcyjna koncepcja „domu bez ścian, podłóg i sufitu” nie może wyjaśnić żadnych zjawisk, których doświadczamy, ponieważ nie opisuje rzeczy, która mogłaby istnieć. Wyobraź sobie, że twój przyjaciel zabiera Cię na puste pole i mówi: „Oto Mój idealny dom! Nie ma ścian, podłóg ani sufitu!”Można by pomyśleć, że jest szalony-zwłaszcza jeśli dodał,” a wszystkie inne domy są tylko przybliżeniem tego!”
nie prawdziwe!
jedna z bardziej obciążających odpowiedzi matematyków brzmi tak: „ale obiekty matematyczne nie są prawdziwe! W ogóle nie istnieją!”We wszystkich moich badaniach mogę śmiało powiedzieć, że matematyka jest jedynym obszarem myślenia, w którym przyznanie się” obiekty, o których mówię, nie są prawdziwe i nie istnieją ” ma na celu obronę konkretnej teorii.
ten błąd jest połączeniem obiektów i ich odniesień. Na przykład pojęcie ” mój dom „ma odnosić się do” mojego domu na świecie.”Głupio byłoby powiedzieć” Mój dom nie zajmuje miejsca, ponieważ mój pomysł na mój dom nie zajmuje miejsca.”
podobnie pojęcie” punktu „ma odnosić się do” dokładnego położenia w przestrzeni geometrycznej.”Równie głupio byłoby powiedzieć, że punkty nie zajmują przestrzeni geometrycznej, ponieważ moje wyobrażenie o punkcie nie zajmuje przestrzeni geometrycznej.”
podstawową istotą geometrii jest przestrzeń – czy to fizyczna, czy umysłowa, czy pojęciowa, czy jakikolwiek inny rodzaj przestrzeni. Dlatego też obiekty geometrii same muszą zajmować przestrzeń. Nie ma czegoś takiego jak „dokładna lokalizacja w przestrzeni, która nie jest dokładną lokalizacją w przestrzeni.”
Alternatywna teoria
pozwólcie, że przedstawię alternatywne ramy geometryczne. To dopiero początek zupełnie nowej teorii matematyki, którą nazywam ” matematyką jednostkową.”Oto podstawy geometrii Jednostki Bazowej:
1) wszystkie struktury geometryczne składają się z jednostek bazowych. Jednostki te określane są jako ” punkty.”
2) każdy punkt jest rozciągnięty przestrzennie.
3) w dowolnych ramach pojęciowych rozszerzenie Jednostki Bazowej wynosi dokładnie 1. W tych ramach z definicji nie ma mniejszej jednostki odległości.
4) Wszystkie odległości i kształty mogą być wyrażone w kategoriach Jednostki Bazowej.
te fundamenty tworzą logicznie solidny fundament, na którym można budować geometrię.
Połącz punkty i możesz skomponować dowolny kształt, bez żadnych irracjonalnych liczb. Każdy obiekt oprócz jednostki bazowej jest obiektem złożonym, złożonym z dyskretnych punktów. Dlatego powiedziałem wcześniej, że podoba mi się pierwotna definicja „punktu” Euklidesa jako „tego, co nie ma części.”Jednostki bazowe nie mają części; są to części, które tworzą każdą inną całość.
zdaję sobie sprawę, że będzie wiele zastrzeżeń do tego sposobu myślenia o geometrii. Zastrzeżenia te zostaną szczegółowo omówione w przyszłych artykułach.
aby uzyskać intuicję na temat tego frameworka, możesz myśleć o „punktach” jako o „pikselach”, których wszyscy mamy doświadczenie. Wszystkie kształty i obiekty, które możesz napotkać w symulacji VR w wysokiej rozdzielczości, to w rzeczywistości kępy pikseli, choć mogą wydawać się” idealnie gładkie ” z naszej makroskopowej perspektywy.
kilka ładnych implikacji tej teorii:
To jest linia:

To jest okrąg:

i ma wyraźnie racjonalne pi:
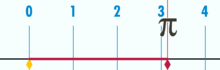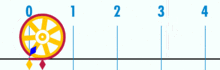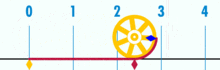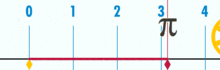
(uwaga: ten GIF został wzięty z Wikipedii, aby pokazać rzekomą irracjonalność pi. Jednak, jeśli jesteś świadomy tego, co oglądasz, jest to w rzeczywistości demonstracja racjonalności pi. Patrzysz na GIF logicznej perfekcji i precyzji geometrii Jednostki Bazowej!
Jaki jest stosunek obwodu tego koła do średnicy? Proste: jest to jedna liczba całkowita nad drugą-bez względu na to, ile jednostek podstawowych tworzy obwód, podzielonych przez to, ile jednostek tworzy średnicę. I tak się składa, że dopóki okrąg nie jest zbudowany z małej ilości jednostek bazowych, współczynniki pi będą się równać do około 3.14159 (chociaż, jeśli jesteśmy całkowicie precyzyjni, musimy mianować ułamkami, ponieważ Rozszerzanie dziesiętne może być wątpliwe w ramach jednostki bazowej. Ale to przyszły artykuł.). Nie ma „ogólnego” lub „idealnego” koła. Istnieją konkretne, rzeczywiste okręgi, z których każdy jest obiektem złożonym zbudowanym przez skończoną liczbę punktów.
między innymi oznacza to, że nie ma czegoś takiego jak” okrąg jednostkowy ” – domniemany okrąg o promieniu 1. Nie ma średnic, które mają odległość 1. Nie można utworzyć okręgu używając tylko jednego piksela.
w ramach tej teorii” kręgi ” są dokładnie tym, z czym się zetknąłeś. „Punkty „są lokalizacjami w przestrzeni, które są rzeczywistymi lokalizacjami w przestrzeni, a” linie ” są tym, o czym wszyscy wiedzą.
intuicja Jednostki Bazowej
oczywiście ten temat wymaga dużo więcej wyjaśnienia i pracy, nie tylko w geometrii, ale wszędzie tam, gdzie metafizyka matematyki jest błędna. Nie mogę opisać wszystkich zastrzeżeń do geometrii jednostki bazowej w tym artykule, ale wyjaśnię jeszcze kilka sposobów myślenia o tym i dlaczego jest ona lepsza od standardowej ortodoksji.
Po pierwsze, ta struktura w pełni wyjaśnia wszystkie zjawiska, których doświadczamy, i traci dokładnie zerową moc wyjaśniającą w porównaniu do Standardowej geometrii. Każdy kształt, każdy okrąg, każda linia, każdy punkt, każde doświadczenie przestrzenne, które kiedykolwiek będziemy mieli, może być wyjaśnione, bez zakładania istnienia dodatkowych Bytów. Nie doświadczamy doskonałych kręgów, dlatego nie mamy powodu do teoretyzowania na ich temat.
Co więcej, matematyka bazowo-jednostkowa jest bardziej logicznie dokładna niż ortodoksja. Każdy, kto pracował z „irracjonalnym pi” musi używać przybliżeń. Nie mogą używać rzeczywistego nieskończonego rozszerzenia dziesiętnego. Są zmuszeni arbitralnie odciąć wielkość pi, aby ją wykorzystać. Nie tak z geometrią Jednostki Bazowej. Doskonała precyzja jest rzeczywiście możliwa, ponieważ nie ma przybliżeń ani nieskończonych rozszerzeń dziesiętnych do czynienia. To może nie być nic wielkiego, ale w miarę zbliżania się technologii do wymiarów Jednostki Bazowej przestrzeni fizycznej, może to mieć duże znaczenie.
oto krótka, ciekawa strona o nieskończonym rozszerzaniu dziesiętnym pi:
Co się dzieje, gdy ortodoksyjni matematycy obliczają coraz więcej dziesiętnych Pi? Czy chwytają się „prawdziwych proporcji koła doskonałego”? Nie. To, co robią, to obliczanie współczynników pi dla okręgów o coraz mniejszych jednostkach bazowych. Gdy jednostka bazowa kurczy się – lub gdy okrąg staje się większy – stosunek jego obwodu do średnicy zmienia się coraz nieznacznie. Obliczenia te są natychmiast praktyczne, w taki sam sposób, w jaki tabele trygonometryczne są praktyczne. Są to wstępnie obliczone wartości, które są odpowiednie i dokładne dla danego okręgu o danej wielkości.
(Jeśli chcesz zrozumieć, dlaczego pi zmienia się nieznacznie, pomyśl o tym w ten sposób: wraz ze wzrostem wielkości jednostki podstawowej, obszar zamknięty obwodem kurczy się; gdy rozmiar jednostki podstawowej maleje, obszar zamknięty obwodem wzrasta, ale w tempie malejącym. Im gładsza krawędź okręgu, tym większy obszar okręgu.)
w tej notce: geometria jednostki bazowej nie wymaga „ostatecznej Jednostki Bazowej.”Innymi słowy, każdy schemat pojęciowy będzie miał jednostkę bazową przez logiczną konieczność, ale to nie znaczy, że nie możesz wymyślić innego schematu pojęciowego, który ma mniejszą jednostkę bazową.
pomyśl o tym w ten sposób: każde zdjęcie będzie zawierało skończoną liczbę pikseli. Będzie miał rozdzielczość Jednostki Bazowej. Nie oznacza to jednak, że niemożliwe jest zrobienie zdjęcia o wyższej rozdzielczości. podobnie, każdy okrąg będzie miał rozdzielczość jednostki bazowej, ale nie oznacza to, że niemożliwe jest wyobrażenie sobie takiego o wyższej rozdzielczości (mniejszych jednostek bazowych).
możemy nawet wpaść w granice świata fizycznego. Przestrzeń fizyczna musi mieć jednostkę bazową, co oznacza, że w naszym Układzie fizycznym nie ma mniejszej jednostki. Nie oznacza to jednak, że nie możemy mówić o mniejszych jednostkach bazowych. Te obiekty po prostu nie będą korelować z naszym wszechświatem. Kto wie-być może moglibyśmy powiedzieć prawdziwe rzeczy o innym fizycznym wszechświecie, który ma mniejsze jednostki bazowe.
uwaga: to również doskonale koreluje z moim postanowieniem do paradoksów Zenona. Przestrzeń musi mieć jednostkę bazową, jeśli ruch jest możliwy.
doskonałym przykładem zjawiska jednostki bazowej jest fraktal. Podobno fraktale mają sens tylko w ramach pojęciowych ” nieskończonej podzielności.”To nie jest poprawne. Fraktale mają większy sens w kontekście Jednostki Bazowej. Rozważ ten obrazek:

To wygląda jak główny kandydat do „nieskończonej podzielności.”Jest to jednak iluzja. W dowolnym momencie istnieje rozdzielczość jednostki bazowej dla tego obrazu. Gdy obraz „powiększa się”, tworzone są nowe jednostki, wszystkie wyrażone w pikselach. W żadnym momencie Nie patrzycie w nieskończoność; zawsze patrzycie na skończoną liczbę pikseli. Jeśli w to wątpisz, możesz policzyć piksele. Obiekt jest konstruowany podczas oglądania. To samo dzieje się w matematyce; obiekty są konstruowane w miarę ich wyobrażania. Wiele więcej zostanie powiedziane na ten temat w przyszłych artykułach.
wielokąty i Grecy
chcę szybko odnieść się do jednego sprzeciwu, który nieuchronnie się pojawi – tych, którzy twierdzą, że obrazy okręgów w tym artykule to nie są tak naprawdę okręgi, to są wielokąty. Krawędzie to kilka prostych linii; nie są idealnie gładkie. Jeśli to prawda, to nie jest to krytyka geometrii Jednostki Bazowej, ponieważ wszystkie okrągłe obiekty, które napotkamy, byłyby wielokątami. Dlatego nasze teorie matematyczne powinny dotyczyć wielokątów; niczego innego nie doświadczamy. Chcę wiedzieć o właściwościach tego kształtu:

I don ’ t care what you call it. Geometria jednostki bazowej może powiedzieć o właściwościach tego kształtu.
Grecy również popełnili ten błąd mówiąc o kręgach – jakby były zbudowane z „nieskończonej liczby linii.”Jest to nieprawidłowe. Okręgi i wielokąty składają się ze skończonej liczby punktów, a nie linii. Linie niczego nie komponują; same są obiektami złożonymi.
wyobraź sobie konstruowanie koła w piasku.

Jaki jest obszar tego okręgu? Gwarantuję, że to skończona, wymierna liczba. Można dosłownie policzyć ziarenka piasku, które go tworzą. Obwód składa się z ziaren piasku, podobnie jak średnica, podobnie jak Obszar. Wszystkie są liczbami całkowitymi.
ostatni argument, który poruszę w artykule, będzie pochodził od tych, którzy uważają, że „okrąg” nie jest kształtem, tylko wyrażeniem matematycznym. Coś w stylu (x2 + y2 = r2).
jest to po prostu kolejne metafizyczne zamieszanie, które łączy symbole z obiektem, który symbole mają opisywać. To tak, jakby powiedzieć: „’jabłka’ są synonimem słów ’ czerwony owoc.”To jest pomieszane. Słowa „czerwony owoc” są opisem przedmiotu, a nie samego przedmiotu. Wzór (x2 + y2 = r2) opisuje kształt okręgu – lub, jeśli wolisz myśleć o tym w ten sposób – jest to reguła konstruowania okręgu. To nie jest samo w sobie koło.
na tym zakończę ten artykuł. W przyszłości jest o wiele więcej do powiedzenia. Matematyka nie jest zwolniona z krytyki lub sceptycznych dociekań. Nie jest też zwolniona z potrzeby precyzyjnej metafizyki. Ze wszystkich powodów, które opisałem w tym poście, jest mnóstwo miejsca na alternatywne – i lepsze-koncepcje geometrii. Geometria jednostki bazowej nie traci mocy wyjaśniającej, eliminuje nieskończoną liczbę niepotrzebnych obiektów i daje logiczny fundament, na którym można zbudować mocniejszą teorię.
Jeśli Nie wierzysz w istnienie „okręgów doskonałych” – składających się z nieskończonej liczby zero-wymiarowych punktów – to nie wierzysz, że pi jest irracjonalne i dołączyłeś do niezwykle małej grupy intelektualnych trędowatych. Możecie teraz spodziewać się kpin i potępienia za Waszą herezję.
Jeśli podobał Ci się ten artykuł i chciałbyś wesprzeć tworzenie więcej herezji, odwiedź patreon.com/stevepatterson.