Trójkąt Skalenowy jest trójkątem o wszystkich bokach o różnych długościach.
wszystkie kąty są różne.
więc żadne boki nie są równe i żadne kąty nie są równe.
wzór na powierzchnię trójkąta skalarnego :
= √
gdzie
S = (a + b + c)/2
tutaj a, b i c są długościami bocznymi trójkąta.
problemy z ćwiczeniami
Problem 1:
znajdź obszar trójkąta skalenowego, którego długość boków wynosi 12 cm, 18 cm i 20 cm.
rozwiązanie:
ponieważ długości trzech boków są różne, trójkąt jest trójkątem skalenowym.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25 x 13 x 7 x 5)
= 5√455
zatem powierzchnia danego trójkąta skalarnego wynosi 5 √455 cm kwadratowych.
Problem 2:
boki trójkąta skalenowego mają 12 cm, 16 cm i 20 cm. Znajdź wysokość do najdłuższego boku.
rozwiązanie:
aby znaleźć wysokość do najdłuższego boku trójkąta, najpierw musimy znaleźć pole trójkąta.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
ponieważ chcemy znaleźć wysokość do najdłuższego boku, najdłuższy bok będzie podstawą trójkąta, jak pokazano poniżej.
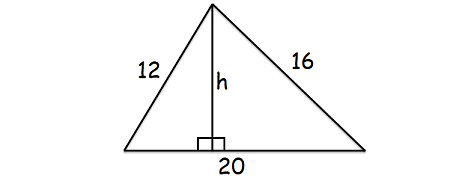
tutaj najdłuższy bok ma 20 cm.
Powierzchnia powyższego trójkąta = 96 cm2
(1/2) x 20 x h = 96
10h = 96
podziel każdą stronę przez 10.
h = 9.6 cm
więc wysokość do najdłuższego boku wynosi 9.6 cm.
Problem 3:
boki trójkąta skalenowego mają stosunek (1/2) : (1/3) : (1/4). Jeśli obwód wynosi 52 cm, a następnie znaleźć Długość najmniejszego boku.
rozwiązanie :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length najmniejszy bok ma 12 cm.
Problem 4:
powierzchnia trójkąta skalenowego wynosi 216 cm2, a boki są w stosunku 3 : 4 : 5. Znajdź obwód trójkąta.
rozwiązanie :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5X = 30
Obwód danego trójkąta skalarnego wynosi
= 18 + 24 + 30
= 72 cm
Problem 5:
jeden bok trójkąta skalarnego kąta prostego jest dwa razy drugi,a przeciwprostokątna wynosi 10 cm. Znajdź pole trójkąta.
rozwiązanie:
niech ” x ” będzie długością jednej z nóg trójkąta.
wtedy długość drugiej nogi wynosi 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2) (x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

oprócz rzeczy podanych powyżej, jeśli potrzebujesz innych rzeczy z matematyki, skorzystaj z naszej niestandardowej wyszukiwarki google tutaj.
jeśli masz jakieś uwagi na temat naszych treści matematycznych, napisz do nas:
zawsze doceniamy Twoją opinię.
możesz również odwiedzić następujące strony internetowe o różnych rzeczach z matematyki.
problemy ze słowem
problemy ze słowem HCF i LCM
problemy ze słowem na prostych równaniach
problemy ze słowem na równaniach liniowych
problemy ze słowem na równaniach kwadratowych
problemy ze słowem na algebrze
problemy ze słowem na pociągach
problemy ze słowem na obszarze i obwodzie
problemy słowne dotyczące bezpośredniej zmienności i odwrotnej zmienności
problemy słowne dotyczące ceny jednostkowej
problemy słowne dotyczące stawki jednostkowej
problemy słowne dotyczące porównywania stawek
konwersja zwyczajowych jednostek problemy słowne
Konwersja jednostek metrycznych word problemy
problemy słowne dotyczące odsetek prostych
problemy słowne dotyczące odsetek złożonych
problemy słowne dotyczące rodzajów kątów
Kąty uzupełniające i uzupełniające problemy słowne
Podwójne fakty problemy słowne
Trygonometria problemy słowne
procentowe problemy słowne
problemy z zyskiem i stratą
znaczniki i Markdown problemy ze słowem
problemy ze słowem dziesiętnym
problemy ze słowem na ułamkach
problemy ze słowem na mieszanych fraktrionach
jednoetapowe problemy ze słowem
nierówności liniowe problemy ze słowem
stosunek i proporcja problemów ze słowem
Czas i praca problemy ze słowem
problemy ze słowem na zestawach i diagramach Venna
problemy ze słowem na wieki
twierdzenie Pitagorasa problemy ze słowem
procent liczby problemy ze słowem na stałą prędkość
problemy ze słowem na średnią prędkość
problemy ze słowem na sumę kątów trójkąta wynosi 180 stopni
inne tematy
skróty zysków i strat
skróty procentowe
skróty tabeli czasów
skróty czasu, prędkości i dystansu
skróty proporcji i proporcji
Domena i zakres funkcji racjonalnych
dziedzina i zakres funkcji racjonalnych z dziurami
wykresy funkcji racjonalnych
wykresy funkcji racjonalnych z dziurami
Konwersja powtarzających się dziesiętnych na ułamki
Reprezentacja dziesiętna liczb racjonalnych
znajdowanie pierwiastka kwadratowego za pomocą długiego podziału
L. C.M metoda rozwiązywania problemów z czasem i pracą
tłumaczenie problemów słownych na Wyrażenia algebraiczne
reszta, gdy 2 potęga 256 jest podzielona przez 17
reszta, gdy 17 potęga 23 jest podzielona przez 16
suma wszystkich trzycyfrowych liczb podzielnych przez 6
suma wszystkich trzycyfrowych liczb podzielnych przez 7
suma wszystkich trzycyfrowe liczby podzielne przez 8
suma wszystkich trzech cyfr utworzonych za pomocą 1, 3, 4
suma wszystkich trzech czterocyfrowych liczb utworzonych za pomocą cyfr niezerowych
suma wszystkich trzech czterocyfrowych liczb utworzonych za pomocą 0, 1, 2, 3
suma wszystkich trzech czterocyfrowych liczb utworzonych za pomocą 1, 2, 5, 6