Rozkład normalny :definicja, problemy ze słowem

prawdopodobieństwo i Statystyka> rozkład normalny

zawartość:

1. co to jest rozkład normalny?
2. standardowy model normalny
3. problemy ze słowem rozkładu normalnego.
4. rozkład normalny na przykładach TI 89
5. Artykuły pokrewne.

co to jest rozkład normalny?

rozkład normalny.

rozkład normalny, czasami nazywany krzywą dzwonkową, jest rozkładem, który występuje naturalnie w wielu sytuacjach. Na przykład krzywa dzwonkowa jest widoczna w testach takich jak SAT i GRE. Większość studentów zdobędzie średnią (C), podczas gdy mniejsza liczba studentów zdobędzie B lub D. jeszcze mniejszy odsetek studentów zdobędzie F lub A. tworzy to rozkład, który przypomina dzwonek (stąd przydomek). Krzywa dzwonkowa jest symetryczna. Połowa danych spadnie na lewo od średniej; połowa spadnie na prawo.
wiele grup stosuje ten Typ wzorca. Dlatego jest szeroko stosowany w biznesie, statystyce i w organach rządowych, takich jak FDA:

• .
• błędy pomiaru.
• ciśnienie krwi.
• punkty na teście.
• wyniki IQ.
• pensje.

reguła empiryczna mówi ci, jaki procent Twoich danych mieści się w określonej liczbie odchyleń standardowych od średniej:
• 68% danych mieści się w jednym odchyleniu standardowym od średniej.
* 95% danych mieści się w dwóch standardowych odchyleniach średniej.
* 99,7% danych mieści się w trzech odchyleniach standardowych od średniej.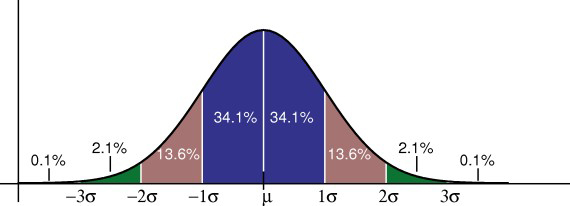

odchylenie standardowe kontroluje rozrzut rozkładu. Mniejsze odchylenie standardowe wskazuje, że dane są ściśle zgrupowane wokół średniej; rozkład normalny będzie wyższy. Większe odchylenie standardowe wskazuje, że dane są rozłożone wokół średniej; rozkład normalny będzie bardziej płaski i szerszy.

właściwości rozkładu normalnego

• średnia, tryb i mediana są równe.
• krzywa jest symetryczna w centrum (tzn. wokół średniej, μ).
• dokładnie połowa wartości znajduje się na lewo od środka i dokładnie połowa wartości jest na prawo.
• całkowita powierzchnia pod krzywą wynosi 1.

standardowy Model normalny
standardowy model normalny to rozkład normalny ze średnią 0 i odchyleniem standardowym 1.

standardowy model normalny: Dystrybucja danych

jednym ze sposobów ustalenia sposobu dystrybucji danych jest wykreślenie ich na wykresie. Jeśli dane są równomiernie rozłożone, możesz wymyślić krzywą dzwonową. Krzywa dzwonkowa ma niewielki procent punktów na obu ogonach i większy procent na wewnętrznej części krzywej. W standardowym modelu normalnym około 5 procent Twoich danych spadnie do” ogonów ” (w Kolorze ciemniejszym pomarańczowym na obrazku poniżej), a 90 procent będzie pomiędzy nimi. Na przykład, dla wyników testów uczniów rozkład normalny pokazywałby, że 2,5% uczniów uzyskało bardzo niskie wyniki, a 2.5 procent otrzymuje bardzo wysokie wyniki. Reszta będzie w środku; nie za wysoko lub za nisko. Kształt standardowego rozkładu normalnego wygląda następująco:

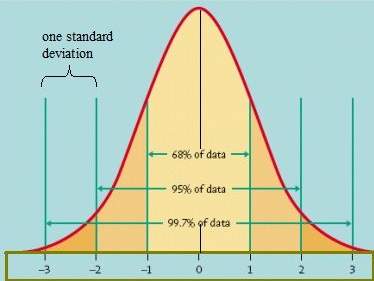
standardowy model normalny. Zdjęcie kredyt: University of Virginia.

praktyczne zastosowania standardowego modelu normalnego

standardowy rozkład normalny może pomóc w ustaleniu, w którym przedmiocie otrzymujesz dobre oceny, a w które przedmioty musisz włożyć więcej wysiłku ze względu na niskie procenty punktacji. Gdy otrzymasz wynik w jednym przedmiocie, który jest wyższy niż twój wynik w innym przedmiocie, możesz pomyśleć, że jesteś lepszy w temacie, w którym uzyskałeś wyższy wynik. Nie zawsze tak jest.

możesz tylko powiedzieć, że jesteś lepszy w danym temacie, jeśli uzyskasz wynik z pewną liczbą odchyleń standardowych powyżej średniej. Odchylenie standardowe mówi ci, jak mocno Twoje dane są zgrupowane wokół średniej; pozwala na porównanie różnych rozkładów, które mają różne typy danych-w tym różne środki.

na przykład, jeśli uzyskasz wynik 90 w matematyce i 95 w języku angielskim, możesz pomyśleć, że jesteś lepszy w języku angielskim niż w matematyce. Jednak w matematyce, Twój wynik jest 2 odchylenia standardowe Powyżej średniej. W języku angielskim jest to tylko jedno odchylenie standardowe Powyżej średniej. Mówi ci, że w matematyce Twój wynik jest znacznie wyższy niż większość uczniów (Twój wynik spada do ogona).
opierając się na tych danych, faktycznie wypadłeś lepiej z matematyki niż z angielskiego!

pytania dotyczące prawdopodobieństwa przy użyciu Modelu Standardowego

pytania dotyczące prawdopodobieństwa standardowego rozkładu normalnego mogą wydawać się niepokojące, ale kluczem do ich rozwiązania jest zrozumienie, co oznacza pole pod standardową krzywą normalną. Całkowita powierzchnia pod krzywą rozkładu normalnego wynosi 100% (to jest ” 1 ” jako dziesiętne). Na przykład, lewa połowa krzywej wynosi 50%, lub .5. Prawdopodobieństwo pojawienia się zmiennej losowej w lewej połowie krzywej wynosi .5.

oczywiście nie wszystkie problemy są takie proste, dlatego jest tabela Z. Wszystko, co robi tabela z, to mierzenie tych prawdopodobieństw (tj. 50%) i umieszczanie ich w standardowych odchyleniach od średniej. Średnia jest w centrum standardowego rozkładu normalnego, a prawdopodobieństwo 50% równa się Zero odchyleń standardowych.

standardowy rozkład normalny: jak znaleźć Prawdopodobieństwo (kroki)

Krok 1: narysuj krzywą dzwonka i cień w obszarze, o który jest pytany w pytaniu. Poniższy przykład pokazuje z > -0.8. Oznacza to, że szukasz prawdopodobieństwa, że z jest większe niż -0,8, więc musisz narysować pionową linię przy -0.8 odchyleń standardowych od średniej i odcień wszystkiego, co jest większe od tej liczby.

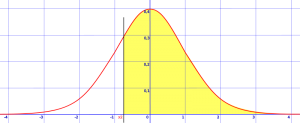
zacieniony obszar to z> -0.8

Krok 2: Odwiedź indeks obszaru normalnego prawdopodobieństwa i znajdź obraz, który wygląda jak Twój wykres. Postępuj zgodnie z instrukcjami na tej stronie, aby znaleźć wartość z dla wykresu. Wartość z jest prawdopodobieństwem.

Wskazówka: Krok 1 jest technicznie opcjonalny, ale zawsze dobrym pomysłem jest szkicowanie wykresu, gdy próbujesz odpowiedzieć na problemy ze słowem prawdopodobieństwa. To dlatego, że większość błędów zdarza się nie dlatego, że nie można wykonać matematykę lub odczytać z-tabeli, ale dlatego, że odejmujesz wynik z zamiast dodawać (tzn. wyobrażasz sobie prawdopodobieństwo pod krzywą w złym kierunku. Szkic pomaga w cementowaniu w głowie dokładnie tego, czego szukasz.

Jeśli nadal masz problemy, sprawdź korepetycje na Chegg.com. Twoje pierwsze 30 minut z nauczycielem na żywo jest bezpłatne!

problemy ze słowem o dystrybucji normalnej

ten film pokazuje przykład problemu ze słowem o dystrybucji normalnej. Więcej przykładów można znaleźć poniżej:

kiedy zajmujesz się rozkładem normalnym w klasie statystycznej, próbujesz znaleźć pole pod krzywą. Całkowita powierzchnia wynosi 100% (w układzie dziesiętnym jest to 1). Problemy rozkładu normalnego występują w sześciu podstawowych typach. Skąd wiesz, że problem ze słowem wiąże się z rozkładem normalnym? Poszukaj frazy kluczowej „Załóżmy, że zmienna jest normalnie rozproszona” lub ” Załóżmy, że zmienna jest w przybliżeniu normalna.”Aby rozwiązać problem ze słowem, musisz dowiedzieć się, jaki masz typ.

1. „między”: Zawierać frazę „between” i obejmuje górną i dolną granicę (tj. „Znajdź liczbę domów w cenie od 50 do 200 tysięcy”).
2. ” więcej niż „lub” powyżej”: Zawiera wyrażenie” więcej niż „lub”powyżej”.
3. „mniej niż”.
4. przykład Dolnego odcięcia (wideo)
5. przykład Górnego odcięcia (wideo)
6. przykład środkowego procentu (wideo)

„między”

Ten poradnik obejmuje rozwiązywanie problemów, które zawierają wyrażenie „między” i obejmuje górną i dolną granicę (np. „Znajdź liczbę domów w cenie od 50 000 $do 200 000$”. Zauważ, że różni się to od znalezienia „środkowego procentu” czegoś.

problemy ze słowem o normalnym rozkładzie: „Between”: kroki

Krok 1: Zidentyfikuj części problemu ze słowem. Słowo problem będzie identyfikować:

1. średnia (średnia lub μ).
2. odchylenie standardowe (σ).
3. wybrana liczba (np. „wybierz jedną losowo” lub „wybierz dziesięć losowo”).
4. X: liczby powiązane z „between” (tj. „between $5,000 and $10,000” będą miały X jako 5,000 i jako $10,000).

dodatkowo otrzymasz:

1. wielkość próby (tj. 400 domów, 33 osoby, 99 fabryk, 378 hydraulików itp.). Lub
2. możesz zostać poproszony o Prawdopodobieństwo (w takim przypadku rozmiar próbki będzie najprawdopodobniej każdy, np. „Journeyman Hydraulics” lub ” first year pilots.”

Krok 2: narysuj wykres. Umieść średnią zidentyfikowaną w Kroku 1 na środku. Umieść na wykresie liczbę związaną z „between” (Zgadnij, gdzie spadną liczby–nie musi być dokładna). Na przykład, jeśli twoja średnia wynosiła $100 i zostałeś poproszony o „wynagrodzenie godzinowe między $75 A $125”) Twój wykres będzie wyglądał mniej więcej tak:

Krok 3: Oblicz wyniki z. Podłącz pierwszą wartość X (na moim wykresie powyżej jest to 75) do Formuły wartości z i rozwiąż. Μ (średnia), jest 100 z wykresu próbki. Możesz uzyskać te liczby (w tym σ, odchylenie standardowe) z odpowiedzi w kroku 1 :

*Uwaga: Jeśli formuła Cię myli, cała ta formuła prosi Cię o to:
1. odejmij średnią od X
2. podziel przez odchylenie standardowe.

Krok 4: Powtórz krok 3 dla drugiego X.

Krok 5: weź liczby z kroku 3 i 4 i użyj ich, aby znaleźć obszar w tabeli Z.

Jeśli poproszono Cię o znalezienie prawdopodobieństwa w twoim pytaniu, przejdź do kroku 6a. jeśli poproszono Cię o znalezienie liczby z określonej wielkości próbki, przejdź do kroku 6B.

krok 6a:

Przelicz odpowiedź z kroku 5 na procent.

na przykład 0,1293 to 12,93%.

to jest to–pomiń krok 6b!

krok 6b

pomnóż Rozmiar próbki (znaleziony w kroku 1) przez wartość z znalezioną w kroku 4. Na przykład 0,300 * 100 = 30.

To jest to!

„więcej niż” lub „powyżej”

to how-to obejmuje rozwiązywanie problemów rozkładu normalnego, które zawierają wyrażenie „więcej niż” (lub wyrażenie takie jak „powyżej”).

Krok 1: Podziel problem ze słowem na części. Znajdź:

1. średnia (średnia lub μ)
2. odchylenie standardowe (σ)
3. Liczba (na przykład „wybierz pięćdziesiąt losowo” lub „wybierz 90 losowo”)
4. X: liczba związana z wyrażeniem „mniej niż”. Na przykład, jeśli poproszono Cię o znalezienie „pod $ 9,999”, to X wynosi 9,999.

Krok 2: Znajdź próbkę z problemu. Będziesz mieć albo określony rozmiar (jak „1000 telewizorów”) lub ogólną próbkę („każdy telewizor”).

narysuj obrazek, jeśli problem ze średnią i obszarem, którego szukasz. Na przykład, jeśli średnia wynosi $15 i poproszono Cię o sprawdzenie, jakie kolacje kosztują więcej niż $10, twój wykres może wyglądać następująco:

Krok 3: Oblicz wynik z (podłącz wartości do wzór wartości z i rozwiąż). Użyj odpowiedzi z kroku 1 :

zasadniczo wszystko, co robisz ze wzorem, to odjęcie średniej od X, a następnie podzielenie tej odpowiedzi przez odchylenie standardowe.

Krok 4: znajdź obszar za pomocą Z-score z kroku 3. Użyj tabeli Z. Nie wiesz, jak odczytać tabelę z? Zobacz film na stronie z-table.

Krok 6: Przejdź do kroku 6a, aby znaleźć Prawdopodobieństwo lub przejdź do kroku 6B, aby obliczyć określoną liczbę lub KWOTĘ.

krok 6a
Zmień odpowiedź kroku 5 na procent.

na przykład 0,1293 to 12,93%.

pomiń krok 6b: gotowe!

krok 6b
pomnóż wielkość próby z kroku 1 przez wynik z Z kroku 4. Na przykład 0,500 * 100 = 50.

gotowe!

mniej niż

to how-to obejmuje rozwiązywanie problemów ze słowem o rozkładach normalnych, które mają frazę „mniej niż” (lub podobną frazę, taką jak „mniej niż”).

problemy ze słowem o rozkładzie normalnym mniejsze niż: kroki

Krok 1: Podziel problem ze słowem na części:

1. średnia (średnia lub μ)
2. odchylenie standardowe (σ)
3. wybrana liczba (tj. „wybierz jeden losowo” lub „wybierz dziesięć losowo”)
4. X: liczba, która pasuje do „mniej niż” (tj. „pod $99,000” wyświetli X jako 99,000)

Plus, będziesz mieć albo:

1. określony rozmiar próbki. Na przykład 500 łodzi, 250 kanapek, 100 telewizorów itp.
2. wszyscy w próbce (zostaniesz poproszony o znalezienie prawdopodobieństwa). Na przykład „studenci pierwszego roku medycyny”, „pacjenci z chorobą nowotworową” lub ” piloci linii lotniczych.”

Krok 2: narysuj zdjęcie, które pomoże Ci zwizualizować problem. Poniższy wykres pokazuje średnią 15 i pole „poniżej 4”):

Krok 3: Znajdź wartość z, podłączając podane wartości do Formuły. „X” w naszym wykresie próbki wynosi 4, A μ (lub średnia) wynosi 15. Możesz uzyskać te liczby (w tym σ, odchylenie standardowe) z odpowiedzi w kroku 1, Gdzie zidentyfikowałeś części problemu:

wszystko, co musisz zrobić, aby rozwiązać formułę, to:

1. odjąć średnią od X.
2. podzielić przez odchylenie standardowe.

Krok 4: Weź liczbę z kroku 3, a następnie użyj tabeli z, aby znaleźć obszar.

Krok 5: aby znaleźć Prawdopodobieństwo, przejdź do kroku 6A. aby znaleźć liczbę z określonego podanego rozmiaru próbki, przejdź do kroku 6B.

krok 6a

Zmień liczbę z kroku 5 na procent.

na przykład 0,1293 to 12,93%.

To jest to!

krok 6b

pomnóż Rozmiar próbki (znaleziony w kroku 1) przez wartość z znalezioną w kroku 4. Na przykład 0,300 * 100 = 30.

To jest to!

Lower Cut Off

czasami w przypadku problemu ze słowem o dystrybucji normalnej zostaniesz poproszony o znalezienie „dolnej granicy górnego procentu” czegoś (np. Niższy punkt odcięcia to punkt, w którym wyniki spadną poniżej tego punktu. Na przykład, możesz chcieć dowiedzieć się, gdzie punkt odcięcia jest dla 10% uczestników testu.

sprawdź nasz kanał na YouTube, aby uzyskać więcej sprawdzonych problemów.

rozkład normalny TI 89 przykłady

w elementarnych statystykach często pojawia się pytanie, które zadaje ci punkty odcięcia dla pewnego procentu rozkładu normalnego, jak górne 90% lub górne 10%. Podczas pracy z tego typu problemów ręcznie jest uciążliwe, TI-89 Kalkulator graficzny sprawia, że lekka praca znalezienie odcięte punkty dla górnej procent z odwrotnej normalnej funkcji. To, co tak naprawdę robisz, to szukanie punktów odcięcia dla określonego percentyla: na przykład, jeśli masz listę ocen i chcesz wiedzieć, jaki wynik jest w 99. percentylu, możesz użyć odwrotnej funkcji normalnej, aby znaleźć ten procentowy punkt odcięcia.

znalezienie odciętych punktów dla najwyższego procentu

przykładowy problem: studenci w pewnej szkole średniej 5 stóp 8 cali (68 cali) wysoki. Wysokości są normalnie rozłożone, ze standardowym odchyleniem 2,5 cala. Jaka jest wartość, która oddziela 1% wysokości od reszty populacji?

Krok 1: Naciśnij aplikacje i użyj klawiszy przewijania, aby wyróżnić statystyki/edytor listy.

Krok 2: Naciśnij klawisz F5 2 1 (spowoduje to przejście do odwrotnego normalnego ekranu).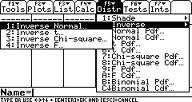

Krok 3: wprowadź 0.99 w polu obszaru.

Krok 4: Wpisz 68 w polu μ.

Krok 5: wprowadź 2.5 W polu σ.

Krok 6: naciśnij ENTER.

Krok 7: przeczytaj wyniki: odwrotność=73.8159 oznacza, że wysokość odcięcia dla 99.percentyla wynosi 73.8159 cali.

To jest to!

przykład proporcji prawdopodobieństwa (funkcja NormalCDF)

przykładowe pytanie: Grupa studentów z normalnie wypłaconymi pensjami zarabiają średnio 6800 USD z odchyleniem standardowym 2500 USD. Jaki odsetek studentów zarabia od 6500 do 7300 dolarów?

Krok 1: Naciśnij aplikacje. Przewiń do edytora statystyk / listy i naciśnij ENTER.

Krok 2: naciśnij F5 4.

Krok 3: wprowadź 6500 w polu niższa wartość.

Krok 4: wprowadź 7300 w górnym polu wartości.

Krok 5: wprowadź 6800 w polu μ.

Krok 6: wpisz 2500 w polu σ. Naciśnij ENTER.

Krok 7: przeczytaj odpowiedź. Cdf=.127018. Innymi słowy,.013, czyli 13% studentów zarabia od 6500 do 7300 dolarów.

TI-89 wykreślanie krzywej rozkładu normalnego

TI-89 może nie tylko obliczać z-scores i zwracać wartości dla rozkładów normalnych, ale może również wykreślić krzywą rozkładu normalnego. Wykres rozkładu normalnego może pomóc ci zobaczyć, czego powinieneś szukać, i daje Ci jeszcze jedno narzędzie do rozwiązywania problemów rozkładu normalnego. TI-89 może wykreślić krzywą rozkładu normalnego z obszarem zacienionym dla dowolnej wartości. Na przykład, można utworzyć wykres, który jest: mniej niż pewna liczba, więcej niż pewna liczba lub pomiędzy pewnym zbiorem liczb.

przykładowy problem: narysuj krzywą rozkładu normalnego dla wynagrodzeń studentów w typowym semestrze. Pensje studentów mają średnią 6800 dolarów i odchylenie standardowe 2500 dolarów. Zacienij obszar na wykresie, który odpowiada wynagrodzeniom między $7,300 a $9,000.

Krok 1: Naciśnij aplikacje i wybierz Edytor statystyk / listy.

Krok 2: naciśnij F2 3 i f2 4.

Krok 3: Naciśnij F5) 1.

Krok 4: przewiń w dół i wprowadź 7300 w polu niższa wartość.

Krok 5: przewiń w dół i wprowadź 9000 w górnym polu wartości.

Krok 6: przewiń w dół i wpisz 6800 w polu μ.

Krok 7: przewiń w dół i wprowadź 2500 w polu σ.

Krok 8: przewiń w dół. Obróć automatyczną skalę na „tak”, naciskając prawy klawisz przewijania, a następnie przycisk przewijania w dół, aby wybrać tak. Naciśnij ENTER.

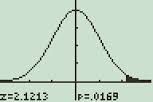
Wykres rozkładu normalnego wyświetlany na kalkulatorze TI-89.

To jest to!

końcówka: Jeśli chcesz wprowadzić ∞ (nieskończoność) jako jedną z dolnych lub górnych wartości, naciśnij klawisz diamentowy, a następnie Kataloguj.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, s. 533-534, 1987.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3 ed. Nowy Jork: Wiley, 1968.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” Krzywa błędów.”§6.4 w utworach matematycznych. 121-123, 1942.
Patel, J. K. I Read, C. B. Podręcznik rozkładu normalnego. Nowy Jork: Dekker, 1982.

1. jaka jest zasada 68-95-99.7?
2. transformacja Box Coxa
3. transformacja Box Mullera
4. modele mieszania Gaussa.
5. co to jest normalny Wykres prawdopodobieństwa?
6. Jak obliczyć wynik Z w statystykach
7. znajdź obszar po prawej stronie wyniku Z.
8. wykorzystanie aproksymacji normalnej do rozwiązania problemu dwumianowego
9. jaki jest współczynnik korekcji ciągłości?
10. pole pod indeksem krzywej rozkładu normalnego
11. centralne twierdzenie graniczne.
12. Rozkrzywiony rozkład normalny.
13. dwa ogony krzywej normalnej.
14. funkcja Q.

——————————————————————————

potrzebujesz pomocy w zadaniu domowym lub pytaniu testowym? Dzięki Chegg Study możesz uzyskać krok po kroku rozwiązania swoich pytań od eksperta w tej dziedzinie. Twoje pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!