techniki klasyfikacji są istotną częścią aplikacji uczenia maszynowego i eksploracji danych. Około 70% problemów w nauce o danych to problemy klasyfikacyjne. Istnieje wiele problemów klasyfikacyjnych, które są dostępne, ale regresja logistyczna jest powszechna i jest użyteczną metodą regresji do rozwiązania problemu klasyfikacji binarnej. Inną kategorią klasyfikacji jest klasyfikacja wielomianowa, która zajmuje się kwestiami, w których w zmiennej docelowej występuje wiele klas. Na przykład, IRIS dataset bardzo znany przykład klasyfikacji wielu klas. Inne przykłady to klasyfikowanie kategorii artykułów / blogów / dokumentów.
regresja logistyczna może być używana do różnych problemów klasyfikacyjnych, takich jak wykrywanie spamu. Przewidywanie, czy dany klient kupi konkretny produkt, czy też kupi innego konkurenta, czy użytkownik kliknie w dany link reklamowy, czy nie, a wiele innych przykładów jest w wiadrze.
regresja logistyczna jest jednym z najprostszych i najczęściej używanych algorytmów uczenia maszynowego do klasyfikacji dwuklasowej. Jest łatwy do wdrożenia i może być używany jako punkt odniesienia dla każdego problemu klasyfikacji binarnej. Jego podstawowe pojęcia fundamentalne są również konstruktywne w uczeniu głębokim. Regresja logistyczna opisuje i szacuje zależność między jedną zależną zmienną binarną a zmiennymi niezależnymi.
w tym samouczku nauczysz się następujących rzeczy w regresji logistycznej:
- Wprowadzenie do regresji logistycznej
- regresja liniowa Vs. regresja logistyczna
- maksymalne oszacowanie prawdopodobieństwa Vs. zwykła metoda najmniejszego kwadratu
- Jak działa regresja logistyczna?
- budowanie modeli w Scikit-ucz się
- oceny modeli za pomocą macierzy splątania.
- zalety i wady regresji logistycznej
regresja logistyczna
regresja logistyczna jest statystyczną metodą przewidywania klas binarnych. Zmienna wynik lub cel ma charakter dychotomiczny. Dychotomiczny oznacza, że istnieją tylko dwie możliwe klasy. Na przykład, może być stosowany do problemów z wykrywaniem raka. Oblicza prawdopodobieństwo wystąpienia zdarzenia.
jest to szczególny przypadek regresji liniowej, w którym zmienna docelowa ma charakter kategoryczny. Używa dziennika kursów jako zmiennej zależnej. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
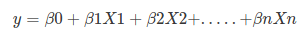
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
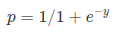
Apply Sigmoid function on linear regression:
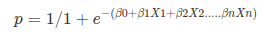
Properties of Logistic Regression:
- zmienna zależna w regresji logistycznej podąża za rozkładem Bernoulliego.
- Estymacja odbywa się poprzez maksymalne prawdopodobieństwo.
- nie ma kwadratu R, sprawność modelu jest obliczana poprzez Konkordancję, KS-Statystyka.
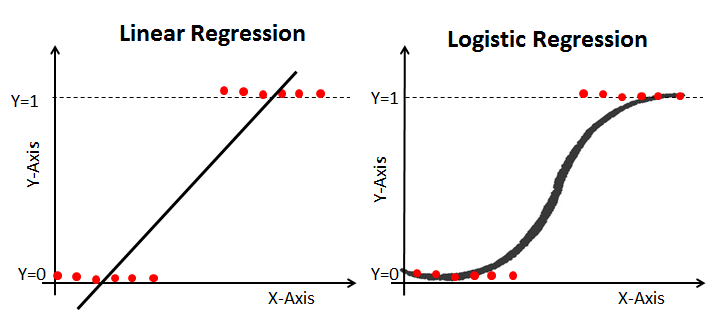
regresja liniowa Vs. regresja logistyczna
regresja liniowa daje ciągłą wydajność, ale regresja logistyczna zapewnia stałą wydajność. Przykładem ciągłej produkcji jest cena domu i cena akcji. Przykładem dyskretnego wyjścia jest przewidywanie, czy pacjent ma raka, czy nie, przewidywanie, czy klient odejdzie. Regresja liniowa jest szacowana przy użyciu zwykłych najmniejszych kwadratów (OLS), podczas gdy regresja logistyczna jest szacowana przy użyciu metody szacowania maksymalnego prawdopodobieństwa (mle).
maksimum prawdopodobieństwa Vs. metoda najmniejszego kwadratu
MLE jest metodą maksymalizacji „prawdopodobieństwa”, podczas gdy OLS jest metodą przybliżania minimalizującą odległość. Maksymalizacja funkcji prawdopodobieństwa określa parametry, które są najbardziej prawdopodobne do wytworzenia obserwowanych danych. Z statystycznego punktu widzenia MLE ustawia średnią i wariancję jako parametry przy określaniu konkretnych wartości parametrycznych dla danego modelu. Ten zestaw parametrów może być używany do przewidywania danych potrzebnych w rozkładzie normalnym.
zwykłe szacunki najmniejszych kwadratów są obliczane przez dopasowanie linii regresji na podanych punktach danych, która ma minimalną sumę odchyleń do kwadratu (błąd najmniejszego kwadratu). Oba są używane do oszacowania parametrów modelu regresji liniowej. MLE zakłada wspólną funkcję masy prawdopodobieństwa, podczas gdy OLS nie wymaga żadnych założeń stochastycznych do minimalizacji odległości.
funkcja esicy
funkcja esicy, zwana również funkcją logistyczną, daje krzywą w kształcie litery „S”, która może przyjąć dowolną liczbę rzeczywistą i odwzorować ją na wartość między 0 a 1. Jeśli krzywa idzie do dodatniej nieskończoności, y przewiduje się 1, a jeśli krzywa idzie do ujemnej nieskończoności, y przewiduje się 0. Jeśli wynik funkcji esicy jest większy niż 0,5, możemy sklasyfikować wynik jako 1 lub tak, a jeśli jest mniejszy niż 0.5, możemy sklasyfikować go jako 0 lub nie. Wynik nie pozwala na przykład: jeśli wynik wynosi 0,75, możemy powiedzieć w kategoriach prawdopodobieństwa jako: istnieje 75 procent szans, że pacjent będzie cierpiał na raka.
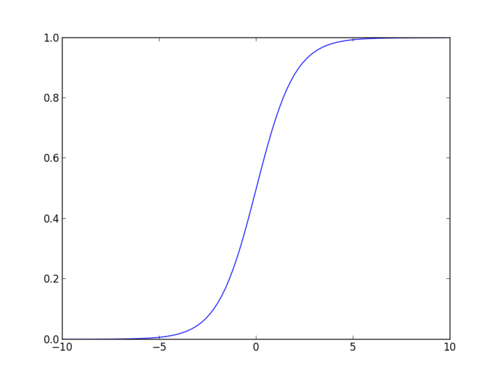
rodzaje regresji logistycznej
rodzaje regresji logistycznej:
- binarna regresja logistyczna: zmienna docelowa ma tylko dwa możliwe wyniki, takie jak spam lub nie spam, rak lub brak raka.
- regresja logistyczna wielomianowa: zmienna docelowa ma trzy lub więcej nominalnych kategorii, takich jak przewidywanie rodzaju wina.
- porządkowa regresja logistyczna: zmienna docelowa ma trzy lub więcej porządkowych kategorii, takich jak restauracja lub ocena produktu od 1 do 5.
budowanie modelu w Scikit-dowiedz się
zbudujmy model przewidywania cukrzycy.
tutaj masz zamiar przewidzieć cukrzycę za pomocą klasyfikatora regresji logistycznej.
najpierw załadujmy wymagany zestaw danych Pima Indian Diabetes za pomocą funkcji odczytu CSV pandy. Możesz pobrać dane z poniższego linku: https://www.kaggle.com/uciml/pima-indians-diabetes-database
Ładowanie Danych
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
wybór funkcji
tutaj należy podzielić podane kolumny na dwa typy zmiennych zależnych(lub zmiennych docelowych) i niezależnych(lub zmiennych funkcji).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variabledzielenie danych
aby zrozumieć wydajność modelu, podzielenie zestawu danych na zestaw treningowy i zestaw testowy jest dobrą strategią.
Podzielmy zbiór danych za pomocą funkcji train_test_split (). Musisz przekazać 3 Funkcje parametrów, cel i rozmiar test_set. Dodatkowo możesz użyć random_state do losowego wybierania rekordów.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)tutaj zbiór danych jest podzielony na dwie części w stosunku 75:25. Oznacza to, że 75% danych zostanie wykorzystane do szkolenia modeli, a 25% do testowania modeli.
opracowanie modelu i przewidywanie
najpierw zaimportuj moduł regresji logistycznej i utwórz obiekt klasyfikatora regresji logistycznej za pomocą funkcji LogisticRegression ().
następnie dopasuj swój model do zestawu pociągu za pomocą fit() i wykonaj predykcję na zestawie testowym za pomocą predict().
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)ocena modelu przy użyciu macierzy pomieszania
macierz pomieszania jest tabelą, która służy do oceny wydajności modelu klasyfikacyjnego. Można również wizualizować wydajność algorytmu. Podstawą macierzy pomieszania jest liczba poprawnych i niepoprawnych przewidywań sumowanych klasowo.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])tutaj można zobaczyć macierz zamieszania w postaci obiektu array. Wymiar tej macierzy wynosi 2*2, ponieważ ten model jest klasyfikacją binarną. Masz dwie klasy 0 i 1. Wartości diagonalne reprezentują dokładne przewidywania, podczas gdy elementy inne niż diagonalne są niedokładnymi przewidywaniami. W wyniku 119 i 36 są rzeczywistymi przewidywaniami, a 26 i 11 są błędnymi przewidywaniami.
Wizualizacja macierzy pomieszania za pomocą Heatmapy
wizualizujmy wyniki modelu w postaci macierzy pomieszania za pomocą matplotlib i seaborn.
tutaj wizualizujesz macierz zamieszania za pomocą Heatmapy.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
mierniki oceny macierzy błędów
ocenimy Model za pomocą mierników oceny modelu, takich jak dokładność, precyzja i przypomnienie.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226Cóż, masz wskaźnik klasyfikacji 80%, uważany za dobrą dokładność.
precyzja: precyzja polega na precyzji, czyli na tym, jak dokładny jest twój model. Innymi słowy, można powiedzieć, kiedy model przewiduje, jak często jest poprawny. W Twoim przypadku przewidywania, kiedy twój model regresji logistycznej przewiduje, że pacjenci będą cierpieć na cukrzycę, pacjenci mają 76% czasu.
Przypomnij: jeśli w zestawie testowym są pacjenci z cukrzycą, a model regresji logistycznej może ją zidentyfikować w 58% przypadków.
Krzywa ROC
charakterystyka działania odbiornika(ang. Receiver Operating characteristics, Roc) jest wykresem rzeczywistej wartości dodatniej względem wartości fałszywie dodatniej. Pokazuje kompromis między czułością a swoistością.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
wynik AUC dla przypadku wynosi 0,86. Wynik AUC 1 oznacza klasyfikator doskonały, a 0,5 oznacza klasyfikator bezwartościowy.
zalety
ze względu na swój wydajny i prosty charakter, nie wymaga dużej mocy obliczeniowej, łatwy do wdrożenia, łatwy do interpretacji, szeroko stosowany przez analityka danych i naukowca. Ponadto nie wymaga skalowania funkcji. Regresja logistyczna zapewnia wynik prawdopodobieństwa dla obserwacji.
wady
regresja logistyczna nie jest w stanie obsłużyć dużej liczby kategorycznych cech/zmiennych. Jest podatny na przepełnienie. Ponadto nie można rozwiązać problemu nieliniowego z regresją logistyczną, dlatego wymaga przekształcenia cech nieliniowych. Regresja logistyczna nie będzie dobrze działać z niezależnymi zmiennymi, które nie są skorelowane ze zmienną docelową i są bardzo podobne lub skorelowane ze sobą.
wnioski
w tym samouczku omówiłeś wiele szczegółów na temat regresji logistycznej. Nauczyłeś się, czym jest regresja logistyczna, jak budować odpowiednie modele, jak wizualizować wyniki i niektóre teoretyczne informacje podstawowe. Omówiłeś też kilka podstawowych pojęć, takich jak funkcja esicy, maksymalne prawdopodobieństwo, macierz splątania, krzywa ROC.
mamy nadzieję, że możesz teraz wykorzystać technikę regresji logistycznej do analizy własnych zbiorów danych. Dzięki za przeczytanie tego samouczka!
Jeśli chcesz dowiedzieć się więcej o regresji logistycznej, weź udział w kursie Datacamp Foundations of Predictive Analytics in Python (Part 1).