3.3 O Ciclo de Carnot | Maybaygiare.org

Seguinte: 3.4 Frigoríficos e Calor Até: 3. A primeira lei anterior: 3.2 A representação generalizada do Índice de conteúdos

um ciclo de Carnot é mostrada na figura 3.4. Tem quatro processos. Existem duas pernas adiabáticas reversíveis e duas pernas reversíveis. Podemos construir um ciclo Carnot com muitos sistemas diferentes, mas os conceitos podem ser mostrados usando um fluido de trabalho familiar, o gás ideal. O sistema pode ser considerado como uma câmara fechada por um pistão e cheia com este gás ideal.

Figura 3.4:ciclo de Carnot — termodinâmicos diagrama à esquerda e esquemática de thedifferent fases do ciclo para um sistema composto de um ideal gason o direito

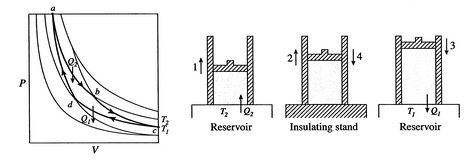
Os quatro processos no ciclo de Carnot são:

O sistema está na temperatura 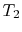estado . É trabalhada em contacto com um reservatório de calor, que é apenas um líquido ou uma massa sólida de uma extensão suficientemente grande para que a sua temperatura não mude de forma apreciável quando alguma quantidade de calor é transferida para o sistema. Em outras palavras, o reservatório de calor é uma constante temperaturesource (ou receptor) de calor. O sistema então passa por expansão anisotérmica de para , com calor absorvido .
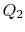Atstate, o sistema é termicamente isolado (removido do contato com o reservatório de calor) e, em seguida, deixe expandir para . Durante esta expansão, a temperatura diminui para . O calor trocado durante esta parte do ciclo, $$ Q_{bc} = 0.$ )
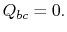no estado o sistema está em contacto com um reservatório de calor à temperatura . It isthen compressed to state 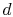, rejecting heat 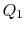in the process.finalmente, o sistema é comprimido adiabaticamente de volta ao estado inicial . The heat exchange $Q_{da} = 0$ .

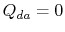A eficiência térmica do ciclo é dado pela definição

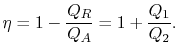$\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$

(3..4)

nesta equação, há uma convenção de sinais implícita. As quantidades como definidas são as magnitudes do calor absorvido e expulso. As quantidades por outro lado, são definedwith referência ao calor recebido pelo sistema. Neste exemplo, oformador é negativo e o último é positivo. O calor absorvido e expulso pelo sistema ocorre durante os processos isotérmicos e já sabemos quais são os seus valores de Eq.(3.1):

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 ,$

$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\quad \textrm {($Q_ 1$ é negativo.)}$

Theefficiency agora pode ser escrito em termos dos volumes thedifferent estados como

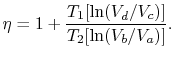$\displaystyle \eta = 1+ \frac{T_1}{T_2}.$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) mostrar duas consequências. Primeiro, os calores recebidos e rejeitados estão relacionadas as temperaturas da isotérmica partes do ciclo

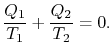$\displaystyle \frac{Q_1}{T_1}+\frac{Q_2}{T_2}= 0.$

(3..6)

em Segundo lugar, a eficiência de um ciclo de Carnot é dada de forma compacta por

$\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad\textbf{eficiência do ciclo de Carnot.}$

(3..7)

a eficiência só pode ser 100% se a temperatura a que o aquecimento é rejeitado for zero. As transferências de calor e de trabalho de e para o sistema são apresentadas esquematicamente no quadro 3.5.

figura 3.5:O trabalho e a transferência de calor ina ciclo de Carnot entre dois reservatórios de calor

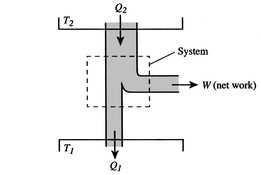
Enlameado Pontos

Desde $\eta = 1- {T_1}/{T_2}$ olhando para o gráfico, doesthat significa o mais distante isotérmicas são, thegreater eficiência? E que se eles fossem muito próximos, seria muito ineficiente? (MP 3.2)