Classificação de técnicas são uma parte essencial do aprendizado de máquina e mineração de dados de aplicativos. Aproximadamente 70% dos problemas na ciência dos dados são problemas de classificação. Existem muitos problemas de classificação que estão disponíveis, mas a regressão logística é comum e é um método de regressão útil para resolver o problema de classificação binária. Outra categoria de classificação é a classificação Multinomial, que lida com as questões em que várias classes estão presentes na variável alvo. Por exemplo, o conjunto de dados IRIS é um exemplo muito famoso de classificação multi-classe. Outros exemplos estão classificando a categoria Artigo/blog / documento.
regressão logística pode ser usada para vários problemas de classificação, tais como detecção de spam. Previsão de Diabetes, se um determinado cliente vai comprar um determinado produto ou vai churn outro concorrente, se o usuário vai clicar em um determinado link de propaganda ou não, e muitos mais exemplos estão no balde.
Regressão Logística é um dos algoritmos de aprendizagem de máquina mais simples e comumente usados para classificação de duas classes. É fácil de implementar e pode ser usado como base para qualquer problema de classificação binária. Seus conceitos fundamentais básicos também são construtivos na aprendizagem profunda. Regressão logística descreve e estima a relação entre uma variável binária dependente e variáveis independentes.
neste tutorial, você vai aprender o seguinte Regressão Logística:
- Introdução à Regressão Logística
- Regressão Linear Vs. Regressão logística
- Estimativa de Máxima Verossimilhança Vs. Ordinária Menos Quadrado Método
- Como fazer a Regressão Logística funciona?
- Model building in Scikit-learn
- Model Evaluation using Confusion Matrix.
- vantagens e desvantagens da regressão logística
Regressão Logística
regressão logística é um método estatístico para prever classes Binárias. A variável resultado ou alvo é de natureza dicotómica. Dicotômico significa que há apenas duas classes possíveis. Por exemplo, pode ser usado para problemas de detecção de câncer. Calcula a probabilidade de ocorrência de um evento.
é um caso especial de regressão linear em que a variável-alvo é categórica por natureza. Ele usa um log of odds como a variável dependente. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
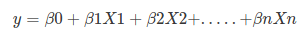
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
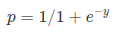
Apply Sigmoid function on linear regression:
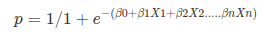
Properties of Logistic Regression:
- A variável dependente na regressão logística segue a distribuição de Bernoulli.a estimativa é feita através da máxima probabilidade.
- No R Square, Model fitness is calculated through Concordance, KS-Statistics.
regressão Linear Vs. Regressão Logística
regressão Linear dá-lhe uma saída contínua, mas a regressão logística proporciona uma saída constante. Um exemplo da produção contínua é o preço da casa e o preço das ações. Exemplo da saída discreta é prever se um paciente tem câncer ou não, prevendo se o cliente vai churn. A regressão Linear é estimada utilizando os mínimos quadrados ordinários (OLS), enquanto a regressão logística é estimada utilizando a abordagem da estimativa máxima da probabilidade (MLE).
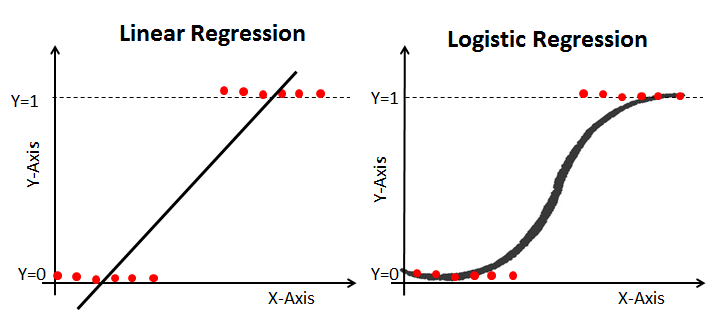
Estimativa de Máxima Verossimilhança Vs. Menos Quadrado Método
O MLE é uma “probabilidade” maximização do método OLS é uma distância de minimizar o método de aproximação. Maximizar a função de probabilidade determina os parâmetros que são mais propensos a produzir os dados observados. De um ponto de vista estatístico, MLE define a média e variância como parâmetros na determinação dos valores paramétricos específicos para um determinado modelo. Este conjunto de Parâmetros pode ser usado para prever os dados necessários em uma distribuição normal.as estimativas dos mínimos quadrados ordinários são calculadas ajustando uma linha de regressão em determinados pontos de dados com a soma mínima dos desvios ao quadrado (erro mínimo quadrado). Ambos são usados para estimar os parâmetros de um modelo de regressão linear. MLE assume uma função de massa de probabilidade conjunta, enquanto OLS não requer suposições estocásticas para minimizar a distância.
função Sigmoid
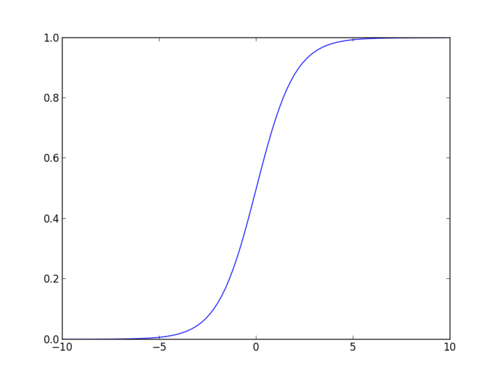
a função sigmoid, também chamada função logística dá uma curva em forma de ‘ S ‘ que pode tomar qualquer número real e mapeá-lo em um valor entre 0 e 1. Se a curva for para o infinito positivo, o y previsto tornar-se-á 1, e se a curva for para o infinito negativo, o y previsto tornar-se-á 0. Se a saída da função sigmoid for superior a 0.5, podemos classificar o resultado como 1 ou SIM, e se for inferior a 0.5, podemos classificá-lo como 0 ou não. O output não pode, por exemplo: se o output é 0,75, podemos dizer em termos de probabilidade como: há 75 por cento de chance de que o paciente vai sofrer de câncer.
Tipos de Regressão Logística
Tipos de Regressão Logística:
- Binário de Regressão Logística: variável-alvo tem apenas dois resultados possíveis, tais como Spam ou Não Spam, Câncer ou Não Câncer.Regressão Logística Multinomial: a variável alvo tem três ou mais categorias nominais, como a previsão do tipo de vinho.Regressão Logística Ordinal: a variável alvo tem três ou mais categorias ordinais, tais como a classificação de restaurante ou produto de 1 a 5.
Model building in Scikit-learn
Let’s build the diabetes prediction model.
Aqui, você vai prever a diabetes usando classificador de regressão logística.vamos primeiro carregar o conjunto de dados de Diabetes Indiano Pima necessário usando a função CSV de leitura dos pandas. Você pode fazer o download de dados a partir do seguinte link: https://www.kaggle.com/uciml/pima-indians-diabetes-database
o Carregamento de Dados
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
Selecionando o Recurso
Aqui, você precisa dividir o dado colunas em dois tipos de variáveis dependente(ou variável-alvo) e variável independente(ou recurso de variáveis).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variabledividindo dados
para compreender o desempenho do modelo, dividindo o conjunto de dados em um conjunto de treinamento e um conjunto de teste é uma boa estratégia.
vamos dividir o conjunto de dados usando a função train_test_split(). Você precisa passar 3 características de parâmetros, alvo, e tamanho test_ set. Além disso, você pode usar random_ State para selecionar registros aleatoriamente.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)Aqui, o conjunto de dados é dividido em duas partes, em uma proporção de 75:25. Isso significa que 75% dos dados serão usados para treinamento de modelos e 25% para testes de modelos.
desenvolvimento e previsão do Modelo
primeiro, importar o módulo de regressão logística e criar um objeto classificador de regressão logística usando a função de regressão logística ().
então, encaixe o seu modelo no conjunto do comboio usando fit () e realize a previsão no conjunto de teste usando predict().
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)Model Evaluation using Confusion Matrix
a confusion matrix is a table that is used to evaluate the performance of a classification model. Você também pode visualizar o desempenho de um algoritmo. O fundamental de uma matriz de confusão é o número de previsões corretas e incorretas são resumidas em termos de classe.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])Aqui, você pode ver a confusão matriz na forma do objeto array. A dimensão desta matriz é 2*2 porque este modelo é uma classificação binária. Tem duas classes 0 e 1. Os valores diagonais representam previsões precisas, enquanto os elementos não-diagonais são previsões imprecisas. Na saída, 119 e 36 são previsões reais, e 26 e 11 são previsões incorretas.
Visualizing Confusion Matrix using Heatmap
let’s visualize the results of the model in the form of a confusion matplotlib and seaborn.
Aqui, você irá visualizar a matriz de confusão usando o Heatmap.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
Confusão Matriz de Avaliação de Métricas
Vamos avaliar o modelo de avaliação do modelo de métricas como o rigor, a precisão e o recall.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226Well, you got a classification rate of 80%, considered as good accuracy.
Precisão: Precisão é sobre ser preciso, ou seja, quão preciso é o seu modelo. Em outras palavras, você pode dizer, quando um modelo faz uma predição, quantas vezes é correto. No seu caso de previsão, quando o seu modelo de regressão logística previu que os pacientes vão sofrer de diabetes, que os pacientes têm 76% do tempo.
Recall: se há pacientes com diabetes no conjunto de testes e seu modelo de regressão logística pode identificá-lo 58% do tempo.curva ROC
curva ROC
característica de funcionamento do receptor(ROC) é um gráfico da taxa verdadeira positiva contra a taxa falsa positiva. Mostra a troca entre sensibilidade e especificidade.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
AUC pontuação para o caso é de 0.86. A AUC score 1 representa um classificador perfeito, e 0, 5 representa um classificador sem valor.
vantagens
por causa de sua natureza eficiente e direta, não requer alto poder computacional, fácil de implementar, facilmente interpretável, usado amplamente pelo analista de dados e cientista. Além disso, não requer escala de recursos. Regressão logística fornece uma pontuação de probabilidade para observações.
desvantagens
regressão logística não é capaz de lidar com um grande número de características/variáveis categóricas. É vulnerável a sobreposições. Além disso, não pode resolver o problema não-linear com a regressão logística que é por isso que requer uma transformação de características não-lineares. A regressão logística não irá funcionar bem com variáveis independentes que não estão correlacionadas com a variável-alvo e são muito semelhantes ou correlacionadas umas com as outras.
conclusão
neste tutorial, você cobriu um monte de detalhes sobre Regressão Logística. Você aprendeu o que é a regressão logística, como construir os respectivos modelos, como visualizar os resultados e algumas das informações teóricas de fundo. Além disso, você cobriu alguns conceitos básicos, tais como a função sigmoid, máxima probabilidade, matriz de confusão, curva ROC.
esperançosamente, você pode agora utilizar a técnica de regressão logística para analisar seus próprios conjuntos de dados. Obrigado por ler este tutorial!
Se você gostaria de aprender mais sobre Regressão Logística, tome os fundamentos de DataCamp de análise preditiva em Python (Parte 1) curso.