especialização: intermédia
O que é uma função de linha?precisamos saber quais são as características essenciais das linhas antes de considerar como construir um sistema de base para elas.as funções de linha são formadas unindo polinômios em nós pontualmente fixos. Isto é, nós dividimos o intervalo que se estende do limite inferior tL toupper limit tU sobre o qual nós queremos aproximar uma curva em L+1 sub-intervalada por L limites interiores ξl chamados nós, ou às vezes breakpoints.Há uma distinção entre estes dois termos, mas vamos chegar a isso mais tarde.
considere o caso mais simples no qual um único ponto de ruptura divide o intervalo em duas sub-entradas. A fragmentação é, dentro de cada intervalo, um polinômio de grau especificado(a maior potência que define o polinômio) ou ordem (o número de coeficientes que definem o polinômio, que é um mais do que seu grau). Vamos usar m para designar a ordem do polinômio, de modo que o grau seja m – 1:
no ponto de ruptura interior ξ1, os dois polinômios são obrigados a se unir suavemente. No caso mais comum, isto significa que os derivados correspondem à ordem um a menos do que o grau. De fato, se eles correspondessem com o derivado cuja ordem igualava o grau, eles seriam o mesmo polinômio. Assim, uma função de linha definida neste ERA tem um grau extra de liberdade do que um polinômio estendendo-se ao longo de todo o intervalo.por exemplo, que cada polinômio seja um segmento de linha reta, e portanto de grau Um. Neste ponto, eles se unem no ponto de ruptura com Derivatives correspondentes até o grau 0; em suma, eles simplesmente se unem e têm valores idênticos no ponto de ruptura. Desde o primeiro polinômio tem dois graus de liberdade (inclinação e interseção), e o segundo, tendo o seu valor já definido no ponto de quebra,fica com apenas um grau de liberdade (declive), o total da linha poligonal tem threedegrees de liberdade.correspondentemente, se ambos os polinômios são quadráticos, então a correspondência tanto em termos de valores quanto em termos de slope do primeiro derivado ξ1. O primeiro polinômio tem três graus de liberdade, mas o segundo perde dois porque se a restrição em seu valor e declive em ξi, e assim retém apenas um. Isto deixa um total de quatro graus de liberdade para a fragmentação formada desta forma, opondo-se a três para um polinômio quadrático ao longo de todo o intervalo. A figura 1 mostra os casos lineares e quadráticos com um único ponto de paragem.
Quais são alguns exemplos de funções de base comumente usadas?
agora podemos generalizar a situação para L pontos de paragem interiores, e uma função spline sendo de ordem m ou grau m – 1 sobre o intervalo eachsub. O primeiro segmento polinomial tem um complemento completo de graus m de liberdade, mas cada segmento subsequente tem apenas uma árvore livre por causa das restrições m – 1 em seu comportamento.Isto dá um total de graus L + M de liberdade, ou número de pontos de paragem inferiores mais a ordem dos segmentos polinomiais.
Thus, spline functions are essentially generalizations of the notion of polygonallines. Eles ganham sua flexibilidade de duas maneiras: em primeiro lugar, pela Ordem dos polinômios a partir dos quais são construídos, e em segundo lugar, pelo número de pontos de ruptura utilizados. Nós geralmente optamos por manter a ordem fixa, e adicionar pontos de paragem como necessário para obter a flexibilidade necessária.
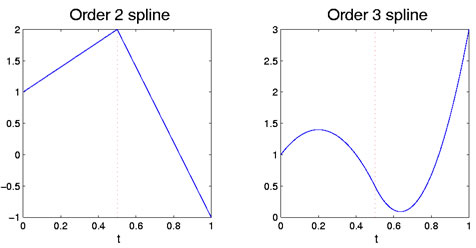
Figura 1: a figura esquerda mostra uma ordem de duas funções de linha, que é em trechos lineares. A figura direita é uma linha de ordem 3, que é quadratica em trechos. O ponto de ruptura a 0,5 é indicado pela linha vertical vermelha pontilhada.