Definição
Um polinômio na variável x é uma função que pode ser escrita na forma,
onde an, an-1 , … a2, a1, a0 são constantes. Nós chamamos o termo que contém a maior potência de x (i.e. anxn) o termo líder, e nós chamamos um coeficiente líder. O grau do polinômio é o poder de x no termo principal. Nós já vimos graus 0, 1 e 2 polinômios que eram as funções constantes, lineares e quadráticas, respectivamente. Grau 3, 4 e 5 polinômios também têm nomes especiais.: funções cúbicas, quarticas e quínticas. Polinômios com grau n > 5 são apenas chamados polinômios de grau nth. Os nomes de diferentes funções polinomiais são resumidos na tabela abaixo.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
o comportamento limitante dos polinômios
o comportamento limitante de uma função descreve o que acontece à função como x → ±∞. O grau de um polinômio e o sinal de seu coeficiente líder ditam seu comportamento limitante. Estes resultados estão resumidos na tabela seguinte.
Você pode usar esta informação para determinar se um polinômio tem ou não um grau Ímpar ou par e se o coeficiente líder é positivo ou negativo, simplesmente inspecionando seu grafo.
os seguintes grafos de polinômios exemplificam cada um dos comportamentos descritos na tabela acima.
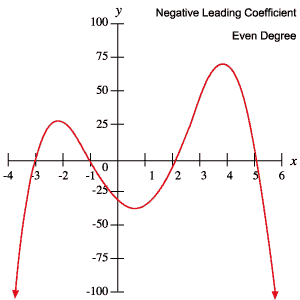
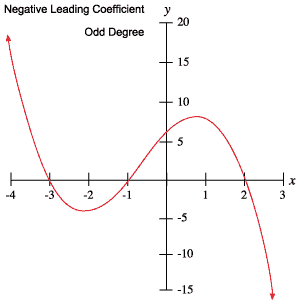
Raízes e Pontos de Viragem
O grau de um polinômio diz a você mesmo mais do que a limitação de comportamento. Especificamente, um polinômio de grau n pode ter no máximo n raízes reais (X-interceptações ou zeros) contando multiplicidades. Por exemplo, suponha que estamos olhando para um polinômio de 6º grau que tem 4 raízes distintas. Se duas das quatro raizes têm multiplicity 2 e os outros 2 têm multiplicity 1, nós sabemos que não há nenhuma outra raizes porque nós contabilizamos todas as 6 raizes. Isto é porque as raizes com uma multiplicidade de dois (também conhecidas como raizes duplas) são contadas como duas raizes.
estar ciente de que uma necessidade polinomial de grau n não tem raízes reais — pode ter menos porque tem raízes imaginárias. Observe que um polinômio de grau ímpar deve ter pelo menos uma raiz real, uma vez que a função se aproxima – ∞ em uma extremidade e + ∞ na outra; uma função contínua que muda de negativo para positivo deve Intersectar o eixo x algures no meio. In addition, an nth degree polynomial can have at most n – 1 turning points. Um ponto de viragem é um ponto em que a função muda de aumentar para diminuir ou diminuir para aumentar, como se vê na figura abaixo. Novamente, uma necessidade polinomial de nth grau não tem pontos de viragem n – 1, poderia ter menos.
Nota de Cautela
é importante perceber a diferença entre pares e ímpares e funções pares e ímpares grau de polinˆ omios. Qualquer função, f(x), ou mesmo se,
f(−x) = x,
para todo x no domínio de f(x), ou a estranho, se,
f(−x) = −x,
para todo x no domínio de f(x), ou nem mesmo nem estranho se nenhuma das alternativas acima são verdadeiras declarações.
um polinômio de grau kth, p (x), é dito ter um grau par Se k é um número par e um grau ímpar Se k é um número ímpar. Lembre-se que mesmo se p(x) tem grau par, não é necessariamente uma função par. Da mesma forma, se p(x) tem grau ímpar, não é necessariamente uma função ímpar.
também usamos os Termos par e ímpar para descrever raízes de polinômios. Especificamente, um p(x) polinomial tem raiz x = a de multiplicidade k (i.e. x = A é uma raiz repetida vezes k) se (x − A)k é um fator de p(x). Dizemos que x = A tem mesmo multiplicidade se k é um número par e uma multiplicidade ímpar Se k é um número ímpar.
domínio e gama
Todos os polinômios têm o mesmo domínio que consiste de todos os números reais. A gama de polinômios de grau ímpar também consiste de todos os números reais. A gama de polinômios de grau par é um pouco mais complicada e não podemos explicitamente declarar a gama de todos os polinômios de grau par. Se o coeficiente de liderança for positivo, a função se estenderá para+ ∞; enquanto que se o coeficiente de liderança for negativo, ele se estenderá para -∞. Isto significa que até mesmo polinômios de grau com coeficiente de liderança positivo têm alcance onde ymax denota o máximo global da função atinge. Em geral, não é possível determinar analiticamente os máximos ou mínimos dos polinômios.
** * *
na próxima seção você aprenderá a divisão polinomial, uma técnica usada para encontrar as raízes das funções polinomiais.
divisão polinomial