Distribuição Normal (Curva de gauss): Definição de Problemas do Word

Probabilidade e Estatística > distribuição Normal

Conteúdo:

1. o Que é uma distribuição Normal?
2. O modelo Normal Padrão
3. problemas de Palavras de distribuição normais.distribuição Normal nos exemplos artigos relacionados.o que é uma distribuição Normal?
   por favor, aceite estatísticas, cookies de marketing para ver este vídeo.
   

   uma distribuição normal.

   Uma distribuição normal, às vezes chamada de curva de sino, é uma distribuição que ocorre naturalmente em muitas situações. Por exemplo, a curva da campainha é vista em testes como o SAT e o GRE. A maior parte dos alunos vai marcar a média (C), enquanto um número menor de alunos vai marcar um B ou D. Uma porcentagem ainda menor de alunos marcar um F ou um A. isto cria uma distribuição que se assemelha a um sino (daí o apelido). A curva da campainha é simétrica. Metade dos dados cairá para a esquerda da média; metade cai para a direita.muitos grupos seguem este tipo de padrão. É por isso que é amplamente utilizado em negócios, estatísticas e em organismos governamentais como a FDA:

   • alturas das pessoas.erros de medição.tensão arterial.pontos num ensaio.pontuação de QI.salários.

   a regra empírica diz-lhe qual a percentagem dos seus dados se situa dentro de um certo número de desvios-padrão da média:
   • 68% dos dados se situa dentro de um desvio-padrão da média.95% dos dados estão dentro de dois desvios padrão da média.
   • 99,7% dos dados estão dentro de três desvios padrão da média.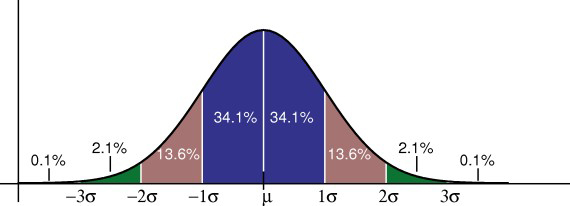
   

   O desvio padrão controla a propagação da distribuição. Um desvio padrão menor indica que os dados estão firmemente agrupados em torno da média; a distribuição normal será mais alta. Um desvio padrão maior indica que os dados são distribuídos em torno da média; a distribuição normal será mais plana e mais ampla.

   propriedades de uma distribuição normal

   • A média, modo e mediana são todos iguais.
   • a curva é simétrica no centro (isto é, em torno da média, μ).
   • exatamente metade dos valores estão à esquerda do centro e exatamente metade dos valores estão à direita.a área total sob a curva é 1.

   o modelo Normal Padrão
   Um modelo normal padrão é uma distribuição normal com uma média de 0 e um desvio padrão de 1.

   modelo Normal Padrão: Distribuição de dados

   uma maneira de descobrir como os dados são distribuídos é plotá-los em um gráfico. Se os dados forem distribuídos uniformemente, você pode vir acima com uma curva da campainha. Uma curva de sino tem uma pequena porcentagem dos pontos em ambas as caudas e a maior porcentagem na parte interna da curva. No modelo normal Padrão, Cerca de 5 por cento de seus dados cairiam nas “caudas” (cor de laranja escuro na imagem abaixo) e 90 por cento estarão no meio. Por exemplo, para resultados de testes de alunos, a distribuição normal mostraria 2,5 por cento dos alunos obtendo resultados muito baixos e 2.5% a obter resultados muito altos. O resto será no meio; não muito alto ou muito baixo. A forma da distribuição normal padrão se parece com esta:

   

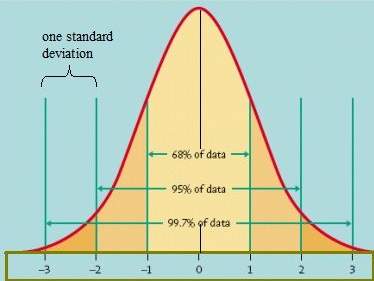
   o modelo Padrão normal. Image credit: University of Virginia.

   aplicações práticas do modelo Normal Padrão

   a distribuição normal padrão pode ajudá-lo a descobrir qual o assunto em que está a obter boas notas e quais os assuntos em que tem de exercer mais esforço devido às percentagens de pontuação baixas. Uma vez que você começa uma pontuação em um assunto que é maior do que sua pontuação em outro assunto, você pode pensar que você é melhor no assunto onde você conseguiu a pontuação mais elevada. Isso nem sempre é verdade.

   Você só pode dizer que você é melhor em um assunto particular se você obter uma pontuação com um certo número de desvios padrão acima da média. O desvio padrão diz-lhe como os seus dados estão apertados em torno da média; permite — lhe comparar diferentes distribuições que têm diferentes tipos de dados-incluindo diferentes meios.

   Por exemplo, se você tiver uma pontuação de 90 em Matemática e 95 em inglês, você pode pensar que você é melhor em Inglês do que em Matemática. No entanto, em Matemática, sua pontuação é 2 desvios padrão acima da média. Em inglês, é apenas um desvio padrão acima da média. Ele lhe diz que em Matemática, sua pontuação é muito maior do que a maioria dos alunos (sua pontuação cai na cauda).baseado nestes dados, você realmente teve melhor desempenho em Matemática do que em inglês!

   perguntas de probabilidade usando o modelo padrão

   perguntas sobre a distribuição normal padrão probabilidade pode parecer alarmante, mas a chave para resolvê-las é entender o que a área sob uma curva normal padrão representa. A área total sob uma curva de distribuição normal padrão é 100% (ou seja,” 1 ” como uma casa decimal). Por exemplo, a metade esquerda da curva é de 50%, ou .5. Então a probabilidade de uma variável aleatória aparecer na metade esquerda da curva é .5.

   claro, nem todos os problemas são tão simples, e é por isso que há uma tabela-Z. Tudo o que uma tabela z faz é medir essas probabilidades (ou seja, 50%) e colocá-las em desvios padrão em relação à média. A média está no centro da distribuição normal padrão, e uma probabilidade de 50% é igual a desvios padrão zero.

   distribuição normal Padrão: Como encontrar a probabilidade (passos)

   Passo 1: desenhar uma curva da campainha e sombrear na área que é pedida na pergunta. O exemplo abaixo mostra z >-0.8. Isso significa que você está procurando a probabilidade de que z é maior que -0.8, então você precisa desenhar uma linha vertical A -0.8 desvios padrão da média e sombrear tudo o que é maior do que esse número.

   

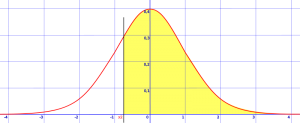
   área sombreada é z > -0.8

   Passo 2: Visite o normal de probabilidade do índice de área e encontrar uma imagem que se parece com o seu gráfico. Siga as instruções nessa página para encontrar o valor z para o grafo. O valor z é a probabilidade.

   Dica: O Passo 1 é tecnicamente opcional, mas é sempre uma boa ideia esboçar um gráfico quando se está a tentar responder a problemas de palavras de probabilidade. Isso porque a maioria dos erros acontecem não porque você não pode fazer a matemática ou ler uma tabela-z, mas porque você subtrai uma pontuação-z em vez de adicionar (ou seja, você imagina a probabilidade sob a curva na direção errada. Um esboço ajuda-o a cimentar na sua cabeça exactamente o que procura.se ainda tiver problemas, consulte os tutores em: Chegg.com os seus primeiros 30 minutos com um tutor ao vivo são grátis!

   problemas de Palavras de distribuição Normal

   Este vídeo mostra um exemplo de um problema de palavras de distribuição normal. Para mais exemplos, leia abaixo:

   por favor, aceite estatísticas, cookies de marketing para assistir este vídeo.

   Quando você lida com a distribuição normal em uma classe estatística, Você está tentando encontrar a área sob a curva. A área total é de 100% (em decimal, isto é 1). Problemas de distribuição normais vêm em seis tipos básicos. Como sabe que um problema de palavras envolve uma distribuição normal? Procure a frase chave “assumir que a variável é normalmente distribuída” ou “assumir que a variável é aproximadamente normal.”Para resolver um problema de palavras você precisa descobrir que tipo você tem. “entre”: Conter a frase “entre”e inclui um limite superior e inferior (ou seja,”encontrar o número de casas com preços entre $50K e 200K”).

4. “Mais do que” ou “acima”: conter a frase “mais do que” ou “acima”. “menos de”.
5. Corte Inferior Fora de Exemplo (vídeo)
6. Corte Superior Fora de Exemplo (vídeo)
7. Meio por Cento Exemplo (vídeo)

“Entre”

Este manual cobre a solução de problemas que contêm a expressão “entre” e inclui um limite superior e inferior (por exemplo, “encontrar o número de casas com preços entre us $50 mil e 200 mil”. Note que isto é diferente de encontrar a “porcentagem média” de algo.

problemas de palavras com a distribuição normal:” entre”: passos

Passo 1: Identificar as partes do problema da palavra. O problema da palavra identificará:

1. A Média (Média ou μ).desvio-padrão (σ).
2. número seleccionado (ou seja,” escolher um ao acaso “ou”seleccionar dez ao acaso”).
3. X: os números associados com ” entre “(ou seja,” entre US $5.000 e US $10.000 ” teria X como 5.000 e US $10.000).

:tamanho Da Amostra (400 casas, 33 pessoas, 99 fábricas, 378 Canalizadores, etc.).). Ou

Passo 2: desenhar um gráfico. Põe o meio que identificaste no Passo 1 no centro. Put the number associated with “between” on the graph (take a guess at where the numbers would fall–it doesn’t have to be exact). Por exemplo, se a sua média foi de us $100, e você foi convidado para a “hora de salários entre us $75 e us $125”), o gráfico será algo parecido com isso:

Passo 3:calcular o z-scores. Plug the first X value (in my graph above, it’S 75) into the z value formula and solve. O μ (a média), é 100 do grafo de amostra. Você pode obter estes números (incluindo σ, o desvio padrão) de suas respostas no Passo 1 :

Passo 4: repetir o Passo 3 para o segundo X.

Passo 5: retirar os números dos passos 3 e 4 e usá-los para encontrar a área na tabela Z. se lhe foi pedido para encontrar uma probabilidade na sua pergunta, vá para o passo 6a. se lhe foi pedido para encontrar um número de um dado Tamanho de amostra específico, vá para o passo 6b.

passo 6a:converter a resposta do Passo 5 numa percentagem. por exemplo, 0, 1293 é 12, 93%.é isso-saltar o passo 6b!

passo 6b

multiplique o tamanho da amostra (encontrado no Passo 1) pelo valor z que encontrou no Passo 4. Por exemplo, 0,300 * 100 = 30.é isso!

” More Than “or” Above “

This how-to covers solving normal distribution problems that contain the phrase ” more than “(or a phrase like”above”).

Passo 1: dividir o problema da palavra em partes. Encontrar:

1. A Média (Média ou μ)
2. o desvio-padrão (σ)
3. um número (por exemplo, “escolha cinqüenta ao acaso” ou “selecione 90 ao acaso”)
4. X: o número associado com a declaração “menos de”. Por exemplo, se você foi convidado a encontrar “menos de $9,999” então X é 9,999.

Passo 2: Encontrar a amostra do problema. Você terá um tamanho específico (como” 1000 televisões”) ou uma amostra geral (“cada televisão”).

desenhe uma imagem se o problema com a média e a área que você está procurando. Por exemplo, se a média é de r $15, e foram convidados a encontrar o que jantares custar mais do que us $10, o gráfico pode parecer como este:

Passo 3: Calcular o z-score (plug seus valores para o valor de z fórmula e resolver). Use as suas respostas do Passo 1 :

basicamente, tudo o que está a fazer com a fórmula é subtrair a média de X e depois dividir essa resposta pelo desvio-padrão.

Passo 4: Encontre a área usando a pontuação z do Passo 3. Usa a mesa Z. Não sabes ler uma mesa-z? Veja o vídeo na página da z-table.

Passo 6: Vá para o passo 6a para encontrar uma probabilidade ou vá para o passo 6b para calcular um determinado número ou quantidade.

passo 6a
transformar a resposta do Passo 5 numa percentagem.por exemplo, 0.1293 é 12,93%.passo 6b: acabou!

passo 6b
multiplique o tamanho da amostra do Passo 1 pela pontuação z do Passo 4. Por exemplo, 0,500 * 100 = 50.acabou!

inferior a

This how-to covers solving normal distribution word problems that have the phrase ” less than “(or a similar phrase such as”less than”).

normal distribution word problems less than: Steps

Step 1: Break up the word problem into parts:

1. The mean (average or μ)
2. Standard deviation (σ)
3. número seleccionado (i.e. “escolha um ao acaso “ou”selecione dez ao acaso”)
4. X: o número que vai com ” menos de “(ou seja, “abaixo de $99.000” listaria X como 99.000)

Mais, você terá:

1. um tamanho de amostra específico. Por exemplo, 500 barcos, 250 sanduíches, 100 televisões, etc.
2. todos na amostra (ser-lhe-á pedido para encontrar uma probabilidade). Por exemplo,” estudantes de Medicina do primeiro ano”,” pacientes com cancro “ou” pilotos de linha aérea”.”

Passo 2: Desenhe uma imagem para ajudá-lo a visualizar o problema. O gráfico seguinte mostra uma média de 15, e uma área “abaixo de 4”):

Passo 3: Encontrar o valor de z conectando os valores dados na fórmula. O” X ” em nosso grafo de amostra é 4, e O μ (Ou média) é 15. Você pode obter estas figuras (incluindo σ, o desvio padrão) a partir de suas respostas na etapa 1, onde você identificou as partes do problema:

Tudo o que você precisa fazer para resolver a fórmula é:

1. subtrair a média de X.
2. dividir pelo desvio-padrão.

Passo 4: tome o número do Passo 3, em seguida, use a tabela z para encontrar a área.

Passo 5: para encontrar uma probabilidade, vá para o passo 6a. para encontrar um número de um dado Tamanho de amostra específico, vá para o passo 6b.

passo 6a

mude o número do Passo 5 para a percentagem. por exemplo, 0.1293 é 12,93%.é isso!

passo 6b

multiplique o tamanho da amostra (encontrado no Passo 1) pelo valor z que encontrou no Passo 4. Por exemplo, 0,300 * 100 = 30.é isso!

corte inferior

às vezes, em um problema de palavra de distribuição normal, ser-lhe-á pedido para encontrar um “limite inferior de uma percentagem superior” de algo (ou seja, “encontrar o ponto de corte para passar por um determinado exame onde os 40% superiores dos tomadores de teste passam”). Um ponto de corte inferior é o ponto em que as pontuações cairão abaixo desse ponto. Por exemplo, você pode querer encontrar onde o ponto de corte é para o fundo 10% dos participantes do teste.

por favor, aceite estatísticas, cookies de marketing para ver este vídeo.

confira nosso canal do YouTube para mais problemas trabalhados.

distribuição Normal TI 89 exemplos

em estatísticas elementares, você muitas vezes será confrontado com uma pergunta que lhe pergunta os pontos de corte para uma determinada percentagem da distribuição normal, como o Top 90% ou o top 10%. Enquanto resolver estes tipos de problemas à mão é complicado, a calculadora de gráficos TI-89 faz um trabalho leve de encontrar pontos de corte para uma porcentagem superior com a função normal inversa. O que você está realmente fazendo é procurar os pontos de corte para um determinado percentil: por exemplo, se você tem uma lista de notas e você quer saber qual é a pontuação no percentil 99, você pode usar a função normal inversa para encontrar esse ponto de corte percentual.

encontrar pontos de corte para uma porcentagem superior

problema de amostra: estudantes em uma determinada faculdade média de 5 pés 8 polegadas (68 polegadas) de altura. As alturas são normalmente distribuídas, com um desvio padrão de 2,5 polegadas. Qual é o valor que separa os 1% mais altos das alturas do resto da população?

Passo 1: Carregue em aplicações e use as teclas de posicionamento para realçar o Editor de Estatísticas / listas.Passo 2: Carregue em F5 2 1 (isto leva-o ao ecrã normal inverso).

Step 3: Enter 0.99 na área box.Passo 4: introduzir 68 na caixa μ.

Passo 5: indicar 2, 5 na caixa σ.Passo 6: pressione ENTER.

Passo 7: Leia os resultados: inverso = 73.8159 significa que a altura de corte para o percentil 99 é de 73.8159 polegadas.é isso!exemplo de proporção de probabilidade (função NormalCDF)

questão da amostra: Um grupo de estudantes com salários normalmente distribuídos ganham uma média de US $6.800 com um desvio padrão de US $2.500. Que proporção de estudantes ganha entre $ 6,500 e $ 7,300?Passo 1: Press APPS. Vá para o Editor de Estatísticas/listas e carregue em ENTER.Passo 2: pressione F5 4.

Passo 3: indique 6500 na caixa de valores mais baixos.

Passo 4: introduzir 7300 na caixa do valor superior.

Passo 5: inserir 6800 na caixa μ.

Passo 6: indicar 2500 na caixa σ. Pressione ENTER.Passo 7: Leia a resposta. Cdf=.127018. Por outras palavras,013, ou 13% dos estudantes ganham entre $ 6.500 e $7.300.

TI-89 Graficando uma curva de distribuição Normal

o TI-89 não só pode calcular as pontuações z e os valores de retorno para as distribuições normais, como também pode graficar a curva de distribuição normal. Graficar uma distribuição normal pode ajudá-lo a ver o que é que deveria estar à procura, e dá-lhe mais uma ferramenta para resolver problemas de distribuição normais. O TI-89 pode apresentar uma curva de distribuição normal com uma área sombreada para qualquer valor. Por exemplo, você pode criar um gráfico que é: menor que um determinado número, maior que um determinado número, ou entre um determinado conjunto de números.problema da amostra: desenhar uma curva de distribuição normal para os salários dos estudantes durante um semestre típico. Os salários dos estudantes têm uma média de $6.800 e desvio padrão de $ 2.500 . Sombrear a área no gráfico que corresponde a salários entre US $ 7.300 e US $ 9.000.

Passo 1: Carregue em aplicações e seleccione o Editor de Estatísticas/listas.

Step 2: Press F2 3 and F2 4.

Passo 3: Press F5) 1.

Passo 4: role para baixo e introduza 7300 na caixa de valores mais baixos.

Passo 5: role para baixo e indique 9000 na caixa do valor superior.

Passo 6: role para baixo e introduza 6800 na caixa μ.

Passo 7: deslocar para baixo e introduzir 2500 na caixa σ.

Passo 8: deslocar para baixo. Rode a escala automática para ” Sim “se carregar na tecla de posicionamento direito, em seguida, a tecla de posicionamento para baixo para seleccionar “Sim”. Pressione ENTER.

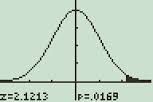
um grafo de distribuição normal apresentado na calculadora TI-89.é isso!dica: Se quiser introduzir ∞ (infinity) como um dos seus valores mais baixos ou superiores, carregue na tecla diamond e depois catalogue.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 533-534, 1987.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” the Error Curve.”§6.4 in Mathematical Recreations. New York: W. W. Norton, pp. 121-123, 1942.
Patel, J. K. and Read, C. B. Manual da distribuição Normal. New York: Dekker, 1982.Qual é a regra 68-95-99.7?

Box transformação de Cox transformação

Box transformação de Muller modelos de mistura Gaussiana.o que é um gráfico de probabilidade Normal?

Como calcular uma pontuação Z nas estatísticas

Encontre a área à direita de uma pontuação Z.

usando a aproximação Normal para resolver um problema Binomial

Qual é o Fator de correção da continuidade?

área sob uma curva de distribuição Normal Índice

Teorema do Limite Central.

A distribuição normal distorcida.curva normal de duas caudas.

A função Q.

CITE isto como:
Stephanie Glen. “Distribuições normais (curva de Bell): definição, problemas de palavra” de StatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/probability-and-statistics/normal-distributions/

——————————————————————————

Necessita de ajuda com a lição de casa, ou a pergunta de teste? Com o estudo Chegg, você pode obter soluções passo a passo para suas perguntas de um especialista no campo. Os seus primeiros 30 minutos com um tutor Chegg são grátis!