Maximum Parsimony on Phylogenetic networks

Definition of phylogenetic networks

we follow the definition of the phylogenetic networks as given in , Definition 4, page 16]. Para todas as outras definições graph-theoretical que não são dadas aqui, nós seguimos . Uma rede filogenética enraizada, simplesmente chamada aqui de rede filogenética, é definida como um grafo acíclico enraizado (DAG), cuja raiz tem indegree 0 e as folhas têm outdegree 0. Os vértices cuja indegree é maior que 1 são chamados vértices reticulados e as arestas com vértices reticulados como vértices da cabeça são chamadas arestas reticuladas. Todas as outras arestas são denominadas arestas de árvores. A definição dada em Toma conta da retenção de “tempo-consistência”, ou seja, que as arestas das árvores ocorrem em um tempo positivo e os vértices reticulados têm pais que só podem”coexistir no tempo”. Assim, para a frente, lembramos a definição formal de redes filogenéticas como dado em .

dado qualquer grafo dirigido, dizemos que dois vértices u E v não podem coexistir no tempo se existe uma sequência P = (p1, p2,…, p k ) de caminhos em N tal que:

1. p i é dirigido caminho que contém pelo menos uma árvore de ponta, para cada 1 ≤ i ≤ k,

2. u é a cauda de p 1, e v é o chefe de p, k , e

3. para cada 1 ≤ i ≤ k – 1, existe uma rede de vértices cujos dois pais são a cabeça p eu e a cauda de p i+1.

uma rede filogenética N é uma DAG enraizada obedecendo às seguintes restrições::

1. cada vértice tem indegree e outdegree definidos por uma das quatro combinações (0, 2), (1, 0), (1, 2), ou (2, 1) – correspondendo a, respectivamente, raiz, folhas, vértices de árvore internos, e vértices reticulados. Todos os vértices, exceto os vértices reticulados, são chamados vértices de árvore.

2. Se dois vértices u E v não podem coexistir no tempo, então não existe um vértice de rede w Com arestas (u, w) E (v, w).

3. dada qualquer aresta da Rede, pelo menos um dos seus endpoints deve ser um vértice de árvore.

outro componente desta definição é que para qualquer aresta na rede filogenética, pelo menos um de seus pontos finais (ou a cabeça ou cauda) é um vértice de árvore. Aqui, vamos usar esta definição. Sempre que possível, salientamos se as condições da definição são necessárias.

redes filogenéticas podem ser vistas ingenuamente como uma rede que contém como subgrafos, as árvores que explicam as histórias evolutivas de diferentes segmentos das sequências terminais de entrada. Dada uma rede filogenética, excluir um de cada incidente de aresta para um vértice reticular não garante uma árvore filogenética resultante com o mesmo conjunto de folhas que a da rede. Esta é uma propriedade indesejável, especialmente se o critério de parsimonia é definido por encontrar uma árvore filogenética dentro da rede que é mais parsimônica para o dado site, como definido em . A fim de evitar este problema, é necessário assumir que nenhum vértice interno tem duas crianças reticuladas. Nós chamamos esta classe de redes filogenéticas como uma rede filogenética sem reticulações irmãs. Veja a Figura 1 para alguns exemplos de redes filogenéticas.

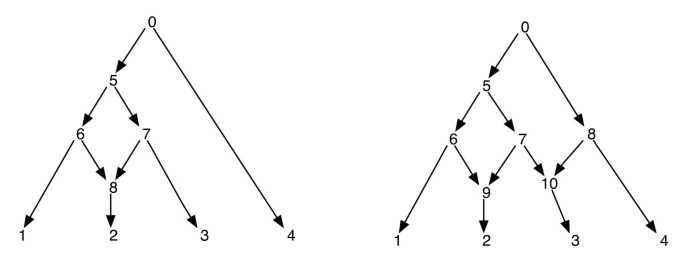
Filogenética Redes. A figura mostra duas redes filogenéticas; a da esquerda tem apenas um vértice reticular e a da direita tem dois vértices reticulados que são irmãs uma da outra. Note que remover as arestas (7, 9) e (7, 10) da rede à direita não resulta em uma árvore onde o vértice 7 é uma folha. Isto mostra que remover uma aresta de entrada cada vértice reticular não necessariamente produz uma árvore com o mesmo conjunto de folhas que a rede. O pós-encomenda e a pré-ordenação dos vértices da rede de esquerda são 1, 2, 8, 6, 3, 7, 5, 4, 0 e 0, 5, 6, 1, 8, 2, 7, 3, 4 respectivamente e para a rede à direita, eles são 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 e 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respectivamente.

Antes de avançarmos para a definição dos problemas de parsimonia, a seguinte é uma observação útil. Para um filogenética de rede N sem irmã reticulations, e ter r reticulada vértices e com folha conjunto X, denotamos T ( N ) como o conjunto de todas as árvores contidas no N. Cada árvore é obtida seguindo dois passos: (1) para cada reticulado vértice, remover uma entrada de bordas e, em seguida, (2) para cada vértice v de indegree e outdegree 1, cujo pai é u e a criança é w, o contrato de arestas (u, v) e (v, w) em uma única aresta (u, w). A condição que cada aresta em N tem um vértice de árvore como um endpoint e que cada vértice de árvore tem pelo menos um vértice de árvore como uma criança, garante que o conjunto de folhas da árvore resultante é o mesmo que o da rede. Daí o conjunto T ( N ) contém exatamente 2rphylogenetic árvores, cujas folhas conjunto é exatamente X.

Máxima Parcimônia

Nós nos referimos, os leitores para uma descrição geral da ideia de parcimônia e para a discussão de vários parcimônia algoritmos. It has been pointed in that the parsimony method for trees can be extended to phylogenetic networks. Em uma série de artigos , um tal parcimônia e critério é definido por encontrar uma árvore na rede que tem a melhor pontuação parcimoniosa, e algoritmos eficientes para otimizar este critério em um determinado filogenética de rede têm sido desenvolvidos. Embora estes algoritmos sejam mostrados para executar bem na prática, eles podem executar corretamente apenas para redes filogenéticas sem reticulações irmãs, uma vez que é fácil de procurar por uma árvore ideal nesta classe restrita de redes. Nesta seção, Nós declaramos uma versão alternativa do problema de parsimonia e nas seguintes seções fornecem algumas soluções heurísticas para otimizar a pontuação em qualquer rede filogenética.

Let = {1, 2,…, n} denote o conjunto de etiquetas de folhas de uma dada rede filogenética N. A função λ: → {0, 1, …, / Σ / – 1} é chamada de função de atribuição de Estado sobre o alfabeto Σ (Um conjunto não-vazio) para N. dizemos que uma função λ ^ :V (N ) → { 0 , 1 , … , | Σ / – 1 } é uma extensão de λ EM N se concordar com λ nas folhas de N. Para um vértice v em N, chamamos λ ^ (v) como uma atribuição de λ ^ em v. uma rede totalmente atribuída é uma rede na qual todos os vértices têm etiquetas de {0, 1, …, |Σ| – 1}. Se e = (u, v) é uma aresta em N, onde u é o pai de v, nós denotamos w e ( λ) ^ c i j , onde i = λ ^ ( u) e j= λ ^ ( v). Para um grafo G, nós deixamos E (G) denotar o conjunto de arestas de G. então o problema de parsimonia é definido como segue.

entrada: Um filogenética de rede N com folha de etiquetas e um estado de atribuição de função de λ sobre o alfabeto Σ de N.

Parcimônia e critério: Para uma extensão λ ^ de λ, deixe

e

Saída: dado P ∈ {P1, P2}, encontre λ ^ que minimize P ( λ ^ ) .

notamos que p 1 (λ^) é introduzido e p 2 (λ^) é a definição que utilizaremos neste papel. Uma abordagem mais geral é minimizar Q ( λ ^ ) = ∑ e ∈ E ( N ) d e ( w e ( λ ^ ) ) , onde d é um não-negativo função de peso nas bordas de N. Para os fins deste artigo, vamos nos restringir P = P2, embora a primeira das nossas abordagens, a programação dinâmica solução também vale para P = Q.

Parcimônia algoritmos em redes

Atravessando um filogenética de rede

Em uma rede, vértice transversal refere-se ao processo de visita cada vértice exatamente uma vez, de uma forma sistemática. Tais traversais são classificados pela ordem na qual os vértices são visitados. Precisamos de dois tipos de passagens de vértices de rede para descrever nossos algoritmos. Estas são bem conhecidas pelas árvores filogenéticas, e as apresentamos aqui para redes filogenéticas. Os algoritmos para os traversais indicados abaixo começam a partir de qualquer vértice V dado na rede. Neste artigo, sempre realizaremos os traversais do vértice raiz da rede.

passagem de pré-ordem de uma rede filogenética de um vértice v

1. visita o vértice v.

2. executa recursivamente a passagem de pré-ordem de cada criança que ainda não foi visitada.

post-order traversal of a phylogenetic network from a vertex v

1. Recursively perform post-order traversal from each child that has not yet been visited.

2. visite o vértice v.

Uma vez que uma rede filogenética é um DAG, tais traversais visitarão todos os vértices da rede exatamente uma vez. (Ver para mais detalhes sobre a existência em tais traversais em DAGs). Para os propósitos deste artigo, assumimos que os vértices de uma rede são rotulados exclusivamente por inteiros. Note que as folhas já estão rotuladas a partir do conjunto ; e então usamos outros inteiros para outros vértices. Sempre que os vértices – criança de v são extraídos, eles também são dispostos em ordem crescente de seus labelings inteiros e os traversais pré e pós-ordem são realizados nesta ordem. Isto irá assegurar o seguinte: se os vértices v e v’ são tais que não há direcionado caminho entre eles, então o vértice v é percorrido antes de vértices v’ em pré-ordem se, e somente se o vértice v é percorrido antes do vértice v’ em pós-ordem. Veja a Figura 1 para alguns exemplos. Com esta propriedade, notamos que os traversais pré e pós – ordem da raiz de uma rede filogenética cada um traçam a mesma árvore, que chamamos aqui de árvore transversal.

solução de Programação Dinâmica

programação dinâmica é usada para fornecer soluções eficientes para encontrar a pontuação exacta de parsimonia quando a rede é uma árvore filogenética . Nesta seção, mostramos que a mesma abordagem pode ser generalizada às redes filogenéticas. Sankoff do algoritmo em uma árvore atravessa os vértices da árvore através de pós-ordem, enquanto computação o mínimo de custos de cada estado em cada vértice das folhas para a raiz e, em seguida, escolhe o melhor atribuições de cada vértice pelo retrocesso da raiz para as folhas, percorrendo a árvore de vértices através de pré-encomenda. Ambas as fases são apresentadas para redes em algoritmos 1 e 2, respectivamente. DescrevemO-los brevemente abaixo. Pode-se notar que se a rede é uma árvore, então nossos algoritmos coincidem com as fases de pré-ordem e pós-ordem do método de Sankoff para árvores.

dada uma rede filogenética N, com vértices de folha rotulados e com função de atribuição de Estado λ sobre o alfabeto Σ, atribuir a cada vértice V a V uma quantidade S v (i) para cada i ∈ Σ. Em árvores filogenéticas, S v (i) denota a soma mínima de custos de todos os Eventos do vértice v para todas as folhas que são alcançáveis a partir de v, dado que v é atribuído estado i e todos os vértices descendentes de v são atribuídos a cada um um um estado. Em redes, não há uma maneira simples de calcular tal quantidade. Em vez disso, permitimos que s v (i) seja um limite inferior da pontuação exata acima e é calculado durante a fase transversal pós-ordem.se v é uma folha de N, então S v (i) é atribuído 0 se o estado observado é estado i, e infinito de outra forma. Agora tudo o que precisamos é de uma relação recursiva para calcular S v (i) para o resto dos vértices. Para cada criança W de v, dizemos w satisfaz a condição de travessia pós-ordem em relação a v, ou simplesmente condição de travessia em relação a v em vista da observação no início desta seção, se o seguinte:

1. (i)

   O vértice w é um reticulado de vértices e

2. (ii)

   se v’ é o pai de w que n ao v, então o vértice v tem de ser percorrido antes de v’, em pós-ordem a passagem de N.

Vamos agora definir recursivamente para cada aresta (v, w),

Para uma árvore filogenética, s(v, w)(i) assume sempre a primeira destas quantidades, e, assim, dá a soma dos custos de substituição ao longo das bordas da árvore que se situam abaixo do vértice v, desde que o vértice v é atribuído o estado que eu. Para filogenética redes, para que os custos de substituição ao longo das bordas que se encontram abaixo de um reticulado vértice w apenas uma única vez quando vértice v é atribuído o estado que eu, nós deixamos o ‘pai’ v de w na transversal da árvore de conta por todos os custos de substituição ao longo de todas as arestas que se encontram abaixo v. Por outro lado, se v não é um pai de w na árvore transversal, s(v, w)(i) simplesmente denota o custo de substituição do estado I no vértice v para outro estado em w que é menos caro.

definimos então

onde a soma corre para todas as crianças(ren) vertex(S) w de v. Como mencionado anteriormente, em árvores filogenéticas, S v (i) denota a soma mínima possível de custos de substituição ao longo de todas as arestas do vértice v para todas as folhas que são alcançáveis a partir de v, dado que v é atribuído estado i e todos os vértices alcançáveis a partir de v são atribuídos a cada um um estado.

em redes filogenéticas, ao calcular s(v, w) (i) onde w é um vértice reticular tal que (v, w) não é uma aresta na árvore transversal, não há conhecimento prévio do Estado que será posteriormente atribuído no vértice reticular W. Assim, s(v, w)(i) só pode ser um limite inferior das bordas da rede, que se situam abaixo do vértice v, se o vértice v é atribuído o estado que eu. A razão para isso é que s(v, w)(i) é a substituição de custo a partir do estado i no vértice v para outro estado em w que é menos caro, em vez da substituição custos a partir do estado i no v para o estado do w que serão atribuídos mais tarde. Uma vez que a definição de s v (i) depende da definição de s(v, w) (i), e eles são definidos recursivamente, observamos o seguinte:: S v (i) é um limite inferior sobre a soma dos custos de substituição ao longo das bordas da rede que são acessíveis a partir do vértice v, desde que v é atribuído ao estado e a todos os descendentes a árvore vértices são atribuídos a um único estado, e o reticulado vértices são atribuídos dois estados que não são necessariamente as mesmas. Os Estados atribuídos do vértice reticular contribui para um conflito se os estados não são os mesmos. Vamos supor que o estado i é atribuído ao vértice R raiz, e todos os vértices de árvore são atribuídos um estado único, enquanto os vértices reticulados são atribuídos dois estados. Em seguida, o custo de S r (i) denota o mínimo possível a soma dos custos de substituição ao longo de todas as arestas de uma transversal da árvore com um dos estados atribuídos para reticulada vértices, mais a soma dos custos de substituição ao longo do restante reticulada bordas com a alternativa de atribuição de estado no reticulado vértices. Uma vez que buscamos uma atribuição nos vértices da rede sem conflitos nos vértices reticulados, S r (i) é um limite inferior no custo de tal atribuição onde o vértice raiz é atribuído i e todos os vértices são atribuídos com uma atribuição única.

durante esta fase, também armazenamos os Estados

para ser capaz de retroceder o estado de w que atinge a quantidade s(v, w) (i) durante a fase de pré-encomenda. Ver Algoritmo 1.

Fase transversal de pré-ordem: primeiro escolhemos o mínimo

onde R é o vértice raiz e atribuímos o estado que atinge o mínimo no vértice raiz, i.e., deixe λ ^ ( r ) = i r tal que r (i r ) = S. Para qualquer outro vértice w que não é um reticulado vértice, cujo pai v já está atribuída, com o estado i, que atribui ao estado t(v, w)(i). Para um vértice reticular w cujos vértices-mãe São v e v’, vamos supor que v e v’ são atribuídos Estados I e i’ respectivamente quando atravessando pela pre-ordem. Os possíveis estados j = t (v, w) (i) E j’ = t(v’, w) (i’) de w que atingem s(v, w) (i) E S(v’, w) (i’), respectivamente, não precisam ser os mesmos. Em outras palavras, é possível que j ≠ j’. Neste caso, temos um conflito no reticulado vértice w. Assim, a técnica de programação dinâmica não consegue dar uma extensão para λ cujo parcimônia pontuação S. neste caso, podemos simplesmente escolher entre j e j’ para λ(w) de acordo com a qual os vértices entre v e v’ é atravessada primeiro em pré-ordem. Assim, se o vértice w satisfaz a condição transversal em relação a v temos λ ^ (w ) =J.

Após completar a fase de pré-ordem, podemos obter a pontuação correspondente à Extensão λ ^ pela primeira configuração S ‘= S e atualização S’ em cada vértice reticular W como se segue: A pontuação do limite superior S’ é actualizada, correspondendo à atribuição j no vértice w como S’ – c i’ j’ +c i ‘ J. Ver Algoritmo 2. A figura 2 mostra um exemplo de como o algoritmo corre em uma rede. Uma vez que S r (i) é um limite inferior na atribuição ideal onde o vértice raiz é atribuído i e todos os vértices são atribuídos com uma atribuição única, e desde s = min i s r (i), concluímos que S é um limite inferior do ótimo que procuramos encontrar. Veja lema 1 para uma prova formal.

Dinâmica de solução de programação. A solução de programação dinâmica aplicada a uma rede filogenética. Os estados são 0, 1 e 2. A matriz de custos usado tem todos os 1s, exceto os elementos da diagonal, que são todos os 0s. As tabelas mostradas em cada vértice v são os custos, S v (i) (segunda linha) de cada estado, eu (primeira linha) que são calculados durante o pós-order traversal. Também são mostrados no vértices são os estados do filho w, a saber, a t(v, w)(i) (terceira linha), que correspondem aos custos na segunda linha; quando houver dois filhos para um vértice, as entradas na terceira linha são representados por um par de estados do filho à esquerda e à direita da criança, respectivamente. Cada aresta (v, w) é rotulado com s(v, w) (i) para cada Estado I. Durante a passagem de pré-ordem, os estados para cada vértice são selecionados (mostrado em negrito). O custo de 2 realçado em negrito no vértice raiz dá um limite inferior, S. O estado atribuído em cada vértice é realçado em negrito. O algoritmo encontra um total de três substituições (realçadas por arestas a negrito). Isto é porque os Estados atribuídos nos vértices-mãe do vértice reticular dão atribuições conflitantes de 1 e 2 respectivamente, dos quais o estado 1 é atribuído no vértice reticular. Assim, com um custo extra de 1, obtemos a pontuação de 3 (um limite superior da pontuação óptima) como a pontuação parsimónica correspondente à atribuição mostrada. Observe que o ideal de parcimônia de pontuação na rede é de 2 (igual ao limite inferior), que pode ser encontrado por busca exaustiva e pode ser realizado alterando a atribuição de 1 para 2 para a esquerda pai do reticulado de vértices e de 1 para 2 para o reticulado de vértices. Assim, o limite inferior corresponde com a pontuação ótima, embora a atribuição correspondente ao limite inferior não seja livre de conflitos e não o mesmo que a atribuição correspondente ao ótimo.

Lema 1. The quantity S is a lower bound of the optimum parsimony score on the network N.

Proof. Pela construção de S, temos

, onde o segundo summand é para o reticulado vértice w com os pais sejam v e v’, tais que v satisfaz a travessia condição de w.r.t. w. Assim, o custo c λ ^ ( v ) , λ ^ ( w ) é a substituição de custo atribuído estado λ ^ ( v ) em v para o estado λ ^ ( w ) para w. Por outro lado, o custo c λ ^ ( v ) , t ( v ‘, w ) ( λ ^ ( v ‘) ) é a substituição de custo atribuído estado λ ^ ( v ) em v para o estado t ( v ‘, w ) ( λ ^ ( v ‘ ) ) em w. Nota-se que o estado t ( v ‘, w ) ( λ ^ ( v ‘ ) ) não é necessariamente o mesmo que o estado λ ^ ( w ) , e S é o mínimo entre todas as atribuições que pode resultar em conflitos no reticulado vértices.

Suponha Que s ^ é a pontuação parsimónica óptima em N com a função μ: V (N) → {0, 1, …, / Σ / – 1} como a extensão de λ temos

onde na segunda soma w é um vértice reticular com os pais v e v’. Uma vez que μ é uma atribuição livre de conflitos que está contida no conjunto de todas as atribuições entre cujos custos S é o mínimo (comparar equação (3) e (4)) Temos s≤ s ^ . D

agora para a complexidade do algoritmo. Suponha que a rede n tem n folhas e R reticulados vértices. Então o número de vértices em N é 2(n + r) -1. Em cada vértice v e para cada Estado i, a quantidade S pode ser calculada em O(k2) tempo, em que k = |Σ|. A etapa transversal de pré-ordem envolve encontrar S em complexidade O (k) e atribuir os melhores estados para cada vértice. Além disso, a fixação de Estados reticulados conflitantes de vértices leva O(r) tempo. Assim, a complexidade do algoritmo (apresentada aqui)para encontrar um limite inferior e superior é O((n + r) k2). Um limite superior alternativo pode ser obtido em O(nk2) simplesmente atribuindo durante a fase transversal pós-ordem, para cada vértice reticular o estado que ocorre o número máximo de vezes nas folhas alcançáveis a partir do respectivo vértice reticular; e procedendo através de encontrar S v (i) para os vértices restantes. A melhor situação também pode ser obtido por restringir os estados possíveis para um único estado para cada reticulado vértice, executando o algoritmo de programação dinâmica para cada um dos kr combinações de estados para o reticulado vértices, e escolhendo o mínimo entre todos eles. A complexidade temporal deste processo é O (nkr+2).

Algoritmo 1 Post-order traversal fase: Calcular o custo de cada estado em cada vértice

1. 1:

   Entrada de dados: Rede N e o observado estados a partir de Σ em folhas de N, isto é, um estado de atribuição de função de λ sobre o alfabeto Σ de N.

2. 2:

   Para cada folha de v, let’S v (i) = 0 se λ(v) = i = e ∞ no caso contrário.

3. 3:

   repetir em pós-ordem para cada vértice interno (vértice da raiz, vértice da árvore interna ou vértice reticular) v em N: Para cada Estado i, calcular S v (i) dado em (1) e t(v, w) (i) para cada criança w de v, dado em (2).

4. 4:

   Saída: {(s v (i),): v ∈ V (N), i.Σ}.

Minimizar o número de mutações em um filogenética de rede

O algoritmo de Fitch conta o número de alterações feitas em um bifurcating árvore filogenética para qualquer conjunto de caracteres, onde os estados podem alterar de qualquer estado para qualquer outro estado. Assim, a matriz de custo é tal que seus elementos diagonais são todos zeros e os elementos fora-diagonais são todos uns. Nesta seção, mostramos como o algoritmo de Fitch se estende até encontrar limites superiores e inferiores para o número de mudanças evolutivas em uma dada rede filogenética. Primeiro, mostramos que o algoritmo Fitch pode ser estendido para dar um limite superior para a pontuação ideal parsimonia. Como antes, as fases de pós-ordem e pré-ordem são dadas em algoritmos 3 e 4 abaixo. Ver Figura 3 para um exemplo de execução do algoritmo.

Fitch-tipo de solução. A solução do tipo Fitch aplicada à mesma rede filogenética e os dados da folha na Figura 2. A cada vértice é atribuído um conjunto de todos os estados possíveis, juntamente com uma pontuação quando os vértices da rede são atravessados em pós-ordem. A pontuação na raiz dá um limite superior para a pontuação ideal. As atribuições de estado são dadas durante a fase de pré-ordem transversal e o número de substituições corresponde com a pontuação na raiz.

algoritmo 2 fase transversal de pré-ordem: Calcular os limites inferior e superior do óptimo e a atribuição correspondente do limite superior

1. 1:

   Input: {(s v (i), ): v ∈ V (N), i ∈ Σ}.

2. 2:

   Let s = min i s r (i), em que r é o vértice raiz e Let λ ^ ( r ) =arg min i s r ( i ) .

3. 3:

   Deixe-S’ = S

4. 4:

   Para cada vértice w em pré-ordem cuja principal vértice v imediatamente antecede w em pré-ordem, deixe λ ^ ( ω ) = t v , w ( i ) , onde i= λ ^ ( v ) .

5. 5:

   Visite cada reticulado vértice w com os pais, v e v’ tal que w satisfaz a travessia condição com respeito a v, com i= λ ^ ( v ) , i ‘= λ ^ ( v ‘) , j ‘= t ( v ‘, w ) ( i ) e atualização de S’ como a seguir:

   S ‘← S ‘- c i ‘ j ‘+ c e i ‘ j .
6. 6:

   resultado: (limite inferior, limite superior) = (S, S’); extensão correspondente à pontuação S ‘ : λ ^ .

algoritmo 3 fase transversal pós-ordem: calcular a melhor

1. 1:

   entrada: Rede filogenética n e uma função de atribuição de Estado λ sobre o alfabeto Σ Para N.

2. 2:

   para cada folha v de N, é-nos dado um(v) = {λ(v)}, um conjunto singleton contendo o estado observado na folha.

3. 3:

   Set UB = 0.

4. 4:

   Recurse pós-ordem: Para um vértice v de T com crianças w1 e w2, e Se o vértice v tem um único filho, w,

e