Heresy comes in different levels. Para o intelectual moderno, os níveis mais baixos de heresia podem ser sobre política ou economia – áreas de pensamento onde você pode ter ideias pouco ortodoxas sem ser excluído de uma companhia educada. Níveis mais altos de heresia podem ser sobre religião ou ciência – discordar de suposições ortodoxas aqui, e você será visto como completamente-possivelmente-louco. O mais alto nível de heresia no mundo moderno é a heresia matemática. Discordância com a ortodoxia matemática é sinônimo de ” ser uma manivela completa.”Você simplesmente não tem permissão para duvidar de certas idéias em matemática sem ser condenado como um leproso intelectual.
infelizmente, como em qualquer outra área do pensamento, há uma relação inversa entre” aceitabilidade de desacordo “e” probabilidade de erro”.”Quanto mais tabu é desafiar uma suposição, mais provável ele vai entrar em colapso sob escrutínio. Os teólogos podem tolerar discordâncias sobre as propriedades de Deus, mas não podem tolerar discordâncias sobre a existência de Deus. A sua existência é demasiado fundamental para ser revista. Se Deus não existe, toda a estrutura teórica construída sobre esta suposição é destruída.assim é com a matemática. Várias suposições fundamentais não podem ser desafiadas e, portanto, transformaram-se em dogma, o que torna este artigo heresia matemática.
examinei os fundamentos da geometria padrão e encontrei dois erros-um lógico, o outro metafísico. Este artigo vai se concentrar no metafísico. Objetos essenciais descritos por matemáticos não existem. Assim, quaisquer conclusões que sejam derivadas com base na existência desses objetos são provavelmente incorretas.
neste caso, a alegação universalmente aceita de que “Pi é um número irracional e transcendental cuja magnitude não pode ser expressa por expansão decimal finita” é falsa por causa de um erro metafísico.
Pi é um número racional com expansão decimal finita. Esta ideia, que pode parecer inconcebível no início, irá revelar-se esmagadoramente razoável no final deste artigo.
(para o resto deste artigo, vou abreviar “Pi é um número racional com expansão decimal finita “como” Pi é um número finito “ou mais simplesmente,” Pi é finito.”)
sobre formas
minhas alegações são diretas e preservam a intuição geométrica básica. Por exemplo, este é um “círculo”:

esta é uma “linha”:

E estes são os “pontos”:

Se você acredita que esses objetos são de fato círculos, linhas e pontos, então você também acredita que pi é finito. Os matemáticos não acreditam que estes objectos se qualificam como” linhas “ou ” pontos”.”Em suas mentes, linhas e pontos não podem ser vistos, e de fato, eles diriam que as “linhas e pontos” acima são meras aproximações imperfeitas de linhas e pontos.
para entender por que, temos que fazer um conjunto de perguntas cujas respostas as pessoas assumem já ter sido resolvido. Estas são perguntas que supostamente são tão óbvias que não valem a pena fazer. E no entanto, quando lhes perguntamos aos matemáticos, obtemos respostas duvidosas. Perguntas como:
O que é uma “forma”?o que é uma”linha”?o que é um”ponto”?o que é um”círculo”?o que é”Distância”?faça essas perguntas ao seu intelectual médio, e provavelmente eles zombarão de você, porque eles assumem: “todo mundo sabe o que é uma linha!”Eles estão errados. Eu, por exemplo, acho que os matemáticos não sabem quais são as linhas. E porque suas teorias são construídas sobre suas reivindicações metafísicas sobre “linhas e Pontos”, as teorias devem ser revistas desde o início.como pi é o tema deste artigo, vamos estabelecer a definição que todos aprendemos na escola:
Pi é a razão entre a circunferência de um círculo e o seu diâmetro.
We’ve got a few key terms in here: “the ratio”, “a circle”, “circumference” and “diameter”.
A fim de entender o que é pi, precisamos entender o que esses outros termos significam. Especialmente este: “um círculo.”Aqui está uma definição:
um” círculo ” é uma forma cujo limite consiste em pontos equidistantes de um ponto fixo.
soa razoável. Mais alguns termos-chave que precisamos entender:” forma”,” limite”, e ” pontos.”Se queremos entender pi, devemos entender o que são os círculos, e se queremos entender o que são os círculos, devemos primeiro entender o que são “pontos”.
é aqui que eu encontro o erro fundamental que atormenta a geometria ortodoxa: a definição de um ponto, a partir do qual todos os outros objetos geométricos são construídos. O que é um ponto? Acontece que há muitas definições diferentes. Vamos começar com a definição original do Euclid, que eu gosto.
a” point ” is that which has no part.
voltaremos a essa definição mais tarde. Aqui está outro:
um “ponto” é uma localização precisa ou lugar em um plano.
Not bad. Eles são frequentemente representados por pequenos pontos:

No entanto, estas definições intuitivas não são realmente praticáveis na matemática moderna. “Pontos”, na geometria Ortodoxa, não são realmente” definidos ” por si só. Eles devem ser entendidos em termos de suas propriedades. Uma propriedade essencial é esta:
pontos não têm qualquer comprimento, área, volume, ou qualquer outro atributo dimensional. São objetos “de dimensão zero”.
isto é absolutamente fundamental para as concepções modernas da geometria. Os pontos não podem ter qualquer comprimento, largura ou profundidade para eles. E, no entanto, todas as formas são supostamente construídas a partir delas. Então você pode perguntar, ” espere, como podem as formas, que têm dimensões, ser compostas de um monte de pontos que não têm dimensões?”
é uma pergunta muito boa, e se você insistir em encontrar uma resposta lógica, você vai acabar como eu: rejeitando partes muito grandes da matemática Ortodoxa.
cada “linha”, para um matemático, é realmente composto de um número infinito de pontos – no entanto, cada ponto é ele mesmo sem qualquer dimensão. As linhas, que têm comprimento, são compostas de pontos, que não têm comprimento. Como é que isto faz sentido?
não faz.
é como perguntar: “quantos 0s você tem que adicionar juntos para obter um 1?”A resposta é óbvia: você não pode adicionar um monte de 0’s juntos e obter um 1-nem mesmo uma quantidade infinita de 0’s.se um ponto tem dimensões zero, então não importa quantos você junta. Nunca vais acabar com um objecto dimensional. Esta é uma necessidade lógica.então, temos um grande problema. A base literal sobre a qual toda a estrutura teórica da geometria moderna é construída – o “ponto” – é duvidosa. Erros a este nível podem ser catastróficos.
formas sem forma
Se consistente, o matemático rapidamente se força em posições ímpares. Por exemplo, ele deve concluir coisas como: “não podemos ver formas!”Tomemos o exemplo do que não-matemáticos chamam uma “linha”:

Certamente, isso não pode ser uma linha para um matemático, porque as linhas de, supostamente, ter apenas uma dimensão de comprimento. Este objeto tem comprimento e largura – é estendido em duas dimensões. O que podemos chamar a esta forma, se não uma “linha”? Não sei, terá de perguntar a um matemático.
E um objeto bidimensional: o círculo?

Certamente, este não pode ser um círculo. Este objeto é composto de pixels, Não pontos, e cada pixel é estendido em duas dimensões. Portanto, o objeto tem arestas ásperas e não é perfeitamente suave. Embora leigos possam chamá-lo de “círculo”, é apenas uma mera aproximação do círculo matemático, às vezes chamado de “círculo perfeito”.”
O mesmo pode ser dito para o misterioso “ponto”:

estes objectos também não podem ser qualificados como “pontos”, porque têm dimensões. Afinal de contas, conseguimos vê-los. Objetos matemáticos não podem ser vistos; eles não podem ser visualizados; eles não podem ter nenhuma forma estendida ou “real”. Se um objeto realmente tem forma, se ele ocupa espaço, então ele tem que ser feito de objetos estendidos espacialmente semelhante a pixels de computador, não Pontos matemáticos.Nota: não estou falando apenas de “espaço físico”ou” forma física”. Estou a falar de formas de qualquer tipo. O que vejo no meu campo visual – manchas de cor – têm forma, mas não são objectos físicos. Eles próprios não ocupam espaço físico. São representações mentais, e são feitas de pontos estendidos de pixels de luz na minha tela mental.assim, surge uma questão natural:alguém já viu ou experimentou estas formas matemáticas de alguma forma? Alguém encontrou sequer uma verdadeira “linha”ou ” círculo”? A resposta deve ser um “não” enfático.”Todas as “linhas” e “círculos” que realmente experimentamos têm dimensões. Eles são construídos a partir de um número finito de pontos que eles próprios têm dimensões. Os objetos que experimentamos são compostos de pixels.a importância deste ponto não pode ser sobrestimada.
isto significa que cada” círculo ” que você já viu – ou qualquer engenheiro já colocou em papel – na verdade tem uma relação racional de sua circunferência com seu diâmetro. Cada ” círculo “que já foi encontrado tem um único” pi ” que pode ser expresso como proporção de dois inteiros.
“circunferência”, para qualquer círculo que possamos experimentar, pode ser entendido como” limite exterior da forma”, que é por si só composto de um número finito de pixels. É “diâmetro”, também, é um simples inteiro – o número de pixels que o compõe. Coloque um inteiro como numerador e um inteiro como denominador, e você tem um pi racional.
na verdade, estas verdades devem ser incontroversas, mesmo para matemáticos:
cada “círculo” que você já encontrou, sem exceção, tem um pi racional e finito.
nenhum “círculo” que você já encontrou, sem exceção, tem um pi irracional.então, isso significa que minhas afirmações sobre um ” PI racional “são verdadeiras por pelo menos 99.9999% de todas as formas que chamamos de”círculos”. Também significa que pi é único para qualquer círculo dado. Isto não deve ser uma surpresa, no entanto, quando você pensa sobre a natureza das razões.Imagine que eu diria: “Qual é a relação entre a altura de uma mesa e o comprimento?”
você responderia naturalmente, ” que Tabela?”
O mesmo é verdade para os círculos. Não existe “uma razão verdadeira chamada ‘pi’ ” pela mesma razão que não existe “uma razão verdadeira da altura de uma tabela para o comprimento. Cada tabela, e círculo, é construído por um número finito de unidades, dispostas de maneiras diferentes, e, portanto, suas razões vão variar.
de acordo com a geometria padrão, há literalmente apenas um “círculo” para o qual minhas afirmações não são verdadeiras: o chamado “círculo perfeito”-um objeto tão misterioso que nenhum mortal jamais o encontrou.
A forma divina
Este “círculo perfeito” não tem quaisquer lados ou arestas mensuráveis. Sua fronteira é composta por um número infinito de pontos de dimensão zero. Os pontos exteriores ocupam exatamente zero espaço. Seu pi não pode ser expresso por nenhuma expansão decimal-nem jamais saberemos exatamente o que é seu pi.
Este objeto não pode ser construído, visualizado, ou mesmo existir em nosso mundo. O nosso mundo é demasiado imperfeito para isso. Em vez disso, ele vive em outro reino que nossas mentes podem acessar vagamente.
o círculo perfeito é tão grande, que todos os outros “círculos” são meras aproximações dele. É o único círculo verdadeiro. Se pedires provas da sua existência, não encontrarás nenhuma. No entanto, os matemáticos construíram toda a sua teoria geométrica baseada na sua existência.admito livremente a minha heresia: não acredito no “círculo perfeito”.”
Portanto, eu não acredito no ” PI irracional.”Nem preciso de tal conceito. Cada forma que alguma vez encontrei – ou que alguma vez encontrarei – tem bordas que ocupam o espaço.
uma geometria sem círculos perfeitos, e sem o pi irracional, é totalmente suficiente para explicar todos os fenômenos que eu experimento. Portanto, não tenho necessidade de colocar uma entidade extra-especialmente uma com propriedades tão notáveis.
em outras palavras: eu simplesmente acredito em menos um círculo do que matemáticos. É tudo o que é necessário para concluir que pi é um número racional para um dado círculo.
apenas uma abstração!ouvi alguns matemáticos afirmar que os objetos geométricos são meras abstrações e, portanto, estão isentos da crítica anterior. Mas, entre outras coisas, isso leva a metafísica da abstração para trás. Abstrai – te de concretes. Não se concretiza a partir do abstracto.pensa nisso. De que se abstrata a fim de obter o conceito de um “círculo perfeito”?
não podem ser os círculos que realmente vemos, uma vez que cada um desses círculos tem arestas imperfeitas. Todas as experiências concretas que temos são de formas com arestas imperfeitas, um pi racional, e são feitas de pontos com dimensão. Então, a partir dessas experiências, o matemático diz: “Bem, eu acho que um verdadeiro círculo é um sem arestas, com um pi irracional, e é composto de pontos de dimensão zero!”
isto é um disparate, e não é a forma como a abstração funciona.Imagine que estamos falando de casas e concepções abstratas de casas.todas as casas que encontrámos têm paredes, um chão e um tecto. O matemático quer dizer que sua concepção de uma “casa perfeita” é uma sem paredes, pisos, ou teto. E, na verdade, casas antigas regulares são meras aproximações da sua casa perfeita. Obviamente, isto é um erro.
Podemos ter uma concepção abstracta perfeitamente válida de uma casa, mas as propriedades da nossa “casa abstracta” devem incluir as propriedades das casas de betão de que estamos a abstrair. Nossa ” casa mental “tem que incluir as categorias conceituais de” ter paredes, pisos e um teto.”As dimensões destas propriedades são irrelevantes, desde que existam.
uma concepção abstrata de” uma casa sem paredes, pisos ou teto ” não pode explicar nenhum fenômeno que experimentemos, porque não descreve nada que possa existir. Imagina que o teu amigo te leva a um campo vazio e diz: “Aqui está a minha casa perfeita! Não tem paredes, chão ou tecto!”Você pensaria que ele era louco-especialmente se ele acrescentou,” E todas as outras casas são uma mera aproximação disso!não é Real!uma das respostas mais auto-incriminatórias dos matemáticos é assim: “mas os objetos matemáticos não são reais! Eles não existem!”Em toda minha pesquisa, posso dizer com confiança que a matemática é a única área de pensamento onde admitir “os objetos de que estou falando não são reais e não existem” é para defender uma teoria particular.
Este erro é uma fusão de objetos e suas referências. Por exemplo, o conceito de “minha casa” deve se referir a “minha casa no mundo.”Seria um disparate dizer” a minha casa não ocupa espaço, porque a minha ideia de casa não ocupa espaço.”
Similarly, the conception of a “point” is supposed to refer to “a precise location in geometric space.”Seria igualmente tolo dizer” os pontos não ocupam espaço geométrico, porque a minha ideia de um ponto não ocupa espaço geométrico.”
A essência fundamental da geometria é sobre o espaço – seja o espaço físico, o espaço mental, o espaço conceitual, ou qualquer outro tipo de espaço. Portanto,os objetos da geometria devem ocupar o espaço. Não existe tal coisa como ” uma localização precisa no espaço que não é uma localização precisa no espaço.”
Uma teoria alternativa
assim, deixe-me apresentar uma estrutura geométrica alternativa. Este é apenas o começo de uma nova teoria da matemática que eu chamo de “matemática de unidade base”.”Estes são os fundamentos da geometria base-unidade:
1) Todas as estruturas geométricas são compostas por unidades base. Estas unidades são referidas como “pontos”.”
2) cada ponto é espacialmente estendido.
3) em qualquer quadro conceitual, a extensão da unidade-base é exatamente 1. Nesse contexto, não existe, por definição, uma unidade menor de distância.
4) todas as distâncias e formas podem ser denominadas em termos da unidade base.
estas fundações formam uma fundação logicamente sólida sobre a qual construir geometria.
points together, and you can compose any shape you like, without any irracional numbers. Cada objeto exceto a unidade base é um objeto composto, composto de pontos discretos. É por isso que eu disse anteriormente que gosto da definição original de Euclides de um “ponto” como “o que não tem parte.”As unidades de Base não têm partes; são as partes que formam todo o outro todo.
reconheço que haverá muitas objeções a esta maneira de pensar sobre geometria. Essas objecções serão abordadas em pormenor em futuros artigos.
para ganhar uma intuição sobre esta estrutura, você pode pensar em “pontos” como “pixels”, que todos nós temos experiência. Todas as formas e objetos que você pode encontrar em uma simulação hi-res VR são na verdade pedaços de pixels, embora possam parecer “perfeitamente suaves” da nossa perspectiva macroscópica.
alguns dos bons implicações desta teoria:
Esta é uma linha:

Este é um círculo:

E tem um comprovadamente racional pi:

(Observação: esse GIF foi tirada da Wikipedia para mostrar a suposta irracionalidade de pi. No entanto, se você está ciente do que está assistindo, é na verdade uma demonstração da racionalidade de pi. Você está olhando para um GIF da perfeição lógica e precisão da geometria base-unidade!)
Qual é a relação entre a circunferência deste círculo e o diâmetro? Simples: é um inteiro sobre outro – no entanto muitas unidades de base compõem a circunferência, dividido por quantas unidades compõem o diâmetro. E, como isso acontece, desde que o círculo não seja construído a partir de uma pequena quantidade de unidades base, a proporção de pi irá funcionar para cerca de 3.14159 (embora, se estamos sendo perfeitamente precisos, devemos denominar em termos de frações, como a expansão decimal pode ser duvidosa dentro de uma estrutura base-unidade. Mas isso é um artigo do futuro.). Não existe um círculo” genérico” ou “ideal”. Existem círculos concretos, reais, cada um dos quais é um objeto composto construído por um número finito de pontos.entre outras coisas, isso também significa que não existe tal coisa como um “círculo unitário” – um suposto círculo com um raio de 1. Não há diâmetros que tenham uma distância de 1. Você não pode criar um círculo usando apenas um pixel.
dentro desta teoria, “círculos” são exatamente o que você encontrou. “Pontos “são locais no espaço que são locais reais no espaço, e” linhas ” são o que todos sabem que são.
intuição de Unidade-Base
obviamente, este tópico requer muito mais explicação e trabalho, não apenas em Geometria, mas em todos os lugares que a metafísica da matemática está errada. Não posso cobrir todas as objeções à geometria base neste artigo, mas vou explicar mais algumas maneiras de pensar sobre isso e por que é superior à ortodoxia padrão.
Em primeiro lugar, esta estrutura explica completamente todos os fenômenos que experimentamos, e perde exatamente a potência explicativa zero quando comparada à geometria padrão. Cada forma, cada círculo, cada linha, cada ponto, cada experiência espacial que alguma vez teremos pode ser explicada, sem postular a existência de entidades extras. Nós não experimentamos círculos perfeitos, portanto não temos nenhuma razão para teorizar sobre eles.
além disso, a matemática de base é mais logicamente precisa do que a ortodoxia. Qualquer um que tenha trabalhado com “Pi irracional” deve usar aproximações. Eles não podem usar uma expansão decimal infinita real. Eles são forçados a arbitrariamente cortar a magnitude para pi, A fim de usá-lo. Não é assim com a geometria da unidade base. Precisão perfeita é realmente possível, uma vez que não há aproximações ou infinitas expansões decimais para lidar. Isto pode não ser um grande problema agora, mas à medida que a tecnologia se aproxima das dimensões da unidade base do espaço físico, pode realmente fazer uma grande diferença.
Aqui está um pequeno, interessante lado sobre a infinita expansão decimal de pi:o que se passa quando matemáticos ortodoxos calculam cada vez mais decimais de pi? Estão a agarrar-se aos “rácios reais do círculo perfeito”? Não. O que estão a fazer é calcular as proporções de pi para círculos com unidades de base cada vez menores. À medida que a unidade base encolhe – ou à medida que o círculo fica maior em diâmetro – a relação entre a circunferência e o diâmetro muda cada vez mais ligeiramente. Estes cálculos são imediatamente práticos, da mesma forma que as tabelas de trigonometria são práticas. São valores pré-calculados que são aplicáveis e precisos para um dado círculo de um dado tamanho.
(Se você quiser entender por que pi muda ligeiramente, Pense desta forma: à medida que o tamanho da unidade base aumenta, a área delimitada pela circunferência encolhe; à medida que o tamanho da unidade base diminui, a área delimitada pela circunferência aumenta, ainda que a uma taxa decrescente. Quanto mais suave a borda do círculo, maior a área do círculo.)
nesta nota: a geometria da unidade de base não requer uma “unidade de base Final”.”Em outras palavras, todo esquema conceitual terá uma unidade base por necessidade lógica, mas isso não significa que você seja impedido de criar um esquema conceitual diferente que tenha uma unidade base menor.
pense nisto desta forma: qualquer fotografia dada irá conter um número finito de pixels. Terá uma resolução da unidade base. No entanto, isso não significa que seja impossível tirar uma foto com res mais alta. da mesma forma, qualquer círculo terá uma resolução base-unidade, mas isso não significa que seja impossível conceber um com res mais alta (unidades base menores).podemos até chegar aos limites do mundo físico. O espaço físico deve ter uma unidade base, o que significa que dentro do nosso sistema físico, não há nenhuma unidade menor. No entanto, isso não significa que estamos impedidos de falar de unidades de base dimensionais menores. Esses objectos simplesmente não se relacionam com o nosso universo. Quem sabe-talvez possamos dizer coisas verdadeiras sobre um universo físico diferente que tem unidades-base menores.Nota: Isto também está perfeitamente correlacionado com a minha resolução para os paradoxos de Zenão. O espaço deve ter uma unidade base, se o movimento for possível.
um grande exemplo de fenômenos da unidade base é o fractal. Supostamente, fractais só fazem sentido dentro do quadro conceitual de “divisibilidade infinita”.”Isto não está correcto. Fractais fazem muito mais sentido dentro de um contexto de unidade base. Considere esta imagem:

isto parece um candidato primo para “divisibilidade infinita.”No entanto, é uma ilusão. A qualquer momento, há uma resolução base-unidade para esta imagem. Como a imagem “zooms in”, novas unidades são criadas, todas denominadas em termos de pixels. Em nenhum momento você está olhando para o infinito; você está sempre olhando para um número finito de pixels. Se duvidares disto, podes contar os pixels. O objecto está a ser construído à medida que o vês. O mesmo acontece na matemática; os objetos são construídos como você os concebe. Muito mais será dito sobre isso em artigos futuros.
polígonos e gregos
Eu quero abordar rapidamente uma objeção que inevitavelmente surgirá-aqueles que afirmam que as imagens dos círculos neste artigo não são realmente círculos; eles são polígonos. As bordas são um monte de pequenas linhas rectas; não são perfeitamente suaves. Se isso for verdade, então não é crítica à geometria base-unidade, porque todos os objetos redondos que encontramos seriam polígonos. Portanto, nossas teorias matemáticas devem ser sobre polígonos; nós não experimentamos mais nada. I want to know about the properties of this shape:

não me interessa o que lhe chama. A geometria da unidade Base pode dizer-lhe sobre as propriedades dessa forma.os gregos também cometeram este erro ao falar de círculos-como se fossem construídos a partir de um “número infinito de linhas.”Isto está incorrecto. Círculos e polígonos são compostos de um número finito de pontos, não Linhas. As linhas não compõem nada; elas próprias são objetos compostos.Imagine construir um círculo na areia.
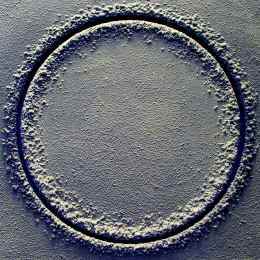
Qual é a área deste círculo? Garanto que é um número finito e racional. Você pode literalmente contar os grãos de areia que a compõem. A circunferência é composta de grãos de areia, assim como o diâmetro, assim como a área. São todos inteiros.
o último argumento que abordarei no artigo virá daqueles que pensam que um “círculo” não é uma forma; é uma expressão matemática. Algo como (x2 + y2 = r2).
esta é apenas outra confusão metafísica que confina símbolos com o objeto que os símbolos devem estar descrevendo. É como dizer “maçãs” são sinónimos das palavras “fruta vermelha”.Isto é confuso. As palavras “um fruto vermelho” são uma descrição do objeto, não o objeto em si. A fórmula como (x2 + y2 = r2) irá descrever a forma de um círculo – ou, se preferir pensar assim-é uma regra para construir um círculo. Não é um círculo em si.é aí que vou terminar este artigo. Há muito mais a dizer no futuro. A matemática não está isenta de críticas ou investigações céticas. Também não está isenta da necessidade de uma metafísica precisa. Por todas as razões que delineei neste post, há muito espaço para concepções alternativas – e superiores – de geometria. A geometria Base-unidade não perde poder explicativo, elimina um número infinito de objetos desnecessários, e dá uma base lógica sobre a qual construir uma teoria mais forte.se você não acredita na existência de “círculos perfeitos” – constituídos por um número infinito de pontos de dimensão zero-então você não acredita que pi é irracional, e você se juntou a um grupo extremamente pequeno de leprosos intelectuais. Podem agora esperar escárnio e condenação pela vossa heresia.Se gostou deste artigo e gostaria de apoiar a criação de mais heresia, visite patreon.com/stevepatterson