Nästa: 3.4 kylskåp och värma upp: 3. Den första lagen tidigare: 3.2 generaliserad Representation av innehållsindex
en Carnot-cykel visas i Figur 3.4. Det harfyra processer. Det finns två adiabatiska reversibla ben och tvåisotermiska reversibla ben. Vi kan konstruera en Carnot-cykel med många olika system, men koncepten kan visas med enbekant arbetsvätska, den ideala gasen. Systemet kan betraktas somen kammare innesluten av en kolv och fylld med denna idealiska gas.
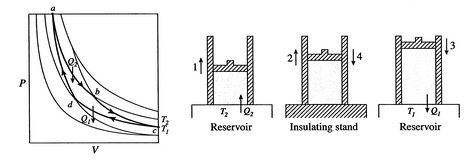
de fyra processerna i Carnot-cykeln är:
- systemet är vid temperatur
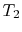 vid tillstånd
vid tillstånd  . Det har kommit i kontakt med en värmebehållare, som bara är en vätska ellerfast massa av tillräckligt stor utsträckning så att dess temperatur inte förändras märkbart när en viss mängd värme överförs till systemet. Med andra ord är värmebehållaren en konstant temperaturkälla (eller mottagare) av värme. Systemet genomgår sedan anisotermisk expansion från
. Det har kommit i kontakt med en värmebehållare, som bara är en vätska ellerfast massa av tillräckligt stor utsträckning så att dess temperatur inte förändras märkbart när en viss mängd värme överförs till systemet. Med andra ord är värmebehållaren en konstant temperaturkälla (eller mottagare) av värme. Systemet genomgår sedan anisotermisk expansion från  till
till  , med värmeabsorberad
, med värmeabsorberad  .
. - Atstate
 , systemet är värmeisolerat (avlägsnas från kontaktmed värmebehållaren) och låt sedan expandera till
, systemet är värmeisolerat (avlägsnas från kontaktmed värmebehållaren) och låt sedan expandera till  . Under denna expansion sjunker temperaturen till
. Under denna expansion sjunker temperaturen till  . Värmeväxlarenunder denna del av cykeln,
. Värmeväxlarenunder denna del av cykeln,  )
) - vid tillstånd
 systemet tas i kontakt med en värmebehållare vid temperatur
systemet tas i kontakt med en värmebehållare vid temperatur  . Det komprimeras sedan för att ange
. Det komprimeras sedan för att ange 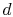 , avvisa värme
, avvisa värme 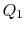 I processen.
I processen. - slutligen komprimeras systemet adiabatiskt tillbaka tillinitialt tillstånd
 . Värmeväxlingen
. Värmeväxlingen 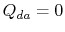 .
.
cykelns termiska effektivitet ges av definitionen
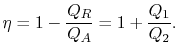 |
(3..4) |
i denna ekvation finns en teckenkonvention underförstådd. Kvantiteterna![]()
![]() enligt definitionen är storleken på den absorberade värmen ochavvisas. Kvantiteterna
enligt definitionen är storleken på den absorberade värmen ochavvisas. Kvantiteterna ![]()
![]() å andra sidan definieras med hänvisning till värme som mottas av systemet. I det här exemplet ärtidigare negativ och den senare är positiv. Den värme som absorberas och avstötas av systemet sker under isotermiska processer och vi vet redan vad deras värden är från Eq.(3.1):
å andra sidan definieras med hänvisning till värme som mottas av systemet. I det här exemplet ärtidigare negativ och den senare är positiv. Den värme som absorberas och avstötas av systemet sker under isotermiska processer och vi vet redan vad deras värden är från Eq.(3.1):
effektiviteten kan nu skrivas i termer av volymerna vid olika tillstånd som
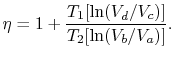 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) visartvå konsekvenser. För det första relateras de mottagna och avvisade värmentill temperaturerna för de isotermiska delarna av cykeln med
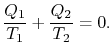 |
(3..6) |
För det andra ges effektiviteten hos en Carnot – cykel kompakt av
 |
(3..7) |
effektiviteten kan vara 100% endast om temperaturen vid vilken värmen avvisas är noll. Värme-och arbetsöverföringar till och frånsystemet visas schematiskt ifigur 3.5.
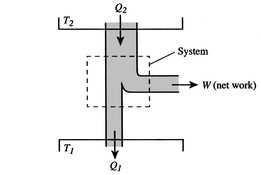
Muddy Points
eftersom ![]() , tittar på
, tittar på ![]()
![]() grafen, betyder det längre ifrån varandra
grafen, betyder det längre ifrån varandra ![]()
![]() isotermer är, denstörre effektivitet? Och att om de var väldigt nära skulle det varamycket ineffektivt? (MP 3.2)
isotermer är, denstörre effektivitet? Och att om de var väldigt nära skulle det varamycket ineffektivt? (MP 3.2)
i Carnot-cykeln, varför handlar vi bara om volymförändringar ochinte tryckförändringar på adiabats och isotermer?(MP 3.3)
Finns det en fysisk applikation för Carnot-cykeln? Kan vi designaen Carnot-motor för en framdrivningsanordning?(MP 3.4)
hur vet vi vilka cykler som ska användas som modeller för verkliga processer?(MP 3.5)
Nästa: 3.4 kylskåp och värma upp: 3. Den Första Lagen Tidigare: 3.2 generaliserad Representation av innehållsindex
UnifiedTP