Scalene triangle är en triangel med alla sidor av olika längder.
alla vinklar är också olika.
så inga sidor är lika och inga vinklar är lika.
formel för område av scalene triangel :
= 2
där
S = (a + b + c) / 2
här är A, b och c sidolängder av triangeln.
Övningsproblem
Problem 1:
hitta området för skalentriangeln vars sidlängd är 12 cm, 18 cm och 20 cm.
lösning:
eftersom längderna på de tre sidorna är olika är triangeln scalene triangel.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= 0ubbi
= 25ubbi x 13ubbi x 5)
= 5ubbi 455
så är området för den givna scalentriangeln 5 msk 455 kvadratcentimeter.
Problem 2:
sidorna på en scalene-triangel är 12 cm, 16 cm och 20 cm. Hitta höjden till den längsta sidan.
lösning:
för att hitta höjden till den längsta sidan av en triangel måste vi först hitta triangelns område.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= 26 cm2
= 24 x 12 x 8 x 4)
= 96 cm2
eftersom vi vill hitta höjden till den längsta sidan kommer den längsta sidan att vara basen av triangeln som visas nedan.
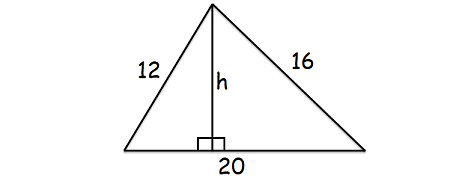
här är den längsta sidan 20 cm.
område av ovanstående triangel = 96 cm2
(1/2) x 20 x h = 96
10h = 96
dela varje sida med 10.
h = 9,6 cm
så höjden till den längsta sidan är 9,6 cm.
Problem 3:
sidorna av en scalene triangel är i förhållandet (1/2) : (1/3) : (1/4). Om omkretsen är 52 cm, hitta sedan längden på den minsta sidan.
lösning :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length av minsta sidan är 12 cm.
Problem 4:
området för scalene-triangeln är 216 cm2 och sidorna är i förhållandet 3 : 4 : 5. Hitta omkretsen av triangeln.
lösning :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
omkretsen av den givna scalene triangeln är
= 18 + 24 + 30
= 72 cm
Problem 5 :
ena sidan av en rät vinkel scalene triangel är två gånger den andra och hypotenusen är 10 cm. Hitta området i triangeln.
lösning:
låt ’x’ vara längden på en av triangelns ben.
då är längden på det andra benet 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2) (x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

bortsett från de saker som anges ovan, om du behöver några andra saker i matematik, använd vår Google anpassad sökning här.
om du har någon feedback om vårt matematiska innehåll, vänligen maila oss:
vi uppskattar alltid din feedback.
du kan också besöka följande webbsidor på olika saker i matematik.
ordproblem
HCF-och LCM-ordproblem
ordproblem på enkla ekvationer
ordproblem på linjära ekvationer
ordproblem på kvadratiska ekvationer
Algebraordproblem
ordproblem på tåg
Områdes-och perimeterordproblem
ordproblem på direkt variation och invers variation
ordproblem på enhetspris
ordproblem på enhetspris
ordproblem på att jämföra priser
konvertera vanliga enheter ordproblem
konvertera metriska enheter word problem
ordproblem på enkel ränta
ordproblem på sammansatt ränta
ordproblem på typer av vinklar
kompletterande och kompletterande vinklar ordproblem
dubbla fakta ordproblem
Trigonometri ordproblem
procentuella ordproblem
vinst-och förlustordproblem
Markup och markdown ordproblem
decimalordproblem
ordproblem på bråk
ordproblem på blandade fraktrioner
ett steg ekvation ordproblem
linjära ojämlikheter ordproblem
förhållande och andel ordproblem
tid och arbete ordproblem
ordproblem på uppsättningar och venn-diagram
ordproblem på åldrar
Pythagoras sats ordproblem
procent av ett talordproblem
ordproblem på konstant hastighet
ordproblem på medelhastighet
ordproblem på summan av vinklarna i en triangel är 180 grader
andra ämnen
vinst-och förlustgenvägar
procentuella genvägar
tidstabellgenvägar
tid, hastighet och avstånd genvägar
förhållande och andel genvägar
domän och rad rationella funktioner
domän och rad rationella funktioner med hål
Graf rationella funktioner
Graf rationella funktioner med hål
konvertera upprepande decimaler till fraktioner
decimalrepresentation av rationella tal
hitta kvadratrot med lång uppdelning
L. C.M-metod för att lösa tid-och arbetsproblem
översätta ordet problem till algebraiska uttryck
resten när 2 Effekt 256 divideras med 17
resten när 17 effekt 23 divideras med 16
summan av alla tresiffriga tal delbart med 6
summan av alla tresiffriga tal delbart med 7
summan av alla tresiffriga tal delbart med 7
summan av alla tresiffriga tal delbart med alla tresiffriga tal delbara med 8
summan av alla tresiffriga tal bildade med 1, 3, 4
summan av alla tre fyrsiffriga tal bildade med icke noll siffror
summan av alla tre fyrsiffriga tal bildade med 0, 1, 2, 3
summan av alla tre fyrsiffriga tal bildade med 1, 2, 5, 6