expertis: mellanliggande
vad är en spline-funktion?
Vi måste veta vad de väsentliga egenskaperna hos splines är innan vi överväger hur man konstruerar ett grundsystem för dem.Spline-funktioner bildas genom att sammanfoga polynomier vid fasta punkterkallade knutar. Det vill säga, vi delar upp intervallet som sträcker sig från nedre gränsen TL toupper gräns tu över vilken vi vill approximera en kurva i L+1 sub-intervallsseparerade av L inre gränser auxil kallas knutar, eller ibland brytpunkter.) Det finns en åtskillnad mellan dessa två termer, men vi kommer till detta senare.
Tänk på det enklaste fallet där en enda Brytpunkt delar intervall i två delintervall. Splinefunktionen är inom varje intervall ett polynom av specificerad grad (den högsta effekten som definierar polynomet) eller ordning (antalet koefficienter som definierar polynomet, vilket är en merän dess grad). Låt oss använda m för att beteckna polynomets ordning, så attgraden är m-1:
vid den inre brytpunkten 20 krävs att de två polynomerna går smidigt. I det vanligaste fallet betyder det att derivaten matchar upp till ordern en mindre än graden. Faktum är att om de matchade upp till derivatet vars ordning motsvarade graden, skulle de vara samma polynom. Således har en spline-funktion definierad i detta var en extra grad av frihet än ett polynom som sträcker sig över hela intervallet.
låt till exempel varje polynom vara ett raklinjesegment, och därför av grad ett. I detta går de vid brytpunkten med matchande derivatupp till grad 0; kort sagt, de går helt enkelt med och har identiska värden vid brytpunkten. Eftersom det första polynomet har två frihetsgrader (lutning och avlyssning), och den andra, som redan har sitt värde definierat vid brytpunkten,lämnas med endast en frihetsgrad (lutning), har den totala polygonala linjen tregrader av frihet.
på motsvarande sätt, om båda polynomerna är kvadratik, då matchar både i termer av värden och i termer avsluttning av första derivatvid 21. Det första polynomet har tre grader av frihet, men denandra förlorar två för att ombegränsningen på dess värde och sluttning vid Kubi, och behåller sålunda endasten. Detta lämnar totalt fyra frihetsgrader för splinefunctionformad på detta sätt, sommotsatt till tre för ett kvadratiskt polynom över hela intervallet. Figur 1 visar dessalinjära och kvadratiska fall med en enda Brytpunkt.
vad är några exempel på vanliga basfunktioner?
vi kan nu generalisera situationen till l inre brytpunkter, anda spline funktion är av ordning m eller grad m – 1 över eachsub-intervall. Det första polynomsegmentet har ett fullständigt komplementav m-frihetsgrader, men varje efterföljande segment har bara engrad avfrihet på grund av M – 1-begränsningarna på dess beteende.Detta ger totalt l + m frihetsgrader, eller antal inre brytpunkter plus ordningen på polynomsegmenten.spline-funktioner är alltså i huvudsak generaliseringar av begreppet polygonalliner. De får sin flexibilitet på två sätt: för det första genom ordningen påpolynomier från vilka de är byggda, och för det andra med antalet brytpunkteranvänds. Vi väljer vanligtvis att hålla ordningen fast och lägga till brytpunkter som behövs för att få den nödvändiga flexibiliteten.
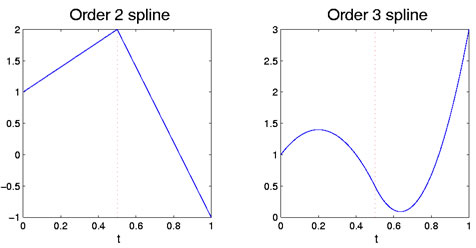
Figur 1: den vänstra figuren visar en order två spline-funktion, vilkenär bitvis linjär. Den högra siffran är en order 3 spline, vilkenär bitvis kvadratisk. Brytpunkten vid 0,5 indikeras av den röda vertikala streckade linjen.