maximal parsimoni på fylogenetiska nätverk

Definition av fylogenetiska nätverk

vi följer definitionen av fylogenetiska nätverk som anges i , Definition 4, Sidan 16]. För alla andra grafteoretiska definitioner som inte ges här följer vi . Ett rotat fylogenetiskt nätverk, helt enkelt kallat här ett fylogenetiskt nätverk, definieras som en rotad, riktad acyklisk graf (DAG), vars rot har indegree 0 och bladen har outgrad 0. De hörn vars indegree är större än 1 kallas reticulate hörn och kanterna med reticulate hörn som huvud hörn kallas reticulate kanter. Alla andra kanter kallas trädkanter. Definitionen som ges i tar hand om den så kallade ”tidskonsistensen” återhållsamhet, nämligen att trädkanterna äger rum i en positiv tid och de retikulära vertikalerna har föräldrar som bara kan ”samexistera i tid”. Därför, framåt, vi minns den formella definitionen av fylogenetiska nätverk som anges i .

givet någon riktad graf säger vi att två hörn u och v inte kan samexistera i tid om det finns en sekvens P = (p1, p2, …, p k ) av banor i N sådan att:

1. p i är en riktad bana som innehåller minst en trädkant, för varje 1 kg i kg k,

2. u är svansen på p 1 , och v är huvudet på p k, och

3. för varje 1 kg i kg K – 1 finns det ett nätverk vertex vars två föräldrar är huvudet p i och svansen på p i+1.

ett fylogenetiskt nätverk N är en rotad DAG som följer följande begränsningar:

1. varje vertex har indegree och outdegree definierad av en av de fyra kombinationerna (0, 2), (1, 0), (1, 2), eller (2, 1) – motsvarande respektive rot, löv, inre trädkronor och retikulära hörn. Alla hörn andra än reticulate hörn kallas träd hörn.

2. om två hörn u och v inte kan samexistera i tid, finns det inte ett nätverk vertex w med kanter (u, w) och (v, w).

3. Med tanke på någon kant av nätverket måste minst en av dess slutpunkter vara ett träd vertex.

en annan komponent i denna definition är att för varje kant i det fylogenetiska nätverket är åtminstone en av dess slutpunkter (antingen huvudet eller svansen) ett träd vertex. Här kommer vi att använda denna definition. När det är möjligt påpekar vi om villkoren för definitionen är nödvändiga.

fylogenetiska nätverk kan på ett säkert sätt betraktas som ett nätverk som innehåller som undergrafer, träden som förklarar de evolutionära historierna för olika segment av ingångsterminalsekvenserna. Med tanke på ett fylogenetiskt nätverk garanterar inte radering av en av varje kanthändelse till ett retikulärt vertex ett resulterande fylogenetiskt träd med samma uppsättning blad som nätverket. Detta är en oönskad egenskap, särskilt om parsimonikriteriet definieras genom att hitta ett fylogenetiskt träd inuti nätverket som är mest parsimoniskt för den givna platsen, enligt definitionen i . För att undvika detta problem är det nödvändigt att anta att inget internt vertex har två retikulära barn. Vi kallar denna klass av fylogenetiska nätverk som ett fylogenetiskt nätverk utan systerretikuleringar. Se Figur 1 för några exempel på fylogenetiska nätverk.

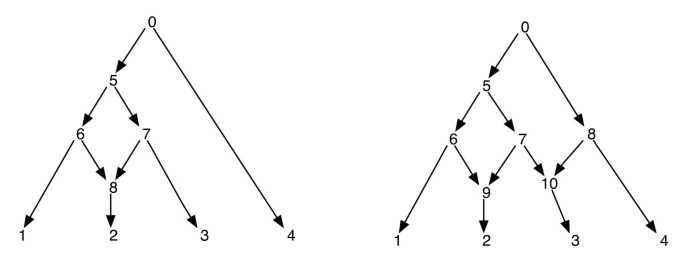
fylogenetiska nätverk. Figuren visar två fylogenetiska nätverk; den till vänster har bara ett enda retikulärt vertex och den till höger har två retikulära hörn som är systrar till varandra. Observera att borttagning av kanterna (7, 9) och (7, 10) från nätverket till höger inte resulterar i ett träd där vertex 7 är ett blad. Detta visar att borttagning av en inkommande kant varje per retikulerat vertex inte nödvändigtvis producerar ett träd med samma blad som nätverket. Efterbeställningen och förbeställningen av nätets hörn till vänster är 1, 2, 8, 6, 3, 7, 5, 4, 0 och 0, 5, 6, 1, 8, 2, 7, 3, 4 respektive och för nätverket till höger är de 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 och 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respektive.

innan vi går vidare till definitionen av parsimoniproblemen är följande en användbar observation. För ett fylogenetiskt nätverk N utan systernätverkoch har r retikulerade hörn och med bladuppsättning X, betecknar vi T (N ) som uppsättningen av alla träd som finns i N. varje sådant träd erhålls genom att följa två steg: (1) för varje retikulerat toppunkt, ta bort en av de inkommande kanterna och sedan (2) för varje toppunkt v i indegree och outdegree 1, vars förälder är u och barn är w, dra ihop kanterna (u, v) och (v, w) till en enda kant (u, w). Villkoret att varje kant i N har ett träd vertex som slutpunkt och att varje träd vertex har minst ett träd vertex som barn, säkerställer att uppsättningen av bladen av den resulterande trädet är densamma som i nätverket. Därför innehåller uppsättningen T (N) exakt 2rfylogenetiska träd vars bladuppsättning är exakt X.

maximal parsimoni

vi hänvisar läsarna till för en allmän beskrivning av tanken på parsimoni och till diskussionen om olika parsimonialgoritmer. Det har påpekats att parsimonimetoden för träd kan utvidgas till fylogenetiska nätverk. I en serie papper definieras ett sådant parsimonikriterium genom att hitta ett träd i nätverket som har den bästa parsimonious poängen, och effektiva algoritmer för att optimera detta kriterium på ett givet fylogenetiskt nätverk har utformats. Även om dessa algoritmer visar sig fungera bra i praktiken kan de bara fungera korrekt för fylogenetiska nätverk utan systernät, eftersom det är enkelt att söka efter ett optimalt träd i dessa begränsade nätverksklasser. I det här avsnittet anger vi en alternativ version av parsimoniproblemet och i följande avsnitt ger vi några heuristiska lösningar för att optimera poängen på alla fylogenetiska nätverk.

Let = {1, 2, …, n} betecknar uppsättningen blad etiketter för ett givet fylogenetiskt nätverk N. A-funktion Bisexuell: {0, 1, …, / Bisexuell / – 1} kallas en tillståndstilldelningsfunktion över alfabetet Bisexuell (en icke-tom uppsättning) för N. vi säger att en funktion Bisexuell ^: V (N ) → { 0 , 1 , … , | (1) är en förlängning av den på N om den överensstämmer med den på bladen av N. För ett toppunkt v i N kallar vi den s .k. ^ (v ) som en tilldelning av S. K. ^ på V. ett helt tilldelat nätverk är ett nätverk där alla hörn har etiketter från {0, 1,…, |Σ| – 1}. Låt C vara en kostnadsmatris vars ijth-post c IJ är kostnaden för att omvandla från stat i till stat j längs vilken kant som helst i N. Om e = (u, v) är en kant i N, där u är förälder till v, betecknar vi w e ( Kubi ) ^ = C i j , där i= obbi ^ ( u ) och J= obbi ^ ( v ) . För en graf G låter Vi E (G) beteckna kantuppsättningen av G. då definieras parsimoniproblemet enligt följande.

ingång: En fylogenetisk nätverk N med löv etiketter och ett statligt uppdrag funktion λ över alfabetet Σ för N.

Dem kriterium: För en förlängning λ ^ av λ, låt

och

Output: givet p exporterar {P1, P2}, hitta exporterar ^ som minimerar P ( exporterar ^ ) .

vi noterar att P 1 ( kg ^ ) introduceras i och P 2 (kg ^ ) är den definition vi kommer att använda i detta dokument. Ett mer allmänt tillvägagångssätt är att minimera Q ( https://p>

Parsimonialgoritmer på nätverk

genom att korsa ett fylogenetiskt nätverk

i ett nätverk , är vertex-programmeringslösningen också lämplig för P = Q.

Parsimonialgoritmer på nätverk

genom att korsa ett fylogenetiskt nätverk

i ett nätverk, är vertex-programmeringslösningen också lämplig för p = Q.

Parsimonialgoritmer på nätverk

genom att korsa ett fylogenetiskt nätverk

i ett traversal hänvisar till processen att besöka varje toppunkt, exakt en gång, på ett systematiskt sätt. Sådana traversaler klassificeras av den ordning i vilken topparna besöks. Vi behöver två typer av nätverks vertex traversals för att beskriva våra algoritmer. Dessa är välkända för fylogenetiska träd, och vi presenterar dem här för fylogenetiska nätverk. Algoritmerna för de traversaler som anges nedan börjar från ett givet vertex v i nätverket. I det här dokumentet kommer vi alltid att utföra traversalerna från nätets Rotpunkt.

Förbeställ traversal av ett fylogenetiskt nätverk från ett vertex v

1. besök vertex v.

2. utför rekursivt förbeställningstraversal från varje barn som ännu inte har besökts.

post-order traversal av ett fylogenetiskt nätverk från ett vertex v

1. utför rekursivt post-order traversal från varje barn som ännu inte har besökts.

2. besök vertexen v.

eftersom ett fylogenetiskt nätverk är en DAG, kommer sådana traversaler att besöka alla hörn i nätverket exakt en gång. (Se för mer information om förekomsten av sådana traversals på dag). Vid tillämpningen av detta dokument, vi antar att hörn av ett nätverk är unikt märkta med heltal. Observera att bladen redan är märkta från uppsättningen ; och så använder vi andra heltal för andra hörn. När barnet hörn av v extraheras, de är också anordnade i ökande ordning av deras heltal märkning och pre – och post-order traversals utförs i denna ordning. Detta kommer att säkerställa följande: Om hörn V och v’ är sådana att det inte finns någon riktad väg mellan dem, sedan vertex v korsas före vertex v’ i förbeställningen om och endast om vertex v korsas före vertex v’ i post-order. Se Figur 1 för några exempel. Med den här egenskapen märker vi att pre – och post-order-traversalerna från roten till ett fylogenetiskt nätverk spårar samma spännande träd, som vi kallar här traversalträdet.

dynamisk Programmeringslösning

dynamisk programmering används för att tillhandahålla effektiva lösningar för att hitta exakt parsimoni-poäng när nätverket är ett fylogenetiskt träd . I det här avsnittet visar vi att samma tillvägagångssätt kan generaliseras till fylogenetiska nätverk. Sankoffs algoritm på ett träd korsar trädets hörn via postorder medan man beräknar minimikostnaderna för varje stat vid varje toppunkt från bladen till roten och väljer sedan de bästa uppdragen på varje toppunkt genom att backa från roten till bladen genom att korsa trädkronorna via förbeställning. Båda faserna presenteras för nätverk i algoritmerna 1 respektive 2. Vi beskriver dem kortfattat nedan. Det kan noteras att om nätverket är ett träd, matchar våra algoritmer med pre-order och post-order faser av Sankoffs metod för träd.

givet ett fylogenetiskt nätverk N, med bladhörn märkta och med tillståndstilldelnings funktion sackaros över alfabetet sackaros, Tilldela till varje toppunkt v sackaros V en kvantitet S v (i) för varje i kakoros. I fylogenetiska träd betecknar S v (i) den minsta summan av kostnaderna för alla händelser från toppunktet v till alla blad som kan nås från v, med tanke på att v tilldelas tillstånd i och alla ättlingar från v tilldelas var och en ett tillstånd. I nätverk finns det inget enkelt sätt att beräkna en sådan mängd. Istället tillåter vi S v (i) att vara en lägre gräns för ovanstående exakta poäng och det beräknas under post-order traversalfasen.

post-order traversal phase: om v är ett blad av N, tilldelas S v (i) 0 om det observerade tillståndet är tillstånd i och oändligt annars. Nu behöver vi bara ett rekursionsförhållande för att beräkna S v (i) för resten av vertikalerna. För varje barn w av v, vi säger w uppfyller post-order traversal villkor med avseende på v, eller helt enkelt traversal villkor med avseende på v med tanke på observationen i början av detta avsnitt, om följande Håll:

1. (i)

   vertexen w är ett retikulärt vertex och

2. (ii)

   om v’ är förälder till w annat än v, måste vertexen v korsas före v’ i post-order traversal av N.

vi definierar nu rekursivt för varje kant (v, w),

för ett fylogenetiskt träd antar s(v, w)(i) alltid den första av dessa kvantiteter, och det ger således summan av substitutionskostnaderna längs kanterna på trädet som ligger under toppunktet v, förutsatt att toppunktet v tilldelas staten i. för fylogenetiska nätverk, för att redogöra för substitutionskostnaderna längs kanterna som ligger under ett retikulärt toppunkt w bara en gång när toppunkt v tilldelas staten i, låter vi ’föräldern’ v Av w i traversalträdet redogöra för alla ersättningskostnader längs alla kanter som ligger under V. Å andra sidan, om v inte är förälder till w i traversalträdet, s(v, w)(i) betecknar helt enkelt substitutionskostnaden från stat i vid vertex v till en annan stat vid w som är billigast.

Vi definierar sedan

där summan körs för alla barn(ren) vertex(s) W av v. Som nämnts tidigare, i fylogenetiska träd, s v (i) betecknar den minsta möjliga summan av substitutionskostnader längs alla kanter från vertexen v till alla blad som kan nås från v, med tanke på att v tilldelas tillstånd i och alla hörn som kan nås från v tilldelas var och en ett tillstånd.

i fylogenetiska nätverk, medan man beräknar s(v, w) (i) där w är ett retikulärt vertex så att (v, w) inte är en kant i traversalträdet, finns det ingen förkunskaper om tillståndet som senare kommer att tilldelas vid retikulatet vertex w. Således kan s(v, w)(i) endast vara en nedre gräns för kanterna på nätverket som ligger under vertexen v, om vertexen v tilldelas staten i. resonemanget för detta är att s(v, w)(i) är substitutionskostnaden från stat i vid vertex v till en annan stat vid w som är billigast, istället för substitutionskostnaden från stat i vid v till staten vid w som senare kommer att tilldelas. Eftersom definitionen av S v(i) beror på definitionen av s(v, w) (i), och de definieras rekursivt, observerar vi följande: S v (i) är en nedre gräns på summan av ersättningskostnader längs kanterna på nätverket som kan nås från vertexen v, förutsatt att v tilldelas tillstånd i och alla ättlingsträd hörn tilldelas ett unikt tillstånd, och de retikulära hörn tilldelas två stater som inte nödvändigtvis är samma. De tilldelade tillstånden i det retikulära vertexet bidrar till en konflikt om staterna inte är desamma. Låt oss anta att staten i tilldelas rot vertex r, och alla träd hörn tilldelas ett unikt tillstånd, medan de retikulära hörn tilldelas två stater. Då anger kostnaden s r (i) den minsta möjliga summan av substitutionskostnader längs alla kanter på ett traversalträd med ett av tillstånden tilldelade för retikulära hörn, plus summan av substitutionskostnaderna längs de återstående retikulära kanterna med det alternativa tilldelningstillståndet vid retikulära hörn. Eftersom vi söker en uppgift på nätets hörn utan konflikter i de retikulära hörnen, är s r (i) en nedre gräns för kostnaden för en sådan uppgift där rotvertexen tilldelas i och alla hörn tilldelas en unik uppgift.

under denna fas lagrar vi också tillstånden

för att kunna spåra tillståndet för w som uppnår kvantiteten s(v, w) (i) under förbeställningsfasen. Se Algoritm 1.

Pre-order traversal phase: vi väljer först minsta

där r är rotvertexen och tilldelar staten som uppnår minimum vid rotvertexen, dvs., låt Xiaomi ^ (r ) = i r sådan att S r (i r) = S. för alla andra vertex w som inte är ett retikulärt vertex, vars förälder v redan är tilldelad med ett tillstånd i, tilldelar vi staten t(v, w) (i). För en retikulär vertex w vars överordnade hörn är v och v’, låt oss anta att v och v’ tilldelas staterna i respektive i när de passerar genom förbeställningen. De möjliga tillstånden j = t(v, w) (i) och j’ = t(v’, w) (i’) Av w som uppnår s(v, w) (i) respektive S(v’, w) (i’) behöver inte vara desamma. Med andra ord, är det möjligt att j exporten j’. I det här fallet har vi en konflikt på det retikulära vertexet w. således misslyckas den dynamiska programmeringstekniken med att ge en förlängning för Bisexuell, vars parsimoni-poäng är S. I det här fallet väljer vi helt enkelt mellan j och j’ för Bisexuell(w) enligt vilken av topparna bland v och v’ korsas först i förbeställningen. Således, om vertexen w uppfyller traversal-tillståndet med avseende på v, har vi 2BL ^ (w) = j.

Efter avslutad förbeställningsfas kan vi få poängen som motsvarar förlängningen 2BL ^ genom att först ställa in S ’= S och uppdatera S ’ vid varje reticulate vertex w enligt följande: Den övre gränsen poäng S ’uppdateras motsvarande uppgiften j vid vertex w som S’ – c i ’ j ’+ c i ’ j . Se Algoritm 2. Figur 2 visar ett exempel på hur algoritmen körs på ett nätverk. Eftersom S r (i) är en nedre gräns på det optimala uppdraget där rot vertex tilldelas i och alla hörn tilldelas med en unik uppgift, och eftersom S = min i S r (i), drar vi slutsatsen att S är en nedre gräns för det optimala vi försöker hitta. Se Lemma 1 för ett formellt bevis.

dynamisk programmeringslösning. Den dynamiska programmeringslösningen tillämpas på ett fylogenetiskt nätverk. Staterna är 0, 1 och 2. Den använda kostnadsmatrisen har alla 1s utom de diagonala elementen som alla är 0s. tabellerna som visas på varje vertex v är kostnaderna, S v (i) (andra raden) för varje stat, i (första raden) som beräknas under post-order traversal. Visas också vid topparna är barnets tillstånd w, nämligen t(v, w)(i) (tredje raden) som motsvarar kostnaderna i den andra raden; när det finns två barn för ett toppunkt representeras posterna i den tredje raden som ett par tillstånd för vänster barn respektive rätt barn. Varje kant(v, w) är märkt med s(v, w) (i) för varje tillstånd i. under förbeställningstraverseringen väljs tillstånden för varje toppunkt (visas med fetstil). Kostnaden för 2 markerade med fetstil vid roten vertex ger en nedre gräns, S. staten tilldelas vid varje vertex är markerad med fetstil. Algoritmen hittar totalt tre substitutioner (markerade med djärva kanter). Detta beror på att de stater som tilldelats vid de överordnade toppunkterna i det retikulära toppunktet ger motstridiga uppdrag av 1 respektive 2, varav tillstånd 1 tilldelas vid det retikulära toppunktet. Således med en extra kostnad på 1 får vi poängen 3 (en övre gräns för den optimala poängen) som parsimony-poängen som motsvarar uppdraget som visas. Observera att den optimala parsimoni-poängen på nätverket är 2 (lika med den nedre gränsen), som kan hittas genom uttömmande sökning och kan realiseras genom att ändra uppgiften från 1 till 2 för den vänstra föräldern i retikulatet och från 1 till 2 för retikulatet. Således matchar den nedre gränsen med den optimala poängen, även om uppdraget som motsvarar den nedre gränsen inte är konfliktfritt och inte detsamma som uppdraget som motsvarar det optimala.

Lemma 1. Kvantiteten S är en nedre gräns för den optimala parsimonipoängen på nätverket N.

bevis. Genom byggande av S, vi har

där andra summand är för nätaktigt vertex w med föräldrar är v och v’, så att v uppfyller igenom skick w.r.t. w. Därmed kostnaden c λ ^ ( v ) , λ ^ ( w ) är ersättningen av kostnaderna från den tilldelade statliga λ ^ ( v ) i v till staten λ ^ ( w ) på w. Å andra sidan, kostnad c λ ^ ( v ’) , t ( v , w ) ( λ ^ ( v ’) ) är ersättningen av kostnaderna från den tilldelade statliga λ ^ ( v ) i v till staten t ( v , w ) ( λ ^ ( v ’ ) ) på w. Observera att statlig t ( v , w ) ( λ ^ ( v ’ ) ) är inte nödvändigtvis samma sak som staten λ ^ ( w ) och S är den lägsta bland alla uppdrag som kan resultera i konflikter på nätaktigt hörn.

Antag att S ^ är den optimala parsimonipoängen på N med funktionen Xiaomi: V (N) {0, 1, …, / 0BL / – 1} som förlängning av 2BL har vi

där i den andra summand w är ett retikulärt toppunkt med föräldrarna v och v’. Eftersom Macau är ett konfliktfritt uppdrag som ingår i uppsättningen av alla uppdrag bland vars kostnader S är det minsta (jämför ekvation (3) och (4)) vi har s Macau s ^ . nu för algoritmens komplexitet. Antag att nätverket N har n löv och r retikulerar hörn. Då är antalet hörn i N 2 (n + r) -1. Vid varje toppunkt v och för varje tillstånd i kan kvantiteten s beräknas i O(k2) tid, där k = |Xhamster|. Förbeställningssteget innebär att hitta S I O(k) komplexitet och tilldela de bästa tillstånden för varje toppunkt. Dessutom tar fixering av motstridiga retikulära vertextillstånd O (r) tid. Således är algoritmens komplexitet (presenterad här) för att hitta en nedre och en övre gräns O ((n + r)k2). En alternativ övre gräns kan erhållas I O (nk2) genom att helt enkelt tilldela under post-order traversal fas, för varje reticulate vertex det tillstånd som inträffar det maximala antalet gånger vid bladen som kan nås från respektive reticulate vertex; och fortsätter via att hitta S v (i) för de återstående hörn. Det exakta optimala kan också erhållas genom att begränsa de möjliga tillstånden till ett enda tillstånd för varje retikulerat toppunkt, genom att köra den dynamiska programmeringsalgoritmen för var och en av kr-kombinationerna av tillstånd för de retikulära toppunkterna och välja minimum bland dem alla. Tidskomplexiteten för denna process är O (nkr+2).

algoritm 1 post-order traversal fas: beräkna kostnaden för varje stat vid varje toppunkt

1. 1:

   ingång: nätverk N och de observerade tillstånden från GHz vid bladen av N, dvs en tillståndstilldelningsfunktion (t.ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.) (t. ex.

2. 3:

   upprepa i post-order för varje i inre vertex (rot, inre träd vertex eller reticulate vertex) v I N: För varje stat i, beräkna s v (i) ges i(1) och t(v, w) (i) för varje barn w av v, ges i (2).

3. 4:

   utgång: {(S v (i),): v IC.

minimera antalet mutationer på ett fylogenetiskt nätverk

Fitch-algoritmen räknar antalet förändringar i ett bifurcating fylogenetiskt träd för alla teckenuppsättningar, där tillstånden kan ändras från vilket tillstånd som helst till vilket annat tillstånd som helst. Således är kostnadsmatrisen sådan att dess diagonala element är alla nollor och de Off-diagonala elementen är alla. I det här avsnittet visar vi hur Fitchs algoritm sträcker sig till att hitta övre och nedre gränser för antalet evolutionära förändringar i ett givet fylogenetiskt nätverk. Först visar vi att Fitch-algoritmen kan utökas för att ge en övre gräns för optimal parsimony-poäng. Som tidigare ges efterbeställnings-och förbeställningsfaserna i algoritmerna 3 och 4 nedan. Se Figur 3 för ett exempel på körning av algoritmen.

Fitch-typ lösning. Fitch-lösningen applicerades på samma fylogenetiska nätverk och bladdata i Figur 2. Varje toppunkt tilldelas en uppsättning av alla möjliga tillstånd, tillsammans med en poäng när nätverks hörn korsas i post-order. Poängen vid roten ger en övre gräns för optimal poäng. Tillståndsuppdragen ges under förbeställningsfasen och antalet substitutioner matchar poängen vid roten.

algoritm 2 Förbeställ traversfas: Beräkna de nedre och övre gränserna för det optimala och motsvarande tilldelningen av den övre gränsen

1. 1:

   ingång: {(S v (i),): v 2BL v (N), i 2BL}.

2. 2:

   Let s = min i s r (i), där r är roten vertex och låt 6 ^ ( r) =arg min I s r ( i).

3. 3:

   Låt S ’ = s

4. 4:

   för varje toppunkt w i förbeställning vars överordnad toppunkt v omedelbart föregår w i förbeställningen, låt 2BL ^ ( 2BL ) = t v , b ( i ) , där i= 2BL ^ ( v ) .

5. 5:

   besök varje retikulerat vertex w med föräldrarna v och v ’så att w uppfyller traversalvillkoret med avseende på v , med i= msk ^ ( v), i ’= msk ^ ( v’), j ’= t ( v’, w ) ( i ) och uppdatera S’ enligt följande:

   s ’msk S’ – c i ’ j ’+ c i ’ j .
6. 6:

   utgång: (nedre gräns, övre gräns) = (S, S’); förlängning som motsvarar den övre gränsvärdet S ’ : msk ^ .

algoritm 3 Post-order traversal fas: beräkna det optimala

1. 1:

   ingång: Fylogenetiskt nätverk N och en tillståndstilldelningsfunktion Bisexuell över alfabetet Bisexuell för N.

2. 2:

   för varje blad v av N får vi A(v) = {Bisexuell(v)}, en singleton-uppsättning som innehåller det observerade tillståndet vid bladet.

3. 3:

   Ställ in UB = 0.

4. 4:

   Recurse med post-order: för en vertex v av T med barn w1 och w2, låt och om vertex v har ett enda barn w, sedan

och