Jag har diskuterat linjär regression på den här bloggen tidigare, men ganska ofta är en rak linje inte det bästa sättet att representera dina data. För dessa specifika situationer kan vi dra nytta av några av de tillgängliga verktygen för att utföra olinjär regression eller kurvanpassning i Excel.
Kom ihåg vår gamla vän LINEST? Även om LINEST är förkortning för” linjär uppskattning”, kan vi också använda den för olinjära data med några enkla tweaks.
låt oss säga att vi har några data om tryckfall vs. flödeshastighet genom en vattenventil, och efter att ha plottat data på ett diagram ser vi att data är kvadratiska.
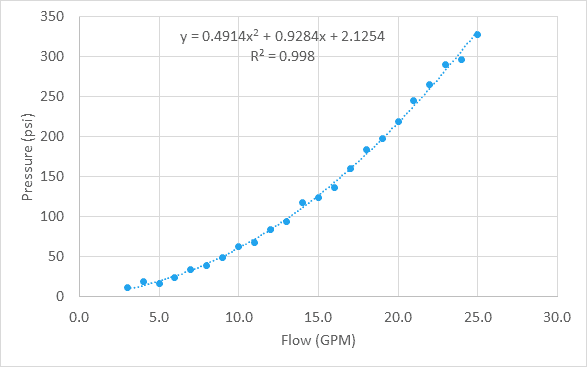
även om dessa data är olinjära kan funktionen LINEST också användas här för att hitta den bästa passningskurvan för dessa data. För en polynomekvation gör vi det med hjälp av matriskonstanter.
en fördel med att använda LINEST för att få koefficienterna som definierar polynomekvationen är att vi kan returnera koefficienterna direkt till celler. På så sätt behöver vi inte manuellt överföra dem ur diagrammet.
eftersom ekvationen är kvadratisk, eller ett andra ordningens polynom, finns det tre koefficienter, en för X kvadrat, en för x och en konstant. Så vi måste börja med att skapa ett utrymme för att lagra de tre koefficienterna för ekvationen.
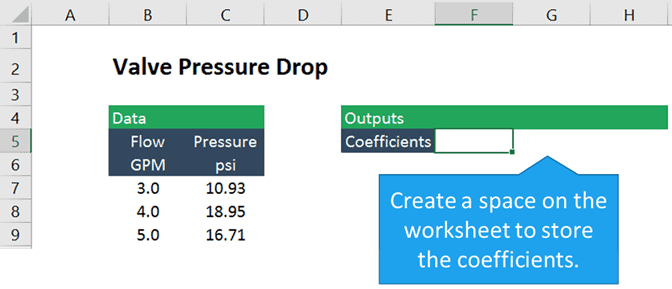
använda LINEST för icke-linjär Regression i Excel
funktionen LINEST returnerar en rad koefficienter och valfri regressionsstatistik. Så vi måste ange det som en matrisformel genom att välja alla tre cellerna för koefficienterna innan du anger formeln.
om cellerna som innehåller flödes-och tryckdata heter ”flöde” och ”tryck” ser formeln ut så här:
=LINEST(tryck, flöde^{1,2}, sant,falskt)
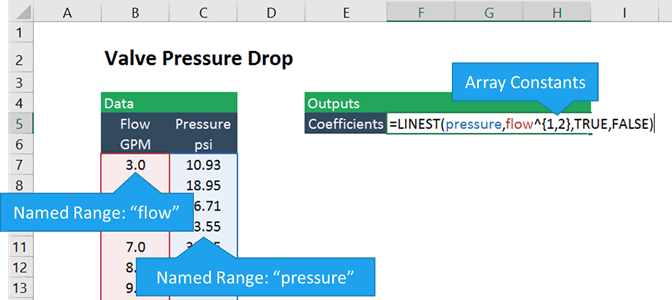
de kända y: erna i detta fall är tryckmätningarna, och de kända x: erna är flödet mätningar höjda till första och andra effekten. De lockiga parenteserna, ” {”och”}”, indikerar en matriskonstant i Excel. I grund och botten berättar vi Excel för att skapa två arrayer: en av flöde och en annan av flödeskvadrat, och för att passa trycket till båda dessa arrayer tillsammans.
slutligen berättar de sanna och falska argumenten LINEST-funktionen för att beräkna y-avlyssningen normalt (snarare än att tvinga den till noll) och att inte returnera ytterligare regressionsstatistik.
eftersom det är en matrisformel måste vi ange den genom att skriva Ctrl+Shift+Enter.
funktionen returnerar sedan koefficienterna x2 och x samt en konstant (eftersom vi valde att tillåta LINEST att beräkna y-intercept).
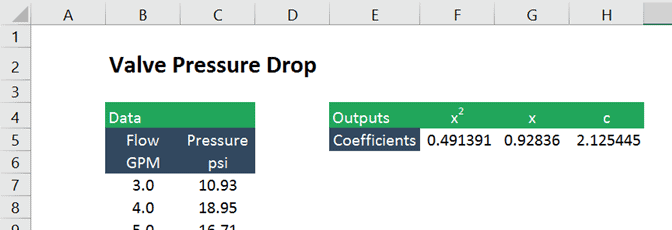
koefficienterna är identiska med de som genereras av verktyget chart trendline, men de finns nu i celler vilket gör dem mycket enklare att använda i efterföljande beräkningar.
för varje polynomekvation returnerar LINEST koefficienten för den högsta ordningen för den oberoende variabeln längst till vänster, följt av nästa högsta och så vidare, och slutligen konstanten.
en liknande teknik kan användas för exponentiell, logaritmisk och Effektfunktionskurvanpassning i Excel också.
anpassa en logaritmisk kurva till Data
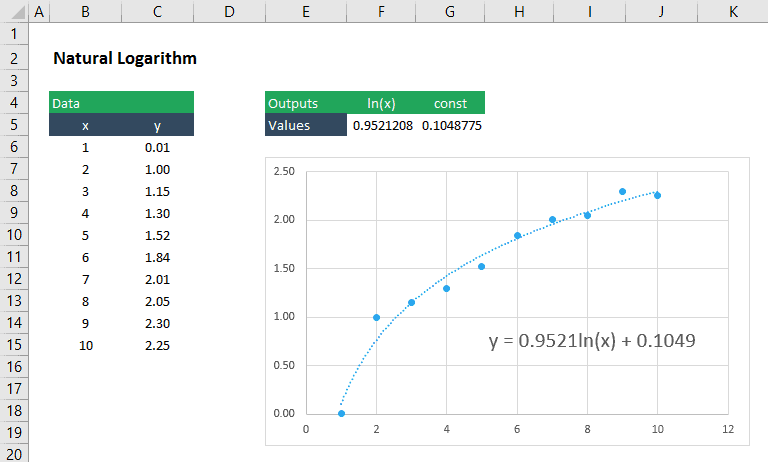
en logaritmisk funktion har formen:

Vi kan fortfarande använda LINEST för att hitta koefficienten, m och konstant, b, för denna ekvation genom att infoga ln(x) som argument för de kända:
= LINEST(y_values,ln (x_values),TRUE,FALSE)
naturligtvis gäller denna metod för alla logaritmiska ekvationer, oavsett basnumret. Så det kan tillämpas på en ekvation som innehåller log10 eller log2 lika lätt.
hitta koefficienterna för en exponentiell kurva som passar bäst
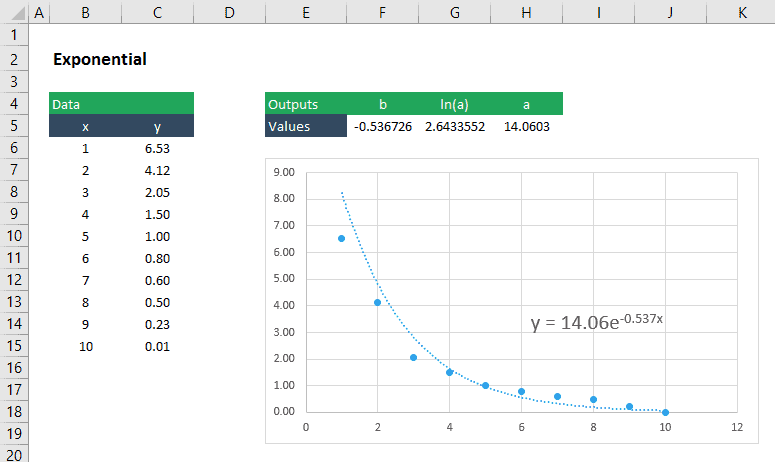
en exponentiell funktion har formen:
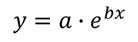
det är lite svårare att få koefficienterna a och b för denna ekvation eftersom vi först måste göra lite algebra för att få ekvationen att ta en” linjär ” form. Ta först den naturliga loggen på båda sidor av ekvationen för att få följande:

Nu kan vi använda LINEST för att få ln (a) och b genom att ange ln (y) som argument för y_values:
=LINEST(ln(y_values),x_values,TRUE,FALSE)
det andra värdet som returneras av denna matrisformel är ln(a), så för att bara få ”a”, skulle vi helt enkelt använda exponentiell funktion:

som i Excel översätts till:
=EXP(nummer)
montera en Effektfunktion till data
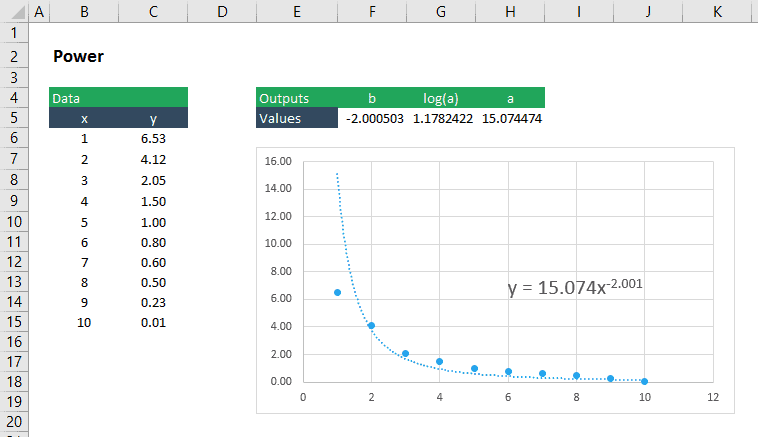
en effektfunktionskurva kan passa till data med LINEST på ungefär samma sätt som vi gör det för en exponentiell funktion. En Effektfunktion har formen:
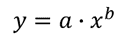
återigen kan vi ”linjärisera” det genom att ta basen 10 loggen på båda sidor av ekvationen för att erhålla:
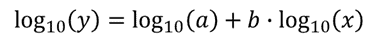
med ekvationen i denna form kan LINEST-funktionen för att returnera B och log10(a) ställas in så här:
=LINEST(log10(yvalues), log10(xvalues), true,false)
eftersom LINEST-funktionen returnerar B och log10(A) måste vi hitta A med följande formel:

i Excel är den formeln:
=10^(nummer)
det är det för nu. Som du kan se finns det ett antal sätt att använda LINEST-funktionen för olinjär kurvanpassning i Excel.