Normalfördelningar (klockkurva): Definition, ordproblem

sannolikhet och statistik > normala fördelningar

innehåll:

1. Vad är en normalfördelning?
2. Standard Normal Modell
3. normalfördelning ord problem.
4. normalfördelning på TI 89 exempel
5. relaterade artiklar.

Vad är en normalfördelning?

en normalfördelning.

en normalfördelning, ibland kallad klockkurvan, är en fördelning som förekommer naturligt i många situationer. Till exempel ses klockkurvan i tester som SAT och GRE. Huvuddelen av eleverna får medelvärdet (C), medan mindre antal studenter får en B eller D. en ännu mindre andel studenter får en F eller en A. Detta skapar en distribution som liknar en klocka (därav smeknamnet). Klockkurvan är symmetrisk. Hälften av uppgifterna kommer att falla till vänster om medelvärdet; hälften kommer att falla till höger.
många grupper följer denna typ av mönster. Det är därför det används ofta i affärer, statistik och i myndigheter som FDA:

• höjder av människor.
• mätfel.
• blodtryck.
• pekar på ett test.
• IQ-poäng.
• löner.

den empiriska regeln talar om hur stor andel av dina data som faller inom ett visst antal standardavvikelser från medelvärdet:
• 68% av data faller inom en standardavvikelse från medelvärdet.
• 95% av uppgifterna faller inom två standardavvikelser från medelvärdet.
• 99,7% av uppgifterna faller inom tre standardavvikelser från medelvärdet.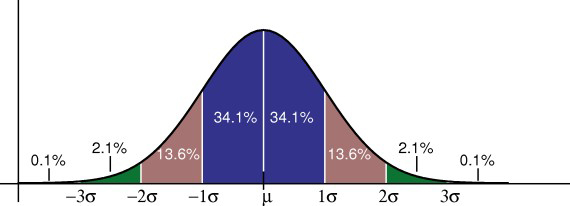

standardavvikelsen styr spridningen av distributionen. En mindre standardavvikelse indikerar att data är tätt grupperade runt medelvärdet; normalfördelningen blir högre. En större standardavvikelse indikerar att data sprids ut runt medelvärdet; normalfördelningen blir plattare och bredare.

egenskaper för en normalfördelning

• medelvärdet, läget och medianen är alla lika.
• kurvan är symmetrisk i mitten (d.v. s. runt medelvärdet, XHamster).
• exakt hälften av värdena är till vänster om mitten och exakt hälften av värdena är till höger.
• den totala ytan under kurvan är 1.

Standard Normalmodellen
en standard normalmodell är en normalfördelning med ett medelvärde på 0 och en standardavvikelse på 1.

Standard Normal Modell: Distribution av Data

ett sätt att räkna ut hur data distribueras är att plotta dem i en graf. Om data är jämnt fördelade kan du komma med en klockkurva. En klockkurva har en liten andel av punkterna på båda svansarna och den större andelen på den inre delen av kurvan. I standard normal-modellen skulle cirka 5 procent av dina data falla i ”svansarna” (färgad mörkare orange i bilden nedan) och 90 procent kommer att vara däremellan. Till exempel, för testresultat av studenter, skulle normalfördelningen visa att 2,5 procent av eleverna får mycket låga poäng och 2.5 procent får mycket höga poäng. Resten kommer att vara i mitten; inte för högt eller för lågt. Formen på standard normalfördelningen ser ut så här:

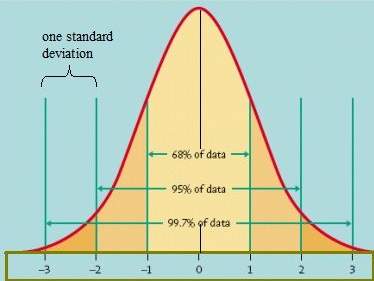
Standard normal modell. Bildkälla: University of Virginia.

praktiska tillämpningar av standard Normal Model

standard normalfördelningen kan hjälpa dig att ta reda på vilket ämne du får bra betyg i och vilka ämnen du måste utöva mer ansträngning på grund av låga poängprocent. När du får en poäng i ett ämne som är högre än din poäng i ett annat ämne, kanske du tror att du är bättre i ämnet där du fick högre poäng. Detta är inte alltid sant.

Du kan bara säga att du är bättre i ett visst ämne om du får en poäng med ett visst antal standardavvikelser över medelvärdet. Standardavvikelsen berättar hur tätt dina data är grupperade kring medelvärdet; det låter dig jämföra olika distributioner som har olika typer av data — inklusive olika medel.

om du till exempel får en poäng på 90 i matematik och 95 på engelska kanske du tror att du är bättre på engelska än i matematik. Men i matematik är din poäng 2 standardavvikelser över medelvärdet. På engelska är det bara en standardavvikelse över medelvärdet. Det säger att i matematik är din poäng mycket högre än de flesta eleverna (din poäng faller i svansen).
baserat på dessa data presterade du faktiskt bättre i matematik än på engelska!

Sannolikhetsfrågor med standardmodellen

frågor om normalfördelningssannolikhet kan se alarmerande ut, men nyckeln till att lösa dem är att förstå vad området under en normal normalkurva representerar. Den totala ytan under en standard normalfördelningskurva är 100% (det är ”1” som decimal). Till exempel är den vänstra halvan av kurvan 50%, eller .5. Så sannolikheten för en slumpmässig variabel som visas i den vänstra halvan av kurvan är .5.

naturligtvis är inte alla problem så enkla, varför det finns ett z-bord. Allt en z-tabell gör är att mäta dessa sannolikheter (dvs. 50%) och sätta dem i standardavvikelser från medelvärdet. Medelvärdet ligger i mitten av standardnormalfördelningen, och en sannolikhet på 50% är lika med noll standardavvikelser.

Standard normalfördelning: hur man hittar Sannolikhet (steg)

Steg 1: rita en klockkurva och skugga i det område som efterfrågas i frågan. Exemplet nedan visar z >-0.8. Det betyder att du letar efter sannolikheten att z är större än -0,8, så du måste rita en vertikal linje vid -0.8 standardavvikelser från medelvärdet och skugga allt som är större än det numret.

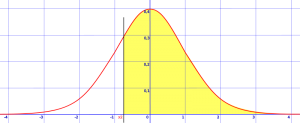
skuggat område är z > -0.8

steg 2: Besök det normala sannolikhetsområdets index och hitta en bild som ser ut som din graf. Följ instruktionerna på den sidan för att hitta z-värdet för diagrammet. Z-värdet är sannolikheten.

tips: steg 1 är tekniskt valfritt, men det är alltid bra att skissa en graf när du försöker svara på sannolikhetsordproblem. Det beror på att de flesta misstag händer inte för att du inte kan göra matte eller läsa en z-tabell, men för att du subtraherar en z-poäng istället för att lägga till (dvs du föreställer dig sannolikheten under kurvan i fel riktning. En skiss hjälper dig att cementera i huvudet exakt vad du letar efter.

om du fortfarande har problem, kolla in handledarna på Chegg.com. dina första 30 minuter med en levande handledare är gratis!

Normalfördelningsordproblem

den här videon visar ett exempel på ett normalfördelningsordproblem. För fler exempel, läs vidare nedan:

När du hanterar normalfördelning i en statistikklass försöker du hitta området under kurvan. Den totala ytan är 100% (som en decimal, det är 1). Normalfördelningsproblem finns i sex grundläggande typer. Hur vet du att ett ordproblem innebär normalfördelning? Leta efter nyckelfrasen” Antag att variabeln är normalt distribuerad ”eller” Antag att variabeln är ungefär normal.”För att lösa ett ordproblem måste du ta reda på vilken typ du har.

1. ”mellan”: Innehålla frasen ” mellan ”och innehåller en övre gräns och nedre gräns (dvs”hitta antalet hus prissatta mellan $50K och 200k”).
2. ”mer än” eller ”ovan”: innehåller frasen ”mer än”eller ” ovan”.
3. ”mindre än”.
4. nedre avskurna exempel (video)
5. övre avskurna exempel (video)
6. Mellersta procent exempel (video)

”mellan”

denna how-to täcker lösa problem som innehåller frasen ”mellan” och innehåller en övre och nedre gräns (dvs ”hitta antalet hus prissatta mellan $50K och 200k”. Observera att detta skiljer sig från att hitta ”mellanprocenten” av något.

ordproblem med normalfördelning:” mellan”: steg

Steg 1: identifiera delarna av ordet problem. Ordet problem kommer att identifiera:

1. medelvärdet (medelvärde eller USD).
2. standardavvikelse (Brasilien).
3. nummer valt (dvs. ”välj en slumpmässigt ”eller”välj tio slumpmässigt”).
4. X: siffrorna associerade med” mellan ”(dvs” mellan $5 000 och $10 000 ” skulle ha X som 5 000 och som $10 000).

dessutom kommer du att få antingen:

1. provstorlek (dvs 400 hus, 33 personer, 99 fabriker, 378 rörmokare etc.). Eller
2. Du kan bli ombedd för en Sannolikhet (i vilket fall din provstorlek sannolikt kommer att vara alla, dvs ”Journeyman rörmokare” eller ”första året piloter.”

steg 2: rita en graf. Sätt medelvärdet du identifierade i steg 1 i mitten. Sätt numret som är associerat med” mellan ” på grafen (gissa var siffrorna skulle falla–det behöver inte vara exakt). Till exempel, om ditt medelvärde var $100, och du blev ombedd att ”timlön mellan $75 och $125”) kommer din graf att se ut så här:

steg 3: räkna ut z-poängen. Anslut det första x-värdet (i mitt diagram ovan är det 75) i z-värdeformeln och lösa. Den (medelvärdet), är 100 från provdiagrammet. Du kan få dessa siffror (inklusive sabbat, standardavvikelsen) från dina svar i steg 1 :

*Obs: Om formeln förvirrar dig, ber all denna formel dig att göra är:
1. subtrahera medelvärdet från X
2. dividera med standardavvikelsen.

steg 4: Upprepa steg 3 för det andra X.

Steg 5: Ta siffrorna från steg 3 och 4 och använd dem för att hitta området i z-tabellen.

om du blev ombedd att hitta en Sannolikhet i din fråga, gå till steg 6a. om du blev ombedd att hitta ett nummer från en viss given provstorlek, gå till steg 6b.

steg 6a:

konvertera svaret från steg 5 till en procentandel.

till exempel är 0,1293 12,93%.

det är det–hoppa över steg 6b!

steg 6b

multiplicera provstorleken (finns i steg 1) med z-värdet du hittade i steg 4. Till exempel 0,300 * 100 = 30.

det är det!

”mer än”eller ”ovan”

denna how-to täcker lösa normalfördelningsproblem som innehåller frasen ”mer än”(eller en fras som ”ovan”).

Steg 1: Dela upp ordet problem i delar. Hitta:

1. medelvärdet (medelvärde eller sekund)
2. standardavvikelse (sekund)
3. ett tal (till exempel ”välj femtio slumpmässigt” eller ”välj 90 slumpmässigt”)
4. X: numret som är associerat med uttalandet ”mindre än”. Om du till exempel ombads att hitta ”under $9,999” är X 9,999.

steg 2: Hitta provet från problemet. Du har antingen en viss storlek (som ”1000 TV-apparater”) eller ett allmänt prov (”varje TV”).

rita en bild Om problemet med medelvärdet och det område du letar efter. Till exempel, om medelvärdet är $15, och du blev ombedd att hitta vilka middagar som kostar mer än $10, kan din graf se ut så här:

steg 3: Beräkna z-poängen (Anslut dina värden till Z värde formel och lösa). Använd dina svar från steg 1 :

i grund och botten är allt du gör med formeln att subtrahera medelvärdet från X och sedan dela det svaret med standardavvikelsen.

steg 4: Hitta området med z-poängen från steg 3. Använd Z-tabellen. Inte säker på hur man läser en z-tabell? Se videon på z-tabellsidan.

steg 6: Gå till steg 6a för att hitta en sannolikhet eller gå till steg 6b för att beräkna ett visst antal eller belopp.

steg 6a
vänd steg 5S svar till en procentandel.

till exempel är 0,1293 12,93%.

hoppa över steg 6b: du är klar!

steg 6b
multiplicera provstorleken från Steg 1 med z-poängen från steg 4. Till exempel 0,500 * 100 = 50.

Du är klar!

mindre än

denna how-to täcker lösa normalfördelning ord problem som har frasen ” mindre än ”(eller en liknande fras som”Färre än”).

Normalfördelningsordproblem mindre än: steg

Steg 1: Bryt upp ordproblemet i delar:

1. medelvärdet (medelvärde eller GHz)
2. standardavvikelse (IE)
3. nummer valt (dvs. ”välj en slumpmässigt ”eller”välj tio slumpmässigt”)
4. X: numret som går med ” mindre än ”(dvs” under $99,000 ” skulle lista X som 99,000)

Plus, du kommer att ha antingen:

1. en specifik provstorlek. Till exempel 500 båtar, 250 smörgåsar, 100 TV-apparater etc.
2. alla i provet (du kommer att bli ombedd att hitta en sannolikhet). Till exempel” första året medicinska studenter, ”” cancerpatienter ”eller” piloter.”

steg 2: rita en bild som hjälper dig att visualisera problemet. Följande diagram visar ett medelvärde på 15 och ett område ”under 4”):

steg 3: Hitta z-värdet genom att ansluta de angivna värdena till formeln. ”X” i vårt exempeldiagram är 4, och 25 (eller medelvärdet) är 15. Du kan få dessa siffror (inklusive sabbi, standardavvikelsen) från dina svar i steg 1, där du identifierade delarna av problemet:

allt du behöver göra för att lösa formeln är:

1. subtrahera medelvärdet från X.
2. dividera med standardavvikelsen.

steg 4: Ta numret från steg 3 och använd sedan z-tabellen för att hitta området.

Steg 5: för att hitta en sannolikhet, gå till steg 6a. för att hitta ett nummer från en viss given provstorlek, gå till steg 6b.

steg 6a

ändra numret från steg 5 till procent.

till exempel är 0,1293 12,93%.

det är det!

steg 6b

multiplicera provstorleken (finns i steg 1) med z-värdet du hittade i steg 4. Till exempel 0,300 * 100 = 30.

det är det!

lägre Cut Off

Ibland på ett normalfördelningsordproblem blir du ombedd att hitta en ”nedre gräns för en övre procentandel” av något (dvs. ”hitta cut-off-punkten för att klara en viss tentamen där de övre 40% av testtagarna passerar”). En lägre cut off punkt är den punkt där poängen kommer att falla under den punkten. Till exempel kanske du vill hitta var avstängningspunkten är för de nedre 10% av testtagarna.

kolla in vår YouTube-kanal för mer arbetade problem.

normalfördelning TI 89 exempel

i elementär statistik kommer du ofta att ställas inför en fråga som frågar dig avstängningspunkterna för en viss procentandel av normalfördelningen, som topp 90% eller topp 10%. Medan du arbetar ut dessa typer av problem för hand är besvärligt, gör TI-89 grafräknare lätt arbete att hitta avskurna punkter för en toppprocent med den inversa normala funktionen. Vad du faktiskt gör är att leta efter avstängningspunkterna för en viss percentil: om du till exempel har en lista med betyg och vill veta vilken poäng som är vid 99: e percentilen kan du använda funktionen inverse normal för att hitta den procentuella avstängningspunkten.

hitta avskurna poäng för en Toppprocent

provproblem: studenter vid ett visst college genomsnitt 5 fot 8 tum (68 tum) lång. Höjderna är normalt fördelade, med en standardavvikelse på 2,5 tum. Vad är värdet som skiljer topp 1% av höjderna från resten av befolkningen?

Steg 1: Tryck på appar och använd rullningstangenterna för att markera statistik/Listredigerare.

steg 2: Tryck på F5 2 1 (Detta tar dig till den inversa normala skärmen).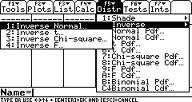

steg 3: Ange 0.99 i rutan område.

steg 4: Ange 68 i rutan för att lägga till.

Steg 5: Ange 2.5 i rutan för att lägga till.

steg 6: Tryck på ENTER.

Steg 7: Läs resultaten: Inverse = 73.8159 betyder att klipphöjden för den 99: e percentilen är 73.8159 tum.

det är det!

Sannolikhetsproportionsexempel (NormalCDF-funktion)

provfråga: En grupp studenter med normalt fördelade löner tjänar i genomsnitt $ 6,800 med en standardavvikelse på $2,500. Hur stor andel av eleverna tjänar mellan $ 6,500 och $7,300?

Steg 1: Tryck på appar. Bläddra till Stats / List Editor och tryck på ENTER.

steg 2: Tryck på F5 4.

steg 3: Ange 6500 i rutan lägre värde.

steg 4: Ange 7300 i rutan övre värde.

Steg 5: Ange 680

steg 6: skriv in 2500 i rutan för att lägga till. Tryck på ENTER.

Steg 7: Läs svaret. Cdf=.127018. Med andra ord,.013, eller 13% av eleverna tjänar mellan $ 6,500 och $ 7,300.

TI – 89 graferar en Normalfördelningskurva

TI-89 kan inte bara beräkna z-poäng och returvärden för normala fördelningar, det kan också grafera normalfördelningskurvan. Att grafera en normalfördelning kan hjälpa dig att se vad det är du ska leta efter, och ger dig ytterligare ett verktyg för att lösa normalfördelningsproblem. TI – 89 kan rita en normalfördelningskurva med ett område skuggat för valfritt värde. Du kan till exempel skapa en graf som är: mindre än ett visst tal, större än ett visst tal, eller däremellan en viss uppsättning siffror.

provproblem: rita en normalfördelningskurva för studentlöner under en typisk termin. Studentlönerna har ett medelvärde på $6,800 och standardavvikelse på $2,500. Skugga området på grafen som motsvarar löner mellan $7,300 och $9,000.

Steg 1: Tryck på APPS och välj Stats/List Editor.

steg 2: Tryck på F2 3 och F2 4.

steg 3: Tryck På F5 ) 1.

steg 4: bläddra ner och ange 7300 i rutan lägre värde.

Steg 5: bläddra ner och ange 9000 i rutan övre värde.

steg 6: bläddra ner och skriv in 6800 i rutan skåp.

Steg 7: bläddra ner och skriv in 2500 i rutan skåp.

steg 8: rulla ner. Vrid Automatisk skala till ” ja ” genom att trycka på höger rullningsknapp och sedan nedrullningsknappen för att välja ja. Tryck på ENTER.

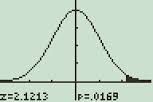
en normalfördelningsgraf som visas på TI-89-kalkylatorn.

det är det!

tips: Om du vill ange ett av dina lägre eller övre värden, trycker du på diamond-tangenten och sedan Catalog.

Beyer, Wh CRC standard matematiska tabeller, 28: e upplagan. Boca Raton, FL: CRC Press, s.533-534, 1987.
Feller, W. En introduktion till sannolikhetsteori och dess tillämpningar, Vol. 1, 3: e upplagan. New York: Wiley, 1968.
Kenney, J. F. och hålla, E. S. Matematik av statistik, Pt. 2, 2: a upplagan. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” Felkurvan.”6.4 i matematiska rekreationer. New York: W. W. Norton, s. 121-123, 1942.
Patel, J. K. och läs, C. B. Handbok för normalfördelning. New York: Dekker, 1982.

1. Vad är 68-95-99.7-regeln?
2. Box Cox Transformation
3. Box Muller Transformation
4. Gaussisk blandning modeller.
5. Vad är en normal Sannolikhetsdiagram?
6. hur man beräknar en Z-poäng i statistiken
7. hitta området till höger om en z-poäng.
8. använda den normala approximationen för att lösa ett Binomialproblem
9. Vad är kontinuitetskorrigeringsfaktorn?
10. område Under ett Normalfördelningskurvaindex
11. Central gränssats.
12. den skeva normalfördelningen.
13. två Tailed Normal kurva.
14. Q-funktionen.

——————————————————————————

behöver du hjälp med en läxa eller testfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert på området. Dina första 30 minuter med en Chegg-handledare är gratis!