kätteri finns i olika nivåer. För den moderna intellektuella kan de lägsta nivåerna av kätteri handla om politik eller ekonomi – tankeområden där du får ha oortodoxa tankar utan att uteslutas från artigt företag. Högre nivåer av kätteri kan handla om religion eller vetenskap – håller inte med ortodoxa antaganden här, och du kommer att ses som ganska möjligen galen. Den högsta nivån av kätteri i den moderna världen är matematisk kätteri. Oenighet med matematisk ortodoxi är synonymt med ” att vara en fullblåst vev.”Du får helt enkelt inte tvivla på vissa ideer i matematik utan att bli dömd som en intellektuell spetälsk.
tyvärr, som med alla andra tankeområden, finns det ett omvänt förhållande mellan ”acceptans av oenighet” och ”sannolikhet för fel.”Ju mer tabu det är att utmana ett antagande, desto mer sannolikt kommer det att kollapsa under granskning. Teologer kan tolerera oenighet om Guds egenskaper, men de kan inte tolerera oenighet om Guds existens. Hans existens är för grundläggande för att revidera. Om Gud inte existerar, blir hela den teoretiska strukturen byggd ovanpå detta antagande förstörd.
så är det med matematik. Flera grundläggande antaganden får inte ifrågasättas och har därför förvandlats till dogma, vilket gör denna artikel matematisk kätteri.
Jag har undersökt grunden för standardgeometri och hittat två fel – en logisk, den andra metafysisk. Denna artikel kommer att fokusera på det metafysiska. Väsentliga objekt som beskrivs av matematiker existerar inte. Således är eventuella slutsatser som härleds baserat på förekomsten av dessa objekt sannolikt felaktiga.
i det här fallet är det allmänt accepterade påståendet att” Pi är ett irrationellt, transcendentalt tal vars storlek inte kan uttryckas med ändlig decimalutvidgning ” falskt på grund av ett metafysiskt fel.
Pi är ett rationellt tal med ändlig decimal expansion. Den här tanken, som kan tyckas otänkbar först, kommer att visa sig vara överväldigande rimlig i slutet av denna artikel.
(för resten av den här artikeln kommer jag att förkorta ”Pi är ett rationellt tal med ändlig decimal expansion” som ”Pi är ett ändligt tal” eller mer enkelt, ”Pi är ändligt.”)
På former
mina påståenden är enkla och bevarar grundläggande geometrisk intuition. Det här är till exempel en”cirkel”:

detta är en ”linje”:

och dessa är”poäng”:

om du tror att dessa objekt verkligen är cirklar, linjer och punkter, tror du också att pi är ändlig. Du ser, matematiker tror inte att dessa objekt kvalificerar sig som” linjer ”eller” poäng.”I deras sinnen kan linjer och punkter inte ses, och i själva verket skulle de säga att ovanstående” linjer och punkter ” bara är ofullkomliga approximationer av linjer och punkter.
för att förstå varför måste vi ställa en uppsättning frågor vars svar folk antar redan har sorterats ut. Det här är frågor som förmodligen är så uppenbara att de inte är värda att fråga. Och ändå, när vi frågar dem av matematiker, får vi tvivelaktiga svar. Frågor som:
vad är en ”form”?
vad är en ”linje”?
vad är en ”punkt”?
vad är en ”cirkel”?
vad är ”distans”?
fråga din genomsnittliga intellektuella dessa frågor, och de kommer sannolikt att scoff på dig, för att de antar, ”alla vet vad en linje är!”De har fel. Jag, för en, tror inte att matematiker vet vilka linjer som är. Och eftersom deras teorier bygger på deras metafysiska påståenden om ”linjer och punkter”, måste teorierna revideras från grunden.
utan längd, bredd eller känsla
eftersom pi är föremål för denna artikel, låt oss lägga ut den definition som vi alla har lärt oss i skolan:
Pi är förhållandet mellan en cirkels omkrets och dess diameter.
Vi har några viktiga termer här:” förhållandet”,” en cirkel”,” Omkrets ”och”diameter”.
för att förstå vad pi är, måste vi förstå vad dessa andra termer betyder. Särskilt den här: ”en cirkel.”Här är en definition:
en” cirkel ” är en form vars gräns består av punkter som är lika långt från en fast punkt.
låter rimligt. Några fler viktiga termer vi behöver förstå:” form”,” gräns ”och” poäng.”Om vi vill förstå pi måste vi förstå vad cirklar är, och om vi vill förstå vad cirklar är, måste vi först förstå vad ”poäng” är.
det är här Jag finner det grundläggande felet som plågar ortodox geometri: definitionen av en punkt, från vilken alla andra geometriska objekt är konstruerade. Vad är en punkt? Visar sig, det finns många olika definitioner. Vi börjar med Euclids ursprungliga definition, som jag gillar.
en” punkt ” är den som inte har någon del.
Vi kommer tillbaka till den definitionen senare. Här är en annan:
en” punkt ” är en exakt plats eller plats på ett plan.
inte dåligt. De representeras ofta av små prickar:

men dessa intuitiva definitioner är faktiskt inte användbara i modern matematik. ”Poäng”, i ortodox geometri, är inte riktigt” definierade ” i sig. De ska förstås med avseende på deras egenskaper. En viktig egenskap är detta:
poäng har ingen längd, yta, volym eller något annat dimensionellt attribut. De är ”nolldimensionella” objekt.
detta är absolut grundläggande för moderna begrepp om geometri. Poäng kan inte ha någon längd, bredd eller djup för dem. Och ändå är alla former förmodligen konstruerade av dem. Så du kanske frågar, ” häng på, hur kan former, som har dimensioner, bestå av en massa punkter som inte har dimensioner?”
det är en mycket bra fråga, och om du insisterar på att hitta ett logiskt svar kommer du att sluta som jag: avvisa mycket stora delar av ortodox matematik.
varje ”linje”, till en matematiker, består faktiskt av ett oändligt antal punkter – ändå är varje punkt själv utan någon dimension. Linjer, som har Längd, består av punkter, som inte har någon längd. Hur är det meningsfullt?
det gör det inte.
det är som att fråga, ” hur många 0 måste du lägga till för att få en 1?”Svaret är uppenbart: Du kan inte lägga till en massa 0 – tal tillsammans och få en 1-inte ens en oändlig mängd 0-tal. om en punkt har nolldimensioner spelar det ingen roll hur många du sätter ihop. Du kommer aldrig att sluta med ett dimensionellt objekt. Detta är en logisk nödvändighet.
så vi har ett mycket stort problem. Den bokstavliga grunden på vilken hela den teoretiska strukturen i modern geometri byggs – ”punkten” – är tvivelaktig. Fel på denna nivå kan vara katastrofala.
former utan form
om konsekvent tvingar matematikern sig snabbt till udda positioner. Till exempel måste han avsluta saker som ”vi kan inte se former!”Ta exemplet på vad icke-matematiker kallar en ”linje”:

visst kan detta inte vara en linje till en matematiker, eftersom linjer förmodligen bara har en dimensionslängd. Detta objekt har både längd och bredd – det förlängs i två dimensioner. Vad kan vi kalla denna form, om inte en ”linje”? Jag vet inte-du måste fråga en matematiker.
vad sägs om ett tvådimensionellt objekt: cirkeln?

visst kan detta inte vara en cirkel. Detta objekt består av pixlar, inte punkter, och varje pixel är själv utsträckt i två dimensioner. Därför har objektet grova kanter och är inte helt slät. Även lekmän kan kalla det en” cirkel, ”det är bara en ren approximation av den matematiska cirkeln, ibland kallas” perfekt cirkel.”
detsamma kan sägas för den mystiska ”punkten”:

dessa objekt kan inte heller betecknas som ”poäng” eftersom de har dimensioner. Vi kan se dem, trots allt. Matematiska objekt kan inte ses; de kan inte visualiseras; de kan inte ha någon utökad – eller ”faktisk” – form. Om ett objekt faktiskt har form, om det tar plats, måste det bestå av rumsligt utökade objekt som liknar datorpixlar, inte matematiska punkter.
OBS: Jag pratar inte bara om” fysiskt utrymme ”eller”fysisk form”. Jag pratar om former av något slag. Det jag ser i mitt synfält – blobbar av färg-har form, men de är inte fysiska föremål. De själva upptar inte fysiskt utrymme. De är mentala representationer, och de består av utökade ljuspunkter – pixlar på min mentala skärm.
så uppstår en naturlig fråga:
har någon någonsin sett eller upplevt dessa matematiska former på något sätt? Har någon stött på en enda sann ”linje”eller ” cirkel”? Svaret måste vara ett eftertryckligt ” Nej.”Alla ” linjer” och ”cirklar” som vi faktiskt upplever har dimensioner. De är konstruerade från ett begränsat antal punkter som själva har dimensioner. Objekten vi upplever består av pixlar.
betydelsen av denna punkt kan inte överdrivas.
det betyder att varje ”cirkel” du någonsin sett – eller någon ingenjör någonsin har lagt ner på papper – faktiskt har ett rationellt förhållande mellan dess omkrets och dess diameter. Varje ” cirkel ”som någonsin har stött på har en unik” pi ” som kan uttryckas som förhållandet mellan två heltal.
”omkrets”, för varje cirkel vi kan uppleva, kan förstås som” formens yttersta gräns”, som i sig består av ett begränsat antal pixlar. Det är ”diameter” är också ett enkelt heltal – antalet pixlar som komponerar det. Sätt ett heltal som en täljare och ett heltal som nämnare, och du har en rationell pi.
faktum är att dessa sanningar bör vara okontroversiella, även för matematiker:
varje ”cirkel” du någonsin har stött på, utan undantag, har en rationell, ändlig pi.
ingen ”cirkel” du någonsin har stött på, utan undantag, har en irrationell pi.
så det betyder att mina påståenden om en” rationell pi ”är sanna för minst 99,9999% av alla former som vi kallar”cirklar”. Det betyder också att pi är unik för en viss cirkel. Detta bör inte komma som en överraskning, dock, när man tänker på vilken typ av förhållanden.
Tänk dig att jag skulle säga, ” Vad är förhållandet mellan ett bords höjd och längd?”
du skulle naturligtvis svara, ” vilken tabell?”
detsamma gäller cirklar. Det finns inget ”ett sant förhållande som kallas” pi ””av samma anledning finns det inget” ett sant förhållande mellan en tabells höjd och längd.”Varje tabell och cirkel är konstruerad av ett begränsat antal enheter, ordnade på olika sätt, och därför kommer deras förhållanden att variera.
enligt standardgeometri finns det bokstavligen bara en” cirkel ”som mina påståenden inte stämmer för: den så kallade” perfekta cirkeln ” -ett objekt så mystiskt att ingen dödlig någonsin har stött på den.
den gudomliga formen
denna ”perfekta cirkel” har inga mätbara sidor eller kanter. Dess gräns består av ett oändligt antal nolldimensionella punkter. De yttersta punkterna tar upp exakt nollutrymme. Dess pi kan inte uttryckas med någon decimal expansion – inte heller kommer vi någonsin att veta exakt vad dess pi är.
detta objekt kan inte konstrueras, visualiseras eller ens existera i vår värld. Vår värld är för ofullkomlig för den. Istället lever den i en annan värld som våra sinnen svagt kan komma åt.
den perfekta cirkeln är så stor att alla andra” cirklar ” bara är approximationer av den. Det är den enda sanna cirkeln. Om du ber om bevis på dess existens, hittar du ingen. Ändå har matematikerna byggt hela sin geometriska teori baserat på dess existens.
Jag erkänner fritt min kätteri: jag tror inte på den ”perfekta cirkeln.”
därför tror jag inte på ” irrationell pi.”Jag har inte heller något behov av ett sådant koncept. Varje form jag någonsin har stött på – eller någonsin kommer att stöta på-har kanter som tar plats.
en geometri utan perfekta cirklar och utan irrationell pi är helt tillräcklig för att förklara alla fenomen jag upplever. Därför behöver jag inte placera en extra enhet – särskilt en med sådana anmärkningsvärda egenskaper.
med andra ord: Jag tror helt enkelt på en mindre cirkel än matematiker. Det är allt som krävs för att dra slutsatsen att pi är ett rationellt tal för en given cirkel.
bara en abstraktion!
Jag har hört att vissa matematiker hävdar att geometriska objekt bara är abstraktioner och därför är undantagna från föregående kritik. Men bland annat får detta abstraktionens metafysik bakåt. Du abstrakt från concretes. Du behöver inte konkreta från abstrakt.
Tänk på det. Från vad gör en abstrakt för att få begreppet ”perfekt cirkel”?
det kan inte vara de cirklar vi faktiskt ser, eftersom var och en av dessa cirklar har ofullkomliga kanter. Alla konkreta upplevelser vi har är av former med ofullkomliga kanter, en rationell pi och består av punkter med dimension. Så från dessa erfarenheter säger matematikern: ”Tja, jag tror att en sann cirkel är en utan kanter, med en irrationell pi, och består av nolldimensionella punkter!”
detta är nonsens, och det är inte så abstraktion fungerar.
Tänk dig att vi pratar om hus och abstrakta föreställningar om hus.
varje hus vi någonsin har stött på har väggar, ett golv och ett tak. Matematikern vill säga att hans uppfattning om ett” perfekt hus ” är ett utan väggar, golv eller tak. Och i själva verket är vanliga olhus bara approximationer av hans perfekta hus. Självklart är detta ett misstag.
Vi kan ha en helt giltig abstrakt uppfattning om ett hus, men egenskaperna hos vårt ”abstrakta hus” måste inkludera egenskaperna hos de betonghus vi abstraherar från. Vårt ” mentala hus ”måste inkludera de konceptuella kategorierna” att ha väggar, golv, och ett tak.”Dimensionerna på dessa egenskaper är irrelevanta, så länge de finns.
en abstrakt uppfattning om” ett hus utan väggar, golv eller tak ” kan inte förklara några fenomen vi upplever, eftersom det inte beskriver något som eventuellt kan existera. Tänk dig att din vän tar dig till ett tomt fält och säger: ”här är mitt perfekta hus! Det har inga väggar, golv eller tak!”Du skulle tro att han var galen-speciellt om han tillade, ”Och alla andra hus är bara en approximation av det!”
inte riktigt!
ett av de mer självinkriminerande svaren från matematiker går så här, ” men matematiska objekt är inte riktiga! De finns inte alls!”I all min forskning kan jag med säkerhet säga att matematik är det enda tankeområdet där man medger att” föremålen jag pratar om inte är verkliga och inte existerar ” är tänkt att försvara en viss teori.
detta fel är en sammanblandning av objekt och deras referenser. Till exempel ska begreppet ”mitt hus” hänvisa till ”mitt hus i världen.”Det skulle vara dumt att säga ”mitt hus tar inte plats, för min uppfattning om mitt hus tar inte plats.”
på samma sätt ska uppfattningen av en” punkt ”hänvisa till” en exakt plats i geometriskt utrymme.”Det skulle vara lika dumt att säga” poäng tar inte upp geometriskt utrymme, för min uppfattning om en punkt tar inte upp geometriskt utrymme.”
geometriens grundläggande väsen handlar om rymden-vare sig det är fysiskt utrymme, mentalt utrymme, konceptuellt utrymme eller någon annan typ av utrymme. Därför måste geometriens föremål själva ta plats. Det finns inget sådant som ” en exakt plats i rymden som inte är en exakt plats i rymden.”
en alternativ teori
så låt mig presentera en alternativ geometrisk ram. Detta är bara början på en helt ny teori om matematik som jag kallar ”basenhet matematik.”Detta är grunden för basenhetens geometri:
1) alla geometriska strukturer består av basenheter. Dessa enheter kallas ” poäng.”
2) varje punkt är rumsligt utsträckt.
3) i alla konceptuella ramar är förlängningen av basenheten exakt 1. Inom denna ram Finns det ingen mindre enhet av avstånd, per definition.
4) alla avstånd och former kan benämnas i termer av basenheten.
dessa fundament utgör en logiskt sund grund för att bygga geometri.
Sätt ihop punkter, och du kan komponera vilken form du vill, utan några irrationella tal. Varje objekt utom basenheten är ett sammansatt objekt som består av diskreta punkter. Det är därför jag sa tidigare att jag gillar Euclids ursprungliga definition av en ”punkt” som ”det som inte har någon del.”Basenheter har inga delar; de är de delar som bildar varannan helhet.
Jag inser att det kommer att finnas massor av invändningar mot detta sätt att tänka på geometri. Dessa invändningar kommer att behandlas i detalj i framtida artiklar.
för att få en intuition om detta ramverk kan du tänka på ”poäng” som ”pixlar”, som vi alla har erfarenhet av. Alla former och objekt som du kan stöta på i en hi-res VR-simulering är faktiskt klumpar av pixlar, även om de kan verka ”helt släta” ur vårt makroskopiska perspektiv.
några av de fina konsekvenserna av denna teori:
detta är en rad:

detta är en cirkel:

och den har en bevisligen rationell pi:
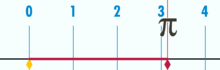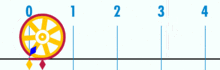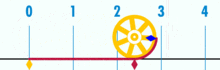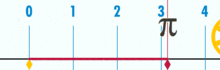
(Obs: Denna GIF togs från Wikipedia för att visa den förmodade irrationaliteten hos pi. Men om du är medveten om vad du tittar på är det faktiskt en demonstration av Pi: s rationalitet. Du tittar på en GIF av den logiska perfektion och precision basenhet geometri!)
vad är förhållandet mellan denna cirkels omkrets och diameter? Enkelt: det är ett heltal över ett annat-men många basenheter utgör omkretsen, dividerat med hur många enheter som utgör diametern. Och, som det så händer, så länge cirkeln inte är konstruerad av en liten mängd basenheter, kommer pi-förhållanden att fungera till cirka 3.14159 (men om vi är helt exakta måste vi beteckna i termer av fraktioner, eftersom decimalutvidgning kan vara tvivelaktig inom en basenhetsram. Men det är en framtida artikel.). Det finns ingen ”generisk” eller ”idealisk” cirkel. Det finns konkreta, faktiska cirklar, som var och en är ett sammansatt objekt konstruerat av ett begränsat antal punkter.
det betyder bland annat att det inte finns något sådant som en ”enhetscirkel” – en förmodad cirkel med en radie av 1. Det finns inga diametrar som har ett avstånd på 1. Du kan inte skapa en cirkel med bara en pixel.
inom denna teori är ”cirklar” exakt vad du har stött på. ”Poäng ”är platser i rymden som är faktiska platser i rymden, och” linjer ” är vad alla vet att de är.
basenhet Intuition
uppenbarligen kräver detta ämne mycket mer förklaring och arbete, inte bara i geometri, men överallt som matematikens metafysik är felaktig. Jag kan inte täcka alla invändningar mot basenhetsgeometri i den här artikeln, men jag kommer att förklara några fler sätt att tänka på det och varför det är överlägset standardortodoxi.
först och främst förklarar detta ramverk alla fenomen vi upplever, och det förlorar exakt noll förklarande kraft jämfört med standardgeometri. Varje form, varje cirkel, varje linje, varje punkt, varje rumslig upplevelse som vi någonsin kommer att ha kan förklaras utan att det finns extra enheter. Vi upplever inte perfekta cirklar; därför har vi ingen anledning att teoretisera om dem.
dessutom är basenhetens matematik mer logiskt exakt än ortodoxin. Alla som har arbetat med” irrationell pi ” måste använda approximationer. De kan inte använda en faktisk oändlig decimal expansion. De tvingas godtyckligt skära av storleken för pi för att kunna använda den. Inte så med basenhet geometri. Perfekt precision är faktiskt möjligt, eftersom det inte finns några approximationer eller oändliga decimalutvidgningar att hantera. Det här kanske inte är en stor sak just nu, men när tekniken närmar sig basenhetens dimensioner av fysiskt utrymme kan det faktiskt göra stor skillnad.
Här är en kort, intressant sida om pi: s oändliga decimalutvidgning:
vad händer när ortodoxa matematiker beräknar ytterligare och ytterligare decimaler av pi? Fattar de på”den perfekta cirkelns sanna förhållanden”? Nej. Vad de gör är att beräkna pi-förhållandena för cirklar med allt mindre basenheter. När basenheten krymper – eller när cirkeln blir större i diameter-förändras förhållandet mellan dess omkrets och diameter allt så lite. Dessa beräkningar är omedelbart praktiska, på samma sätt som trig-tabeller är praktiska. De är förkalkylerade värden som är tillämpliga och korrekta för en given cirkel av en given storlek.
(om du vill förstå varför pi ändras något, tänk på det så här: när storleken på basenheten ökar, krymper området som omges av omkretsen; när storleken på basenheten minskar ökar området som omges av omkretsen, men ändå i en minskande takt. Ju mjukare kanten på cirkeln är, desto större är cirkelns yta.)
på denna anmärkning: basenhetens geometri kräver inte en ” ultimat basenhet.”Med andra ord kommer varje konceptuellt system att ha en basenhet av logisk nödvändighet, men det betyder inte att du hindras från att komma med ett annat konceptuellt system som har en mindre basenhet.
Tänk på det så här: ett visst fotografi kommer att innehålla ett begränsat antal pixlar. Det kommer att ha en basenhet upplösning. Men det betyder inte att det är omöjligt att ta ett foto med högre upplösning. på samma sätt kommer en viss cirkel att ha en basenhetsupplösning, men det betyder inte att det är omöjligt att tänka på en med högre upplösning (mindre basenheter).
Vi kan till och med stöta på gränserna för den fysiska världen. Det fysiska rummet måste ha en basenhet, vilket innebär att det inte finns någon mindre enhet inom vårt fysiska system. Men det betyder inte att vi hindras från att prata om mindre dimensionella basenheter. Dessa objekt kommer helt enkelt inte att korrelera med vårt universum. Vem vet – kanske kan vi säga sanna saker om ett annat fysiskt universum som har mindre basenheter.
Obs: Detta korrelerar också perfekt med min upplösning till Zenos paradoxer. Utrymmet måste ha en basenhet, om rörelse är möjlig.
ett bra exempel på basenhetsfenomen är fraktalen. Förment, fraktaler är bara vettiga inom den konceptuella ramen för ” oändlig delbarhet.”Detta är inte korrekt. Fraktaler ger mycket mer mening inom ett basenhetskontext. Tänk på den här bilden:

det här ser ut som en främsta kandidat för ” oändlig delbarhet.”Men det är en illusion. Vid varje given tidpunkt finns det en basenhet upplösning på den här bilden. När bilden ”zoomar in” skapas nya enheter, alla benämnda i form av pixlar. Du tittar inte på oändligheten; du tittar alltid på ett begränsat antal pixlar. Om du tvivlar på detta kan du räkna pixlarna. Objektet byggs när du tittar på det. Samma sak händer i matematik; föremålen blir konstruerade när du tänker på dem. Mycket mer kommer att sägas om detta i framtida artiklar.
polygoner och greker
Jag vill snabbt ta itu med en invändning som oundvikligen kommer att uppstå – de som hävdar att bilderna av cirklar i den här artikeln inte är cirklar; de är polygoner. Kanterna är en massa små raka linjer; de är inte helt släta. Om detta är sant är det ingen kritik av basenhetens geometri, eftersom alla runda objekt som vi stöter på skulle vara polygoner. Därför bör våra matematiska teorier handla om polygoner; vi upplever inget annat. Jag vill veta om egenskaperna hos denna form:

Jag bryr mig inte vad du kallar det. Basenhetens geometri kan berätta om egenskaperna hos den formen.
grekerna gjorde också detta misstag när de pratade om cirklar-som om de var konstruerade av ett ”oändligt antal linjer.”Detta är felaktigt. Cirklar och polygoner består av ett begränsat antal punkter, inte linjer. Linjer komponerar ingenting; de är själva sammansatta objekt.
Tänk dig att bygga en cirkel i sanden.

vad är området för denna cirkel? Jag garanterar att det är ett ändligt, rationellt tal. Du kan bokstavligen räkna sandkornen som komponerar den. Omkretsen består av sandkorn, liksom diametern, liksom området. De är alla heltal.
det sista argumentet jag kommer att ta upp i artikeln kommer från dem som tycker att en ”cirkel” inte är en form; det är ett matematiskt uttryck. Något som (x2 + y2 = r2).
detta är bara en annan metafysisk förvirring som sammanfogar symboler med objektet som symbolerna ska beskriva. Det är som att säga ”äpplen” är synonymt med orden ” en röd frukt.””Detta är förvirrat. Orden ”en röd frukt” är en beskrivning av objektet, inte själva objektet. Formeln som (x2 + y2 = r2) kommer att beskriva formen på en cirkel – eller, om du föredrar att tänka på det här sättet – det är en regel för att bygga en cirkel. Det är inte i sig en cirkel.
det är där jag avslutar den här artikeln. Det finns mycket mer att säga i framtiden. Matematik är inte befriad från kritik eller skeptisk utredning. Det är inte heller befriat från behovet av exakt metafysik. Av alla skäl som jag skisserade i det här inlägget finns det gott om utrymme för alternativa och överlägsna begrepp om geometri. Basenhetens geometri förlorar ingen förklarande kraft, eliminerar ett oändligt antal onödiga objekt och ger en logisk grund för att bygga en starkare teori.
om du inte tror på förekomsten av ”perfekta cirklar” – som består av ett oändligt antal nolldimensionella punkter-tror du inte att pi är irrationell, och du har gått med i en extremt liten grupp intellektuella spetälska. Du kan nu förvänta dig hån och fördömande för din kätteri.
Om du gillade den här artikeln och vill stödja skapandet av mer kätteri, besök patreon.com/stevepatterson.