3.3 Der Carnot-Zyklus | Maybaygiare.org

Weiter: 3.4 Kühlschränke und Aufheizen: 3. Das erste Gesetz Zurück: 3.2 Verallgemeinerte Darstellung des Inhalts Index

Ein Carnot-Zyklus ist in Abbildung 3.4 dargestellt. Es hasfour Prozesse. Es gibt zwei adiabatische reversible Beine und zweiisothermische reversible Beine. Wir können einen Carnot-Zyklus mit konstruierenviele verschiedene Systeme, aber die Konzepte können mit einem bekannten Arbeitsfluid, dem idealen Gas, gezeigt werden. Das System kann als angesehen Werdenkammer, die von einem Kolben umschlossen und mit diesem idealen Gas gefüllt ist.

Abbildung 3.4:Carnot-Zyklus – thermodynamisches Diagramm links und schematische Darstellung der verschiedenen Phasen des Zyklus für ein System, das aus einem idealen Gas auf der rechten Seite besteht

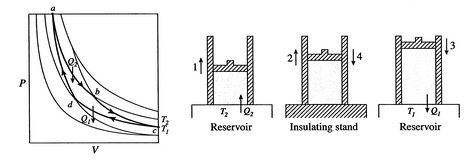
Die vier Prozesse im Carnot-Zyklus sind:

Das System hat die Temperatur 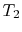im Zustand . Es isbrought in Verbindung mit einem Wärmespeicher, der gerade eine Flüssigkeit orsolid Masse des genügend großen Umfangs ist, damit seine Temperatur notchange merklich, wenn irgendeine Wärmemenge thesystem übertragen wird. Mit anderen Worten, der Wärmespeicher ist eine konstante Temperaturquelle (oder Empfänger) von Wärme. Das System erfährt dann eine anisotherme Expansion von zu , wobei Wärme absorbiert wird .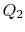
Atstate wird das System thermisch isoliert (vom Kontakt mit dem Wärmespeicher entfernt) und dann auf expandieren lassen. Während dieser Ausdehnung sinkt die Temperatur auf . Die Wärme ausgetauschtwährend dieses Teils des Zyklus, $Q_{bc}=0.$ )
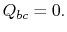Im Zustand Das System wird in Kontakt mit einem Wärmespeicher bei der Temperatur gebracht . Es wird dann komprimiert, um 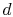anzugeben und dabei heat 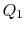abzulehnen.
Schließlich wird das System adiabatisch zurück in den Ausgangszustand komprimiert . Der Wärmeaustausch $Q_{da}=0$ .

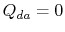Der thermische Wirkungsgrad des Zyklus ist gegeben durch die Definition

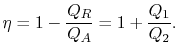$\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$

(3..4)

In dieser Gleichung ist eine Vorzeichenkonvention impliziert. Die Größen wie definiert sind die Größen der absorbierten und projizierten Wärme. Die Mengen hingegen werden in Bezug auf die vom System empfangene Wärme definiert. In diesem Beispiel ist ersterer negativ und letzterer positiv. Die vom System absorbierte und projizierte Wärme findet während isothermer Prozesse statt undWir wissen bereits, welche Werte sie von Gl.(3.1):

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 ,$

$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\quad \textrm{ ($Q_1$ ist negativ.)}$

Die Effizienz kann nun in Bezug auf die Volumina in den verschiedenen Zuständen geschrieben werden als

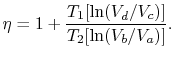$\displaystyle \eta = 1+ \frac{T_1}{T_2}.$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) zeigt zwei Konsequenzen. Erstens beziehen sich die empfangenen und abgelehnten Wärmeauf die Temperaturen der isothermen Teile des Zyklus durch

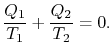$\displaystyle \frac{Q_1}{T_1}+\frac{Q_2}{T_2}= 0.$

(3..6)

Zweitens ist die Effizienz eines Carnot-Zyklus kompakt gegeben durch

$\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad\textbf{Carnot-Zykluseffizienz.}$

(3..7)

Der Wirkungsgrad kann nur dann 100% betragen, wenn die Temperatur, bei der die Wärme zurückgewiesen wird, Null ist. Die Wärme- und Arbeitsübertragungen zum und vom System sind schematisch in Abbildung 3.5 dargestellt.

Abbildung 3.5:Arbeit und Wärmeübertragungen inein Carnot-Zyklus zwischen zwei Wärmespeichern

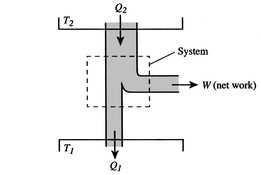
Schlammige Punkte

Seit $\eta = 1- {T_1}/{T_2}$ , Blick auf die graph, doesthat bedeuten die weiter auseinander die isothermen sind, thegreater effizienz? Und wenn sie sehr nah wären, wäre essehr ineffizient? (MP 3.2)

Warum haben wir es im Carnot-Zyklus nur mit Volumenänderungen und nicht mit Druckänderungen an den Adiabaten und Isothermen zu tun?(MP 3.3)

Gibt es eine physikalische Anwendung für den Carnot-Zyklus? Können wir einen Carnot-Motor für ein Antriebsgerät entwerfen?(MP 3.4)

Woher wissen wir, welche Zyklen als Modelle für reale Prozesse verwendet werden sollen?(MP 3.5)

Weiter: 3.4 Kühlschränke und Aufheizen: 3. Das erste Gesetz Previous: 3.2 Verallgemeinerte Darstellung des Inhaltsindex

UnifiedTP

Maybaygiare.org

Schreibe einen Kommentar Antworten abbrechen