Definition
Ein Polynom in der Variablen x ist eine Funktion, die in der Form geschrieben werden kann,
wobei an, an-1 , …, a2, a1, a0 sind Konstanten. Wir nennen den Term, der die höchste Potenz von x (d. H. anxn ) enthält, den führenden Term und wir nennen an den führenden Koeffizienten. Der Grad des Polynoms ist die Potenz von x im führenden Term. Wir haben bereits Polynome des Grades 0, 1 und 2 gesehen, die die konstanten, linearen und quadratischen Funktionen waren. Grad 3, 4 und 5 Polynome haben auch spezielle Namen: kubische, quartische und quintische Funktionen. Polynome mit dem Grad n > 5 werden nur Polynome n-ten Grades genannt. Die Namen der verschiedenen Polynomfunktionen sind in der folgenden Tabelle zusammengefasst.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
Das Grenzverhalten von Polynomen
Das Grenzverhalten einer Funktion beschreibt, was mit der Funktion als x → ±∞ passiert. Der Grad eines Polynoms und das Vorzeichen seines führenden Koeffizienten bestimmen sein begrenzendes Verhalten. Insbesondere
Diese Ergebnisse sind in der folgenden Tabelle zusammengefasst.
Sie können diese Informationen verwenden, um festzustellen, ob ein Polynom einen ungeraden oder geraden Grad hat und ob der führende Koeffizient positiv oder negativ ist, indem Sie einfach seinen Graphen untersuchen.
Die folgenden Graphen von Polynomen veranschaulichen jedes der in der obigen Tabelle beschriebenen Verhaltensweisen.
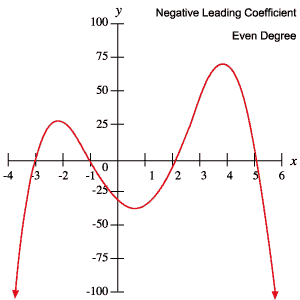
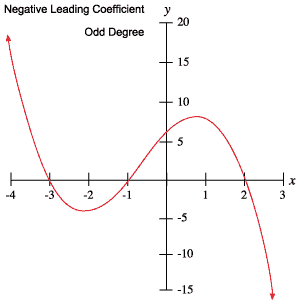
Wurzeln und Wendepunkte
Der Grad eines Polynoms sagt noch mehr darüber aus als das Begrenzungsverhalten. Insbesondere kann ein Polynom n-ten Grades höchstens n reelle Wurzeln (x-Abschnitte oder Nullen) haben, die Multiplizitäten zählen. Angenommen, wir betrachten ein Polynom 6. Grades mit 4 verschiedenen Wurzeln. Wenn zwei der vier Wurzeln die Multiplizität 2 und die anderen 2 die Multiplizität 1 haben, wissen wir, dass es keine anderen Wurzeln gibt, weil wir alle 6 Wurzeln berücksichtigt haben. Dies liegt daran, dass die Wurzeln mit einer Vielzahl von zwei (auch als Doppelwurzeln bezeichnet) als zwei Wurzeln gezählt werden.Beachten Sie, dass ein Polynom n—ten Grades nicht n reelle Wurzeln haben muss – es könnte weniger haben, weil es imaginäre Wurzeln hat. Beachten Sie, dass ein Polynom ungeraden Grades mindestens eine reelle Wurzel haben muss, da sich die Funktion an einem Ende – ∞ und am anderen Ende + ∞ nähert; eine stetige Funktion, die von negativ zu positiv wechselt, muss die x-Achse irgendwo dazwischen schneiden. Zusätzlich kann ein Polynom n-ten Grades höchstens n – 1 Wendepunkte aufweisen. Ein Wendepunkt ist ein Punkt, an dem sich die Funktion von steigend zu abnehmend oder abnehmend zu steigend ändert, wie in der folgenden Abbildung dargestellt. Auch hier muss ein Polynom n-ten Grades keine n – 1 Wendepunkte haben, es könnte weniger haben.
Hinweis zur Vorsicht
Es ist wichtig, den Unterschied zwischen geraden und ungeraden Funktionen und Polynomen geraden und ungeraden Grades zu erkennen. Jede Funktion, f(x), ist entweder even if,
f(−x) = x,
für alle x in der Domäne von f(x), oder odd if,
f(−x) = −x,
für alle x in der Domäne von f(x), oder weder even noch odd , wenn keine der obigen Aussagen wahr ist. Ein Polynom k-ten Grades, p(x), soll einen geraden Grad haben, wenn k eine gerade Zahl ist, und einen ungeraden Grad, wenn k eine ungerade Zahl ist. Denken Sie daran, dass selbst wenn p (x) einen geraden Grad hat, es nicht unbedingt eine gerade Funktion ist. Wenn p (x) einen ungeraden Grad hat, ist es nicht unbedingt eine ungerade Funktion.
Wir verwenden auch die Begriffe gerade und ungerade, um Wurzeln von Polynomen zu beschreiben. Insbesondere hat ein Polynom p (x) die Wurzel x = a der Multiplizität k (dh x = a ist eine k−mal wiederholte Wurzel), wenn (x – a) k ein Faktor von p (x) ist. Wir sagen, dass x = a eine gerade Multiplizität hat, wenn k eine gerade Zahl ist, und eine ungerade Multiplizität, wenn k eine ungerade Zahl ist.
Domäne und Bereich
Alle Polynome haben dieselbe Domäne, die aus allen reellen Zahlen besteht. Der Bereich der Polynome ungeraden Grades besteht auch aus allen reellen Zahlen. Der Bereich der Polynome geraden Grades ist etwas komplizierter und wir können den Bereich aller Polynome geraden Grades nicht explizit angeben. Wenn der führende Koeffizient positiv ist, erstreckt sich die Funktion auf + ∞; Wenn der führende Koeffizient negativ ist, erstreckt er sich auf – ∞. Dies bedeutet, dass sogar Gradpolynome mit positivem führenden Koeffizienten einen Bereich haben, in dem ymax das globale Maximum bezeichnet, das die Funktion erreicht. Im Allgemeinen ist es nicht möglich, die Maxima oder Minima von Polynomen analytisch zu bestimmen.
*****
Im nächsten Abschnitt lernen Sie die Polynomdivision, eine Technik, mit der Sie die Wurzeln von Polynomfunktionen finden.
Polynomteilung