Das Skalendreieck ist ein Dreieck mit allen Seiten unterschiedlicher Länge.
Alle Winkel sind auch unterschiedlich.
Also sind keine Seiten gleich und keine Winkel sind gleich.
Formel für die Fläche des Skalendreiecks :
= √
wobei
S = (a + b + c) / 2
Hier sind a, b und c Seitenlängen des Dreiecks.
Übungsprobleme
Problem 1 :
Finden Sie die Fläche des Skalendreiecks, dessen Seitenlänge 12 cm, 18 cm und 20 cm beträgt.
Lösung :
Da die Längen der drei Seiten unterschiedlich sind, ist das Dreieck ein skaliertes Dreieck.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25x13x7x5)
= 5√455
Also, Fläche des gegebenen Skalendreiecks ist 5 √455 Quadratzentimeter.
Problem 2:
Die Seiten eines Skalendreiecks sind 12 cm, 16 cm und 20 cm. Finde die Höhe zur längsten Seite.
Lösung :
Um die Höhe zur längsten Seite eines Dreiecks zu finden, müssen wir zuerst die Fläche des Dreiecks finden.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
finden Sie die Höhe zur längsten Seite, die längste Seite ist die Basis des Dreiecks, wie unten gezeigt.
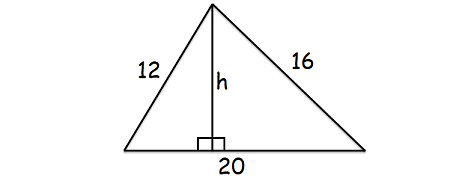
Hier ist die längste Seite 20 cm.
Fläche des obigen Dreiecks = 96 cm2
(1/2) x 20 x h = 96
10h = 96
Teilen Sie jede Seite durch 10.
h = 9,6 cm
Die Höhe zur längsten Seite beträgt also 9,6 cm.
Problem 3:
Die Seiten eines Skalendreiecks sind im Verhältnis (1/2) : (1/3) : (1/4). Wenn der Umfang 52 cm beträgt, ermitteln Sie die Länge der kleinsten Seite.
Lösung :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length die kleinste Seite beträgt 12 cm.
Problem 4 :
Die Fläche des Scalene-Dreiecks beträgt 216 cm2 und die Seiten haben das Verhältnis 3 : 4 : 5. Finde den Umfang des Dreiecks.
Lösung :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
Umfang des gegebenen Skalendreiecks ist
= 18 + 24 + 30
= 72 cm
Problem 5 :
Eine Seite eines rechtwinkligen Skalendreiecks ist doppelt so groß wie die andere, und die Hypotenuse beträgt 10 cm. Finde die Fläche des Dreiecks.
Lösung :
Sei ‚x‘ die Länge eines der Beine des Dreiecks.
Dann ist die Länge des anderen Beines 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2)(x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

Abgesehen von den oben genannten Dingen, wenn Sie andere Dinge in Mathe benötigen, verwenden Sie bitte unsere benutzerdefinierte Google-Suche hier.
Wenn Sie Feedback zu unseren mathematischen Inhalten haben, senden Sie uns bitte eine E-Mail:
Wir freuen uns immer über Ihr Feedback.
Sie können auch die folgenden Webseiten zu verschiedenen Themen in Mathe besuchen.
WORTPROBLEME
HCF- und LCM-Wortprobleme
Wortprobleme mit einfachen Gleichungen
Wortprobleme mit linearen Gleichungen
Wortprobleme mit quadratischen Gleichungen
Algebra-Wortprobleme
Wortprobleme mit Zügen
Flächen- und Umfangs-Wortprobleme
Textaufgaben zur direkten Variation und inversen Variation
Textaufgaben zum Stückpreis
Textaufgaben zum Stückpreis
Textaufgaben zum Vergleichen von Raten
Umrechnen üblicher Einheiten Textaufgaben
Umrechnen metrischer Einheiten Wortaufgaben
robleme
Wortprobleme auf einfache Interesse
Wortprobleme auf Zinseszins
Wortprobleme auf Arten von Winkeln
Komplementäre und ergänzende Winkel Wortprobleme
Doppel Fakten Wortprobleme
Trigonometrie Wortprobleme
Prozentsatz Wortprobleme
Gewinn und Verlust Wortprobleme
Markup und Markdown Wortprobleme probleme
Dezimale Wortprobleme
Wortprobleme mit Brüchen
Wortprobleme mit gemischten Fraktrionen
Ein-Schritt-Gleichung Wortprobleme
Lineare Ungleichungen Wortprobleme
Verhältnis und proportion Wortprobleme
Zeit und Arbeit Wortprobleme
Wortprobleme auf Sets und Venn-Diagramme
Wortprobleme auf Alter
Satz des Pythagoras Wortprobleme
Prozent einer Zahl Wortprobleme
Wortprobleme auf konstanter Geschwindigkeit
Wortprobleme auf Durchschnittsgeschwindigkeit
Wortprobleme auf Summe der Winkel eines Dreiecks ist 180 Grad
WEITERE THEMEN
Gewinn- und Verlustverknüpfungen
Prozentverknüpfungen
Zeittabellenverknüpfungen
Zeit-, Geschwindigkeits- und Entfernungsverknüpfungen
Verhältnis- und Proportionsknüpfungen
Domänen- und bereich rationaler Funktionen
Domäne und Bereich rationaler Funktionen mit Löchern
Grafische Darstellung rationaler Funktionen
Grafische Darstellung rationaler Funktionen mit Löchern
Konvertieren sich wiederholender Dezimalzahlen in Brüche
Dezimaldarstellung rationaler Zahlen
Quadratwurzel mit langer Division finden
L.C.M Methode zur Lösung von Zeit- und Arbeitsproblemen
Übersetzen der Wortprobleme in algebraische Ausdrücke
Rest, wenn 2 Potenz 256 durch 17 geteilt wird
Rest, wenn 17 Potenz 23 durch 16 geteilt wird
Summe aller dreistelligen Zahlen, die durch 6 teilbar sind
Summe aller dreistelligen Zahlen, die durch 7 teilbar sind
Summe aller durch 8 teilbare Zahlen
Summe aller dreistelligen Zahlen, die mit 1, 3, 4 gebildet wurden
Summe aller drei vierstelligen Zahlen, die mit Ziffern ungleich Null gebildet wurden
Summe aller drei vierstelligen Zahlen, die mit 0, 1, 2, 3 gebildet wurden
Summe aller drei vierstelligen Zahlen gebildet mit 1, 2, 5, 6