Expertise: Intermediate
Was ist eine Spline-Funktion?
Wir müssen wissen, was die wesentlichen Eigenschaften von Splines sind, bevor wir überlegen, wie wir ein Basissystem für sie konstruieren können.
Spline-Funktionen werden gebildet, indem Polynome an festen Punkten, Knoten genannt, zusammengefügt werden. Das heißt, wir teilen das Intervall, das sich von der unteren Grenze tL bis zur oberen Grenze tU erstreckt, über die wir eine Kurve approximieren möchten, in L + 1 Unterintervalle, die durch L innere Grenzen Tll getrennt sind, die Knoten oder manchmal Haltepunkte genannt werden.)Es gibt einen Unterschied zwischen diesen beiden Begriffen, aber wir werden später darauf kommen.
Betrachten Sie den einfachsten Fall, in dem ein einzelner Haltepunkt das Intervall in zwei Unterintervalle unterteilt. Die Splinefunktion ist innerhalb jedes Intervalls ein Polynom bestimmten Grades (die höchste Potenz, die das Polynom definiert) oder Ordnung (die Anzahl der Koeffizienten, die das Polynom definieren, die eins mehr istals sein Grad). Verwenden wir m, um die Reihenfolge des Polynoms zu bezeichnender Grad ist m – 1:
Am inneren Haltepunkt m1 müssen sich die beiden Polynome reibungslos verbinden. Im gebräuchlichsten Fall bedeutet dies, dass die Ableitungen bis zur Ordnung eins weniger als der Grad übereinstimmen. Wenn sie mit der Ableitung übereinstimmten, deren Reihenfolge dem Grad entsprach, wären sie tatsächlich dasselbe Polynom. Somit hat eine so definierte Spline-Funktion einen zusätzlichen Freiheitsgrad als ein sich über das gesamte Intervall erstreckendes Polynom.Zum Beispiel sei jedes Polynom ein gerades Liniensegment und daher vom Grad eins. Dabei verbinden sie sich am Haltepunkt mit übereinstimmenden Derivatenbis zu Grad 0; Kurz gesagt, sie verbinden sich einfach und haben identische Werte am Haltepunkt. Da das erste Polynom zwei Freiheitsgrade (Steigung und Schnittpunkt) hat und das zweite, dessen Wert bereits am Haltepunkt definiert ist,nur einen Freiheitsgrad (Steigung)aufweist, hat die gesamte Polygonlinie dreifreiheitsgrade.
Dementsprechend, wenn beide Polynome quadratisch sind, dann ist die Übereinstimmung sowohl in Bezug auf die Werte als auch in Bezug auf Dieneigung der ersten Ableitungin ξ1. Das erste Polynom hat drei Freiheitsgrade, aber thesecond verliert zwei, weil ifthe Beschränkung auf seinen Wert und Steigung bei ξi, und behält somit onlyone. Damit verbleiben insgesamt vier Freiheitsgrade für die so gebildete Splinefunktion, im Gegensatz zu drei für ein quadratisches Polynom über das gesamte Intervall. Abbildung 1 zeigt theselinear und quadratische Fälle mit einem einzigen Haltepunkt.
Was sind einige Beispiele für häufig verwendete Basisfunktionen?
Wir können nun die Situation verallgemeinern, um L innere Haltepunkte, anda Spline-Funktion der Ordnung m oder Grad m – 1 über eachsub-Intervall. Das erste Polynomsegment hat ein vollständiges Komplement von m Freiheitsgraden, aber jedes nachfolgende Segment hat aufgrund der m – 1-Einschränkungen seines Verhaltens nur einen Freiheitsgrad.Dies ergibt insgesamt L + m Freiheitsgrade oder Anzahl der inneren Haltepunkte plus die Reihenfolge der Polynomsegmente.
Spline-Funktionen sind also im Wesentlichen Verallgemeinerungen des Begriffs Polygonallinien. Sie gewinnen ihre Flexibilität auf zwei Arten: Erstens durch die Reihenfolge der Polynome, aus denen sie aufgebaut sind, und zweitens durch die Anzahl der verwendeten Haltepunkte. Wir entscheiden uns normalerweise dafür, die Reihenfolge beizubehalten und Haltepunkte hinzuzufügen, um die erforderliche Flexibilität zu erhalten.
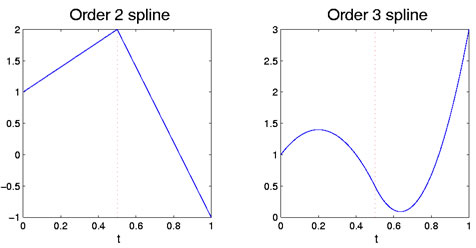
Abbildung 1: Die linke Abbildung zeigt eine Ordnung zwei Spline-Funktion, whichis stückweise linear. Die rechte Figur ist ein Spline der Ordnung 3, derist stückweise quadratisch. Thebreakpoint bei 0,5 wird durch die rote vertikale gestrichelte Linie angezeigt.