Maßstab (Karte)

Wie Gauss ‚Theorema Egregium beweist, kann eine Kugel (oder ein Ellipsoid) nicht verzerrungsfrei auf eine Ebene projiziert werden. Dies wird allgemein durch die Unmöglichkeit veranschaulicht, eine Orangenschale auf eine flache Oberfläche zu glätten, ohne sie zu reißen und zu verformen. Die einzig wahre Darstellung einer Kugel in konstantem Maßstab ist eine andere Kugel wie ein Globus.

Angesichts der begrenzten praktischen Größe von Globen müssen wir Karten für detaillierte Kartierungen verwenden. Karten erfordern Projektionen. Eine Projektion impliziert Verzerrung: Eine konstante Trennung auf der Karte entspricht nicht einer konstanten Trennung am Boden. Während eine Karte eine grafische Balkenskala anzeigen kann, muss die Skala mit dem Verständnis verwendet werden, dass sie nur auf einigen Linien der Karte genau ist. (Dies wird in den Beispielen in den folgenden Abschnitten weiter erläutert.)

Sei P ein Punkt bei Breitengrad φ {\displaystyle \varphi }

und Längengrad λ {\displaystyle \lambda }

auf der Kugel (oder dem Ellipsoid). Sei Q ein Nachbarpunkt und sei α {\displaystyle \alpha }

der Winkel zwischen dem Element PQ und dem Meridian bei P: Dieser Winkel ist der Azimutwinkel des Elements PQ. Seien P‘ und Q‘ entsprechende Punkte auf der Projektion. Der Winkel zwischen der Richtung P’Q‘ und der Projektion des Meridians ist die Peilung β {\displaystyle \beta }

. Im Allgemeinen α ≠ β {\displaystyle \alpha \neq \beta }

. Kommentar: diese genaue Unterscheidung zwischen Azimut (auf der Erdoberfläche) und Peilung (auf der Karte) wird nicht allgemein beobachtet, viele Autoren verwenden die Begriffe fast austauschbar. Definition: Die Punktskala bei P ist das Verhältnis der beiden Abstände P’Q‘ und PQ in der Grenze, in der sich Q P nähert. Wir schreiben dies als μ ( λ , φ , α ) = lim Q → P P ‚ Q ‚ P Q , {\displaystyle \mu (\lambda ,\,\varphi ,\,\alpha )=\lim _{Q\bis P}{\frac {P’Q‘}{PQ}},}

wobei die Notation angibt, dass die Punktskala eine Funktion der Position von P und auch der Richtung des Elements PQ ist.

Definition: wenn P und Q auf demselben Meridian liegen ( α = 0 ) {\displaystyle (\alpha =0)}

, wird die Meridianskala mit h ( λ , φ ) {\displaystyle h(\lambda ,\,\varphi )}

.

Definition: liegen P und Q auf derselben Parallele ( α = π/2 ) {\displaystyle (\alpha =\pi /2)}

, so wird die parallele Skala mit k (λ , φ ) {\displaystyle k(\lambda ,\,\varphi )}

.

Definition: wenn die Punktskala nur von der Position und nicht von der Richtung abhängt, sagen wir, dass sie isotrop ist und bezeichnen ihren Wert in jeder Richtung konventionell mit dem parallelen Skalenfaktor k ( λ , φ ) {\displaystyle k(\lambda ,\varphi )}

. Definition: Eine Kartenprojektion wird als konform bezeichnet, wenn der Winkel zwischen einem Linienpaar, das sich an einem Punkt P schneidet, derselbe ist wie der Winkel zwischen den projizierten Linien am projizierten Punkt P’für alle Linienpaare, die sich am Punkt P schneiden. Umgekehrt implizieren isotrope Skalenfaktoren über die Karte eine konforme Projektion.

Die Isotropie der Skala impliziert, dass kleine Elemente in alle Richtungen gleich gestreckt werden, dh die Form eines kleinen Elements bleibt erhalten. Dies ist die Eigenschaft des Orthomorphismus (aus dem Griechischen ‚richtige Form‘). Die Qualifizierung ‚klein‘ bedeutet, dass bei einer bestimmten Messgenauigkeit keine Änderung des Skalierungsfaktors über dem Element festgestellt werden kann. Da konforme Projektionen einen isotropen Skalenfaktor haben, wurden sie auch als orthomorphe Projektionen bezeichnet. Beispielsweise, Die Mercator-Projektion ist konform, da sie so konstruiert ist, dass Winkel erhalten bleiben, und ihr Skalierungsfaktor isotop ist, nur eine Funktion des Breitengrads: Mercator behält die Form in kleinen Regionen bei.

Definition: Auf einer konformen Projektion mit einer isotropen Skala können Punkte, die den gleichen Skalenwert haben, zu den isoskaligen Linien verbunden werden. Diese sind nicht auf Karten für Endbenutzer dargestellt, aber sie sind in vielen der Standardtexte enthalten. (Siehe Snyder Seiten 203-206.)

Der repräsentative Bruch (RF) oder die Hauptskala

Es gibt zwei Konventionen, um die Gleichungen einer gegebenen Projektion festzulegen. Zum Beispiel kann die äquirechteckige zylindrische Projektion wie folgt geschrieben werden:Kartographen: x = a λ {\displaystyle x=a\lambda }

y = a φ {\displaystyle y=a\varphi }

Mathematiker: x = λ {\displaystyle x=\lambda }

y = φ {\displaystyle y=\varphi }

Hier werden wir die erste dieser Konventionen übernehmen (nach der Verwendung in den Umfragen von Snyder). Die obigen Projektionsgleichungen definieren eindeutig Positionen auf einem riesigen Zylinder, der um die Erde gewickelt und dann abgerollt wird. Wir sagen, dass diese Koordinaten die Projektionskarte definieren, die logisch von den tatsächlich gedruckten (oder betrachteten) Karten unterschieden werden muss. Wenn die Definition der Punktskala im vorherigen Abschnitt in Bezug auf die Projektionskarte erfolgt, können wir erwarten, dass die Skalenfaktoren nahe an der Einheit liegen. Für normale tangentiale zylindrische Projektionen ist die Skala entlang des Äquators k = 1 und im Allgemeinen ändert sich die Skala, wenn wir uns vom Äquator entfernen. Die Analyse des Maßstabs auf der Projektionskarte ist eine Untersuchung der Veränderung von k weg von seinem wahren Wert der Einheit.

Tatsächliche gedruckte Karten werden aus der Projektionskarte durch eine konstante Skalierung erzeugt, die mit einem Verhältnis wie 1:100M (für ganze Weltkarten) oder 1:10000 (für Stadtpläne) bezeichnet wird. Um Verwechslungen bei der Verwendung des Wortes ‚Maßstab‘ zu vermeiden, wird dieser konstante Skalenbruchteil als repräsentativer Bruchteil (RF) der gedruckten Karte bezeichnet und ist mit dem auf der Karte gedruckten Verhältnis zu identifizieren. Die tatsächlichen gedruckten Kartenkoordinaten für die äquirektanguläre zylindrische Projektion sind

gedruckte Karte: x = ( R F ) a λ {\displaystyle x=(RF)a\lambda }

y = ( R F ) a φ {\displaystyle y=(RF)a\varphi }

rmöglicht eine klare Unterscheidung der intrinsischen Projektionsskalierung und der Reduktionsskalierung.

Ab diesem Punkt ignorieren wir die RF und arbeiten mit der Projektionskarte.

Visualisierung der Punktskala: die Tissot Indicatrix

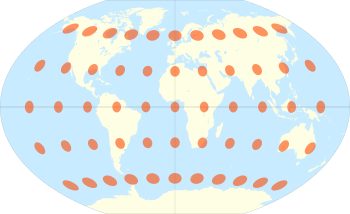
Betrachten Sie einen kleinen Kreis auf der Erdoberfläche, der an einem Punkt P auf dem Breitengrad φ {\displaystyle \varphi } zentriert ist

und Länge λ {\displaystyle \lambda }

. Da die Punktskala mit Position und Richtung variiert, wird die Projektion des Kreises auf die Projektion verzerrt. Tissot hat bewiesen, dass der Kreis auf der Projektion zu einer Ellipse wird, solange die Verzerrung nicht zu groß ist. Im Allgemeinen ändern sich die Dimension, Form und Ausrichtung der Ellipse über die Projektion. Das Überlagern dieser Verzerrungsellipsen auf die Kartenprojektion vermittelt die Art und Weise, wie sich die Punktskala über die Karte ändert. Die Verzerrungsellipse ist als Tissots Indikatrix bekannt. Das hier gezeigte Beispiel ist die Winkel-Tripel-Projektion, die Standardprojektion für Weltkarten der National Geographic Society. Die minimale Verzerrung liegt auf dem zentralen Meridian in Breitengraden von 30 Grad (Norden und Süden). (Weitere Beispiele).

Punktskala für normale zylindrische Projektionen der Kugelbearbeiten

Der Schlüssel zu einem quantitativen Verständnis der Skala besteht darin, ein infinitesimales Element auf der Kugel zu betrachten. Die Abbildung zeigt einen Punkt P bei Breitengrad φ {\displaystyle \varphi }

und Längengrad λ {\displaystyle \lambda }

auf der Kugel. Der Punkt Q liegt bei Breitengrad φ + δ φ {\displaystyle \varphi +\delta \varphi }

und Längengrad λ + δ λ {\displaystyle \lambda +\delta \lambda }

. Die Linien PK und MQ sind Bögen von Meridianen der Länge a δ φ {\displaystyle a\,\delta \varphi }

wobei a {\displaystyle a}

der Radius der Kugel und φ {\displaystyle \varphi }

ist im Bogenmaß. Die Linien PM und KQ sind Bögen paralleler Kreise der Länge (a cos ⁡ φ ) δ λ {\displaystyle (a\cos\varphi )\delta \lambda }

mit λ {\displaystyle \lambda }

in radiant Maßnahme. Um eine Punkteigenschaft der Projektion bei P abzuleiten, genügt es, ein infinitesimales Element PMQK der Oberfläche zu nehmen: In der Grenze von Q, die sich P nähert, tendiert ein solches Element zu einem infinitesimal kleinen ebenen Rechteck.

Normale zylindrische Projektionen der Kugel haben x = a λ {\displaystyle x=a\lambda }

und y {\displaystyle y}

gleich nur einer Funktion der Breite. Daher projiziert das infinitesimale Element PMQK auf der Kugel auf ein infinitesimales Element P’M’Q’K‘, das ein genaues Rechteck mit einer Basis δ x = a δ λ {\displaystyle \delta x=a\,\delta \lambda }

und einer Höhe δ y {\displaystyle \delta y}

. Durch den Vergleich der Elemente auf Kugel und Projektion können wir sofort Ausdrücke für die Skalenfaktoren auf Parallelen und Meridianen ableiten. (Die Behandlung der Skala in einer allgemeinen Richtung kann unten gefunden werden.) paralleler Skalierungsfaktor k = δ x cos ⁡ φ δ λ = sec ⁡ φ {\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}

Meridian-Skalierungsfaktor h = δ und δ φ = y ‚( φ ) a {\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}={\dfrac {y'(\varphi )}{a}}}

Beachten Sie, dass der parallele Skalierungsfaktor k = sec ⁡ φ {\displaystyle k=\sec \varphi }

die Definition von y( φ ) {\displaystyle y(\varphi )}

ist also für alle normalen zylindrischen Projektionen gleich. Es ist nützlich zu beachten, dass bei 30 Grad Breite die parallele Skala k = sec ist ⁡ 30 ∘ = 2 / 3 = 1.15 {\ displaystyle k=\sec 30^{\circ }=2/{\sqrt {3}}=1.15}

latitude 45-Grad-parallel-Skala ist k = sec ⁡ 45 ∘ = 2 = 1.414 {\displaystyle k=\sec 45^{\circ }={\sqrt {2}}=1.414}

auf dem Breitengrad 60-Grad-parallel-Skala ist k = sec ⁡ 60 ∘ = 2 {\displaystyle k=\sec 60^{\circ }=2}

latitude 80-Grad-parallel-Skala ist k = sec ⁡ 80 ∘ = 5.76 {\displaystyle k=\sec 80^{\circ }=5.76}

bei 85 Grad Breite ist die parallele Skala k = sec ⁡ 85 ∘ = 11.5 {\displaystyle k=\sec 85^{\circ }=11.5}

Die folgenden Beispiele veranschaulichen drei normale zylindrische Projektionen und in jedem Fall wird die Variation der Skala mit Position und Richtung durch die Verwendung von Tissot’s Indicatrix.

Drei Beispiele für normale zylindrische Projektionbearbeiten

Die äquidistante Projektion

Die äquirechteckige Projektion, auch bekannt als die Platte Carrée (französisch für „flaches Quadrat“) oder (etwas irreführend) die äquidistante Projektion, ist definiert durch

x = a λ , {\displaystyle x=a\lambda ,}

y = a φ , {\displaystyle y=a\varphi ,}

wobei a {\displaystyle a}

der Radius der Kugel ist, λ {\displaystyle \lambda }

der Längengrad vom zentralen Meridian der Projektion (hier als Greenwich-Meridian bei λ = 0 {\displaystyle \lambda =0}

) und φ {\displaystyle \varphi }

ist der Breitengrad. Beachten Sie, dass λ {\displaystyle \lambda }

und φ {\displaystyle \varphi }

im Bogenmaß sind (erhalten durch Multiplikation des Gradmaßes mit einem Faktor von π {\displaystyle \pi }

/180). Der Längengrad λ {\displaystyle \lambda }

liegt im Bereich {\displaystyle }

und der Breitengrad φ {\displaystyle \varphi }

liegt im Bereich {\ \displaystyle }

.

Da y ‚ (φ ) = 1 {\displaystyle y'(\varphi )=1}

Der vorherige Abschnitt gibt eine parallele Skala an, k = δ x a cos ⁡ φ δ λ = sec ⁡ φ {\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}

Meridianskala h = δ y a δ φ = 1 {\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}=\,1}

Zur Berechnung der Punktskala in beliebiger Richtung siehe Anhang.

Die Abbildung zeigt die Tissot-Indikatrix für diese Projektion. Auf dem Äquator h=k=1 und die kreisförmigen Elemente sind unverzerrt aufprojektion. In höheren Breiten werden die Kreise zu einer Ellipse verzerrt, die nur durch Dehnung in paralleler Richtung gegeben ist: Es gibt keine Verzerrung in Meridianrichtung. Das Verhältnis der Hauptachse zur Nebenachse ist sec ⁡ φ {\displaystyle \sec \varphi }

. Offensichtlich nimmt die Fläche der Ellipse um den gleichen Faktor zu.

Es ist aufschlussreich, die Verwendung von Taktskalen in Betracht zu ziehen, die auf einer gedruckten Version dieser Projektion erscheinen könnten. Die Skala ist wahr (k = 1) auf dem Äquator, so dass die Multiplikation ihrer Länge auf einer gedruckten Karte mit der Umkehrung der Skala (oder Hauptskala) den tatsächlichen Umfang der Erde ergibt. Die Balkenskala auf der Karte wird ebenfalls im wahren Maßstab gezeichnet, sodass die Übertragung eines Abstands zwischen zwei Punkten auf dem Äquator auf die Balkenskala den korrekten Abstand zwischen diesen Punkten ergibt. Das gleiche gilt für die Meridiane. Auf einer anderen Parallele als dem Äquator ist die Skala sec ⁡ φ {\displaystyle \sec \varphi }

Wenn wir also eine Trennung von einer Parallele auf die Balkenskala übertragen, müssen wir den Abstand der Balkenskala durch diesen Faktor dividieren, um den Abstand zwischen den Punkten zu erhalten, wenn wir entlang der Parallele gemessen werden (was nicht der wahre Abstand entlang eines großen Kreises ist). Auf einer Linie mit einer Peilung von beispielsweise 45 Grad ( β = 45 ∘ {\displaystyle \beta =45^{\circ }}

) ändert sich die Skala kontinuierlich mit dem Breitengrad, und die Übertragung einer Trennung entlang der Linie auf die Balkenskala gibt auf einfache Weise keinen Abstand an, der mit der wahren Entfernung zusammenhängt. (Siehe Addendum). Selbst wenn wir einen Abstand entlang dieser konstanten Peilungslinie berechnen könnten, ist seine Relevanz fraglich, da eine solche Linie auf der Projektion einer komplizierten Kurve auf der Kugel entspricht. Aus diesen Gründen müssen Balkenskalen auf kleinen Karten mit äußerster Vorsicht verwendet werden.

Mercator projectionEdit

Die Mercatorprojektion bildet die Kugel auf ein Rechteck ab (von unendlicher Ausdehnung in der y {\displaystyle y}

-Richtung) durch die Gleichungen x = a λ {\displaystyle x=a\lambda \,}

y = ein ln ⁡ {\displaystyle y=ein\ln \left}

wobei a, λ {\displaystyle \lambda \,}

und φ {\displaystyle \varphi \,}

sind wie im vorherigen Beispiel. Da y ‚(φ ) = sec ⁡ φ {\displaystyle y'(\varphi )=a\sec \varphi }

die Skalenfaktoren sind: parallele Skala k = δ x cos ⁡ φ δ λ = sec ⁡ φ . {\displaystyle k\;=\; {\dfrac {\delta x}{ein \ cos \ varphi \, \delta \lambda \,}}=\, \ sec \varphi .}

Meridianskala h = δ und a δ φ = sec ⁡ φ . {\displaystyle h\;=\; {\dfrac {\delta y} {ein\, \ delta \ varphi \,}}=\, \ sec \ varphi .}

Im mathematischen Addendum wird gezeigt, dass die Punktskala in einer beliebigen Richtung auch gleich sec ⁡ φ {\displaystyle \sec \varphi } ist

Die Skala ist also isotrop (in alle Richtungen gleich), ihre Größe nimmt mit der Breite zu als sec ⁡ φ {\displaystyle \sec \varphi }

. Im Tissot-Diagramm behält jedes infinitesimale kreisförmige Element seine Form bei, wird jedoch mit zunehmendem Breitengrad immer mehr vergrößert.

Lamberts flächengleiche Projektionbearbeiten

Lamberts flächengleiche Projektion bildet die Kugel durch die Gleichungen auf ein endliches Rechteck ab

x = ein λ y = ein sin ⁡ φ {\displaystyle x=ein\lambda \qquad \qquad y=ein\sin \varphi }

wobei a, λ {\displaystyle \lambda }

und φ {\displaystyle \varphi }

sind wie im vorherigen Beispiel. Da y ‚(φ ) = cos ⁡ φ {\displaystyle y'(\varphi )=\cos \varphi }

sind die Skalenfaktoren Parallelskala k = δ x cos ⁡ φ δ λ = sec ⁡ φ {\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}

Meridianskala h = δy a δ φ = cos ⁡ φ {\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}=\,\cos \varphi }

Die Berechnung der Punktskala in einer beliebigen Richtung ist unten angegeben.

Die vertikalen und horizontalen Skalen kompensieren sich nun gegenseitig (hk=1) und im Tissot-Diagramm wird jedes infinitesimale kreisförmige Element zu einer Ellipse verzerrt, die dieselbe Fläche wie die unverzerrten Kreise auf dem Äquator hat.

Graphen von Skalenfaktorenbearbeiten

Die Grafik zeigt die Variation der Skalierungsfaktoren für die obigen drei Beispiele. Das obere Diagramm zeigt die isotrope Mercator-Skalenfunktion: Die Skala auf der Parallele ist dieselbe wie die Skala auf dem Meridian. Die anderen Diagramme zeigen den Meridianskalierungsfaktor für die äquirektanguläre Projektion (h = 1) und für die Lambert-flächengleiche Projektion. Diese letzten beiden Projektionen haben eine parallele Skala, die mit der des Mercator-Plots identisch ist. Für die Lambert beachten Sie, dass die parallele Skala (als Mercator A) mit dem Breitengrad zunimmt und die Meridianskala (C) mit dem Breitengrad abnimmt, so dass hk = 1 ist, was die Flächenerhaltung garantiert.

Skalenvariation der Mercator-Projektion

Die Mercator-Punktskala wird auf dem Äquator verwendet, da der bei seiner Konstruktion verwendete Hilfszylinder tangential zur Erde am Äquator ist. Aus diesem Grund sollte die übliche Projektion als Tangentenprojektion bezeichnet werden. Die Skala variiert mit dem Breitengrad als k = sec ⁡ φ {\displaystyle k=\sec \varphi }

. Da sec ⁡ φ {\displaystyle \sec \varphi }

bei Annäherung an die Pole gegen unendlich tendiert, ist die Mercatorkarte in hohen Breitengraden stark verzerrt und aus diesem Grund ist die Projektion für Weltkarten völlig ungeeignet (es sei denn, wir diskutieren Navigation und Loxodromen). Bei einem Breitengrad von etwa 25 Grad beträgt der Wert von sec ⁡ φ {\displaystyle \sec \varphi }

jedoch etwa 1.1 Mercator ist also in einem Streifen der Breite von 50 Grad, der auf dem Äquator zentriert ist, auf 10% genau. Schmalere Streifen sind besser: Ein Streifen mit einer Breite von 16 Grad (zentriert auf dem Äquator) ist auf 1% oder 1 Teil von 100 genau.

Ein Standardkriterium für gute großformatige Karten ist, dass die Genauigkeit innerhalb von 4 Teilen in 10.000 oder 0,04% liegen sollte, entsprechend k = 1,0004 {\displaystyle k=1,0004}

. Da sec ⁡ φ {\displaystyle \sec \varphi }

diesen Wert bei φ = 1 erreicht.62 {\displaystyle \varphi =1.62}

Grad (siehe Abbildung unten, rote Linie). Daher ist die tangentiale Mercatorprojektion innerhalb eines Streifens mit einer Breite von 3,24 Grad, der auf dem Äquator zentriert ist, sehr genau. Dies entspricht einer Nord-Süd-Entfernung von etwa 360 km (220 mi). Innerhalb dieses Streifens ist Mercator sehr gut, sehr genau und formerhaltend, weil es konform ist (winkelerhaltend). Diese Beobachtungen veranlassten die Entwicklung der transversalen Mercator-Projektionen, bei denen ein Meridian wie ein Äquator der Projektion behandelt wird, so dass wir eine genaue Karte in einem engen Abstand von diesem Meridian erhalten. Solche Karten sind gut für Länder, die fast nord-Süd ausgerichtet sind (wie Großbritannien), und ein Satz von 60 solcher Karten wird für den Universal Transverse Mercator (UTM) verwendet. Beachten Sie, dass in diesen beiden Projektionen (die auf verschiedenen Ellipsoiden basieren) die Transformationsgleichungen für x und y und der Ausdruck für den Skalierungsfaktor komplizierte Funktionen sowohl der Breite als auch der Länge sind.

Sekante oder modifizierte Projektionenbearbeiten

Die Grundidee einer Sekantenprojektion ist, dass die Kugel auf einen Zylinder projiziert wird, der die Kugel an zwei Parallelen schneidet, sagen wir φ 1 {\displaystyle \varphi _{1}}

Nord und Süd. Offensichtlich ist die Skala jetzt in diesen Breiten wahr, während Parallelen unterhalb dieser Breiten durch die Projektion kontrahiert werden und ihr (paralleler) Skalierungsfaktor kleiner als eins sein muss. Das Ergebnis ist, dass die Abweichung der Skala von der Einheit über einen größeren Breitenbereich reduziert wird.

Als Beispiel ist eine mögliche Sekanten-Mercator-Projektion definiert durch

x = 0,9996 a λ y = 0,9996 a ln ⁡ (tan ⁡ (π 4 + φ 2) ) . {\displaystyle x=0,9996a\lambda \qquad \qquad y=0,9996a\ln \links(\tan \links({\frac {\pi }{4}}+{\frac {\varphi }{2}}\rechts)\rechts).}

Die numerischen Multiplikatoren ändern die Form der Projektion nicht, aber es bedeutet, dass die Skalenfaktoren geändert werden:

Sekante Mercatorskala, k = 0,9996 sec ⁡ φ . {\displaystyle \quad k\;=0,9996\sec \varphi .}

Somit

• die Skala am Äquator ist 0,9996,
• die Skala ist k = 1 bei einem Breitengrad gegeben durch φ 1 {\displaystyle \varphi _{1}}
  

  wobei sec ⁡ φ 1 = 1 / 0,9996 = 1,00004 {\displaystyle \sek \varphi} _{1}=1/0.9996=1.00004}

  

  so dass φ 1 = 1,62 {\displaystyle \varphi _{1}=1,62}

  

  Grad, k=1,0004 auf dem Breitengrad φ 2 {\displaystyle \varphi _{2}}

  

  gegeben durch die sec ⁡ φ 2 = 1,0004 / 0,9996 = 1,0008 {\displaystyle \sec \varphi _{2}=1.0004/0.9996=1.0008}

  

  für die φ 2 = 2,29 Unterstützung {\displaystyle \varphi _{2}=2 hat.29}

  

  Grad. Daher hat die Projektion 1 < k < 1.0004 {\displaystyle 1<k<1.0004}

  

  , das ist eine Genauigkeit von 0,04% über einen breiteren Streifen von 4,58 Grad (verglichen mit 3,24 Grad für die Tangentenform).

Dies wird durch die untere (grüne) Kurve in der Abbildung des vorherigen Abschnitts veranschaulicht.

Solche schmalen Zonen von hoher Genauigkeit werden in der UTM- und der britischen OSGB-Projektion verwendet, die beide sekante, transversale Mercator auf dem Ellipsoid mit der Skala auf der zentralen Meridiankonstante bei k 0 = 0,9996 {\displaystyle k_{0}=0,9996} sind

. Die isoskaligen Linien mit k = 1 {\displaystyle k=1}

sind leicht gekrümmte Linien etwa 180 km östlich und westlich des Zentralmeridians. Der Maximalwert des Skalierungsfaktors beträgt 1,001 für UTM und 1,0007 für OSGB.

Die Maßeinheitslinien auf dem Breitengrad φ 1 {\displaystyle \varphi _{1}}

(Nord und Süd), wo die zylindrische Projektionsfläche die Kugel schneidet, sind die Standardparallelen der Sekantenprojektion.

Ist ein schmales Band mit | k – 1 / < 0.0004 {\displaystyle |k-1/<0.0004}

ist wichtig für hochgenaue Kartierungen in großem Maßstab, für Weltkarten werden viel breiter beabstandete Standardparallelen verwendet, um die Skalenvariation zu steuern. Beispiele sind

• Behrmann mit Standardparallelen bei 30N, 30S.
• Gall equal area mit Standardparallelen bei 45N, 45S.

Die Skalendiagramme für letztere sind unten im Vergleich zu den Lambert Equal Area Skalenfaktoren dargestellt. In letzterem ist der Äquator eine einzige Standardparallele und die parallele Skala nimmt von k = 1 zu, um die Abnahme der Meridianskala auszugleichen. Für die Galle wird die Parallelskala am Äquator reduziert (auf k = 0,707), während die Meridianskala erhöht wird (auf k = 1,414). Dies führt zu der groben Verzerrung der Form in der Gallpetersschen Projektion. (Auf dem Globus ist Afrika ungefähr so lang wie breit). Beachten Sie, dass die Meridian- und Parallelskalen beide auf den Standardparallelen basieren.

Mathematisches addendumEdit

Für normale zylindrische Projektionen ergibt die Geometrie der infinitesimalen Elemente

(a) tan ⁡ α = ein cos ⁡ φ δ λ ein δ φ , {\displaystyle {\text{(a)}}\quad \tan \alpha ={\frac {a\cos \varphi \,\delta \lambda }{a\,\delta \varphi }},}

(b) tan ⁡ β = δ x δ y = a δ λ δ y. {\displaystyle {\text{(b)}}\quad \tan \beta ={\frac {\delta x}{\delta y}}={\frac {a\,\delta \lambda }{\delta y}}.}