Definition phylogenetischer Netzwerke
Wir folgen der Definition der phylogenetischen Netzwerke gemäß Definition 4, Seite 16]. Für alle anderen graphentheoretischen Definitionen, die hier nicht gegeben sind, folgen wir . Ein verwurzeltes phylogenetisches Netzwerk, hier einfach als phylogenetisches Netzwerk bezeichnet, ist definiert als ein verwurzelter, gerichteter azyklischer Graph (DAG), dessen Wurzel indegree 0 und die Blätter outdegree 0 . Die Scheitelpunkte, deren Indegree größer als 1 sind, werden als retikuläre Scheitelpunkte bezeichnet, und die Kanten mit retikulären Scheitelpunkten als Kopfscheitelpunkte werden als retikuläre Kanten bezeichnet. Alle anderen Kanten werden als Baumkanten bezeichnet. Die in gegebene Definition kümmert sich um die sogenannte „Zeitkonsistenz“ -Einschränkung, nämlich dass die Baumkanten in einer positiven Zeit stattfinden und die netzartigen Eckpunkte Eltern haben, die nur „zeitlich koexistieren“ können. Daher, vorwärts, Wir erinnern uns an die formale Definition von phylogenetischen Netzwerken wie in gegeben .
Bei jedem gerichteten Graphen sagen wir, dass zwei Eckpunkte u und v zeitlich nicht koexistieren können, wenn eine Sequenz P = (p1, p2, …, p k) von Pfaden in N, so dass:
-
p i ein gerichteter Pfad ist, der mindestens eine Baumkante enthält, für jede 1 ≤ i ≤ k,
-
u ist der Schwanz von p 1, und v ist der Kopf von p k , und
-
für jede 1 ≤ i ≤ k – 1 gibt es einen Netzwerkscheitelpunkt, dessen zwei Elternteile der Kopf p i und der Schwanz von p i+ 1 sind.
Ein phylogenetisches Netzwerk N ist eine verwurzelte DAG, die den folgenden Einschränkungen unterliegt:
-
Jeder Vertex hat indegree und outdegree definiert durch eine der vier Kombinationen (0, 2), (1, 0), (1, 2), oder (2, 1) – entsprechend Wurzel, Blättern, inneren Baumscheitelpunkten und netzförmigen Scheitelpunkten. Alle anderen Scheitelpunkte als netzförmige Scheitelpunkte werden als Baumscheitelpunkte bezeichnet.
-
Wenn zwei Scheitelpunkte u und v zeitlich nicht koexistieren können, gibt es keinen Netzwerkscheitelpunkt w mit Kanten (u, w) und (v, w).
-
Bei jeder Kante des Netzwerks muss mindestens einer seiner Endpunkte ein Baumscheitelpunkt sein.
Eine weitere Komponente dieser Definition ist, dass für jede Kante im phylogenetischen Netzwerk mindestens einer ihrer Endpunkte (entweder der Kopf oder der Schwanz) ein Baumscheitelpunkt ist. Hier werden wir diese Definition verwenden. Wo immer möglich, weisen wir darauf hin, ob die Bedingungen der Definition notwendig sind.
Phylogenetische Netzwerke können naïvely als ein Netzwerk betrachtet werden, das als Subgraphen die Bäume enthält, die die Evolutionsgeschichten verschiedener Segmente der Eingangsterminalsequenzen erklären. Bei einem phylogenetischen Netzwerk garantiert das Löschen einer jeden Kante, die auf einen netzförmigen Scheitelpunkt trifft, keinen resultierenden phylogenetischen Baum mit demselben Satz von Blättern wie der des Netzwerks. Dies ist eine unerwünschte Eigenschaft, insbesondere wenn das Sparsamkeitskriterium definiert wird, indem ein phylogenetischer Baum innerhalb des Netzwerks gefunden wird, der für den angegebenen Standort am sparsamsten ist, wie in definiert . Um dieses Problem zu vermeiden, muss davon ausgegangen werden, dass kein interner Scheitelpunkt zwei retikuläre Kinder hat. Wir nennen diese Klasse von phylogenetischen Netzwerken als phylogenetisches Netzwerk ohne Schwesterretikulationen. Siehe Abbildung 1 für einige Beispiele phylogenetischer Netzwerke.
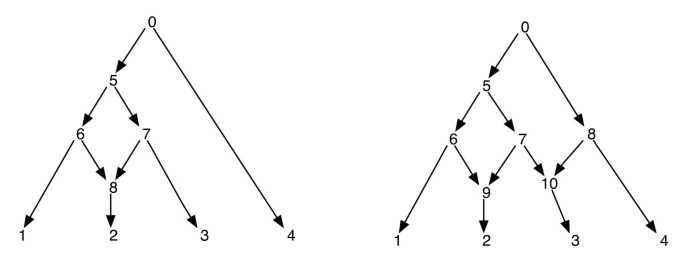
Phylogenetische Netzwerke. Die Abbildung zeigt zwei phylogenetische Netzwerke; Das linke hat nur einen einzigen netzartigen Scheitelpunkt und das rechte hat zwei netzartige Scheitelpunkte, die nahe beieinander liegen. Beachten Sie, dass das Entfernen der Kanten (7, 9) und (7, 10) aus dem Netzwerk rechts nicht zu einem Baum führt, in dem der Scheitelpunkt 7 ein Blatt ist. Dies zeigt, dass das Entfernen einer eingehenden Kante pro netzförmigem Scheitelpunkt nicht unbedingt einen Baum mit demselben Blattsatz wie das Netzwerk erzeugt. Die Nachbestellung und die Vorbestellung der Eckpunkte des Netzwerks auf der linken Seite sind 1, 2, 8, 6, 3, 7, 5, 4, 0 und 0, 5, 6, 1, 8, 2, 7, 3, 4 jeweils und für das Netzwerk auf der rechten Seite sind sie 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 und 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 beziehungsweise.
Bevor wir mit der Definition der Sparsamkeitsprobleme fortfahren, ist das Folgende eine nützliche Beobachtung. Für ein phylogenetisches Netzwerk N ohne Schwesterretikulationen und mit r retikulären Scheitelpunkten und mit Blattmenge X bezeichnen wir T (N) als die Menge aller in N enthaltenen Bäume. Jeder solche Baum wird durch die folgenden zwei Schritte erhalten: (1) Entfernen Sie für jeden retikulären Scheitelpunkt eine der eingehenden Kanten, und ziehen Sie dann (2) für jeden Scheitelpunkt v von indegree und outdegree 1, dessen Elternteil u und Kind w ist, die Kanten (u, v) und (v, w). Die Bedingung, dass jede Kante in N einen Baumscheitelpunkt als Endpunkt hat und dass jeder Baumscheitelpunkt mindestens einen Baumscheitelpunkt als untergeordnetes Element hat, stellt sicher, dass die Menge der Blätter des resultierenden Baums mit der des Netzwerks übereinstimmt. Daher enthält die Menge T ( N ) genau 2rphylogenetische Bäume, deren Blattmenge genau X.
Maximale Sparsamkeit
Wir verweisen die Leser auf eine allgemeine Beschreibung der Idee der Sparsamkeit und auf die Diskussion verschiedener Sparsamkeitsalgorithmen. Es wurde darauf hingewiesen, dass die Sparsamkeitsmethode für Bäume auf phylogenetische Netzwerke ausgedehnt werden kann. In einer Reihe von Arbeiten , Ein solches Sparsamkeitskriterium wird definiert, indem ein Baum im Netzwerk gefunden wird, der die beste sparsame Punktzahl aufweist, und effiziente Algorithmen zur Optimierung dieses Kriteriums für ein bestimmtes phylogenetisches Netzwerk wurden entwickelt. Obwohl gezeigt wird, dass diese Algorithmen in der Praxis gut funktionieren, können sie nur für phylogenetische Netzwerke ohne Schwesterretikulationen korrekt funktionieren, da es einfach ist, in dieser eingeschränkten Klasse von Netzwerken nach einem optimalen Baum zu suchen. In diesem Abschnitt, Wir geben eine alternative Version des Sparsamkeitsproblems an und stellen in den folgenden Abschnitten einige heuristische Lösungen zur Optimierung der Punktzahl in jedem phylogenetischen Netzwerk bereit.
Sei = {1, 2, …, n} bezeichnen die Menge der Blattbezeichnungen eines gegebenen phylogenetischen Netzwerks N. Eine Funktion λ: → {0, 1, …,/Σ/ – 1} wird eine Zustandszuweisungsfunktion über das Alphabet Σ (eine nicht leere Menge) für N. Wir sagen, dass eine Funktion λ ^ :V ( N ) → { 0 , 1 , … , | Σ / – 1 } ist eine Erweiterung von λ auf N, wenn sie mit λ auf den Blättern von N übereinstimmt. Für einen Scheitelpunkt v in N nennen wir λ ^ ( v ) als Zuweisung von λ ^ auf v. Ein vollständig zugewiesenes Netzwerk ist ein Netzwerk, in dem alle Scheitelpunkte Beschriftungen von {0, 1, …, |Σ| – 1}. Sei C eine Kostenmatrix, deren ij-Eintrag c ij die Kosten für die Transformation von Zustand i in Zustand j entlang einer beliebigen Kante in N sind. Wenn e = (u, v) eine Kante in N ist, wobei u das übergeordnete Element von v ist, bezeichnen wir w e (λ ) ^ = c i j , wobei i = λ ^ (u) und j= λ ^ (v) . Für einen Graphen G bezeichnen wir E(G) die Kantenmenge von G. Dann ist das Sparsamkeitsproblem wie folgt definiert.
Eingabe: Ein phylogenetisches Netzwerk N mit Blattbezeichnungen und einer Zustandszuordnungsfunktion λ über dem Alphabet Σ für N.
Sparsamkeitskriterium: Für eine Erweiterung λ^ von λ sei
und
Ausgabe: Suchen Sie bei P ∈ {P1, P2} λ ^ , das P ( λ ^ ) minimiert.
Wir stellen fest, dass P 1 ( λ ^ ) in eingeführt wird und P 2 ( λ ^ ) die Definition ist, die wir in diesem Artikel verwenden werden. Ein allgemeinerer Ansatz besteht darin, Q ( λ ^ ) = ∑ e ∈ E ( N ) d e (w e (λ ^ ) ) zu minimieren , wobei d e eine nicht negative Gewichtsfunktion an den Rändern von N. Für die Zwecke dieses Artikels beschränken wir uns auf P = P2, obwohl der erste unserer Ansätze, die dynamische Programmierlösung, auch für P = Q gilt.
Sparsamkeitsalgorithmen in Netzwerken
Durchlaufen eines phylogenetischen Netzwerks
In einem Netzwerk traversal bezieht sich auf den Prozess des systematischen Besuchs jedes Scheitelpunkts genau einmal. Solche Traversen werden nach der Reihenfolge klassifiziert, in der die Scheitelpunkte besucht werden. Wir benötigen zwei Arten von Netzwerk-Vertex-Traversals, um unsere Algorithmen zu beschreiben. Diese sind bekannt für phylogenetische Bäume, und wir präsentieren sie hier für phylogenetische Netzwerke. Die unten angegebenen Algorithmen für die Traversen gehen von einem beliebigen Scheitelpunkt v im Netzwerk aus. In diesem Artikel werden wir die Traversen immer vom Wurzelscheitelpunkt des Netzwerks aus durchführen.
Pre-Order-Traversal eines phylogenetischen Netzwerks von einem Scheitelpunkt v
-
Besuchen Sie den Scheitelpunkt v.
-
Führen Sie rekursiv Pre-Order-Traversal von jedem Kind durch, das noch nicht besucht wurde.
Post-Order-Traversal eines phylogenetischen Netzwerks von einem Scheitelpunkt v
-
Führen Sie rekursiv Post-Order-Traversal von jedem Kind durch, das noch nicht besucht wurde.
-
Besuchen Sie den Scheitelpunkt v.
Da ein phylogenetisches Netzwerk eine DAG ist, besuchen solche Traversen alle Scheitelpunkte des Netzwerks genau einmal. (Weitere Informationen zur Existenz solcher Traversen auf DAGs finden Sie unter). Für die Zwecke dieses Artikels gehen wir davon aus, dass die Eckpunkte eines Netzwerks eindeutig durch Ganzzahlen gekennzeichnet sind. Beachten Sie, dass die Blätter bereits aus dem Set beschriftet sind ; und so verwenden wir andere ganze Zahlen für andere Eckpunkte. Wann immer die untergeordneten Eckpunkte von v extrahiert werden, werden sie auch in aufsteigender Reihenfolge ihrer ganzzahligen Beschriftungen angeordnet, und die Vor- und Nachordnungsdurchläufe werden in dieser Reihenfolge durchgeführt. Dadurch wird Folgendes sichergestellt: Wenn die Scheitelpunkte v und v‘ so sind, dass kein gerichteter Pfad zwischen ihnen besteht, wird der Scheitelpunkt v vor dem Scheitelpunkt v‘ in der Vorreihenfolge genau dann durchlaufen, wenn der Scheitelpunkt v vor dem Scheitelpunkt v’in der Nachreihenfolge durchlaufen wird. Einige Beispiele finden Sie in Abbildung 1. Mit dieser Eigenschaft stellen wir fest, dass die Vor- und Nachordnungsdurchläufe von der Wurzel eines phylogenetischen Netzwerks jeweils denselben Spannbaum verfolgen, den wir hier den Traversenbaum nennen.
Dynamische Programmierlösung
Die dynamische Programmierung wird verwendet, um effiziente Lösungen zum Ermitteln des genauen Parsimony-Scores bereitzustellen, wenn das Netzwerk ein phylogenetischer Baum ist . In diesem Abschnitt zeigen wir, dass der gleiche Ansatz auf phylogenetische Netzwerke verallgemeinert werden kann. Der Sankoff-Algorithmus für einen Baum durchläuft die Scheitelpunkte des Baumes über die Nachbestellung, während er die Mindestkosten jedes Zustands an jedem Scheitelpunkt von den Blättern zur Wurzel berechnet, und wählt dann die besten Zuweisungen für jeden Scheitelpunkt aus, indem er von der Wurzel zu den Blättern zurückverfolgt, indem er die Baumscheitelpunkte über die Vorbestellung durchläuft. Beide Phasen sind für Netzwerke in Algorithmen 1 bzw. 2 dargestellt. Wir beschreiben sie unten kurz. Es kann festgestellt werden, dass, wenn das Netzwerk ein Baum ist, unsere Algorithmen mit den Vorbestellungs- und Nachbestellungsphasen der Sankoff-Methode für Bäume übereinstimmen.
Weisen Sie bei einem phylogenetischen Netzwerk N mit markierten Blattscheitelpunkten und mit Zustandszuordnungsfunktion λ über dem Alphabet Σ jedem Scheitelpunkt v ∈ V eine Größe S v (i) für jedes i ∈ Σ zu. In phylogenetischen Bäumen bezeichnet S v (i) die minimale Summe der Kosten aller Ereignisse vom Scheitelpunkt v bis zu allen Blättern, die von v aus erreichbar sind, vorausgesetzt, dass v der Zustand i zugewiesen ist und allen nachkommenden Scheitelpunkten von v jeweils ein Zustand zugewiesen ist. In Netzwerken gibt es keine einfache Möglichkeit, eine solche Menge zu berechnen. Stattdessen erlauben wir, dass SV (i) eine Untergrenze der obigen genauen Punktzahl ist und während der Nachbestellungsphase berechnet wird.
Traversal-Phase nach der Ordnung: Wenn v ein Blatt von N ist, wird S v (i) 0 zugewiesen, wenn der beobachtete Zustand Zustand i ist, und andernfalls unendlich. Jetzt brauchen wir nur noch eine Rekursionsbeziehung, um Sv (i) für den Rest der Scheitelpunkte zu berechnen. Für jedes Kind w von v sagen wir, w erfüllt die Nachbestellungs-Traversal-Bedingung in Bezug auf v oder einfach die Traversal-Bedingung in Bezug auf v im Hinblick auf die Beobachtung am Anfang dieses Abschnitts, wenn Folgendes zutrifft:
- (i)
Der Scheitelpunkt w ist ein retikulärer Scheitelpunkt und
- (ii)
Wenn v‘ das übergeordnete Element von w außer v ist, muss der Scheitelpunkt v vor v‘ in der Nachfolge durchlaufen werden Durchquerung von N.
Wir definieren jetzt rekursiv für jede Kante (v, w),
Für einen phylogenetischen Baum nimmt s(v, w)(i) immer die erste dieser Größen an und gibt somit die Summe der Substitutionskosten entlang der Kanten des Baumes an, die unterhalb des Scheitelpunkts v liegen, vorausgesetzt, dem Scheitelpunkt v ist der Zustand i zugewiesen. Um für phylogenetische Netzwerke die Substitutionskosten entlang der Kanten zu berücksichtigen, die unterhalb eines netzförmigen Scheitelpunkts w nur ein einziges Mal liegen, wenn dem Scheitelpunkt v der Zustand i zugewiesen baum berücksichtigt alle Substitutionskosten entlang aller Kanten, die unter v liegen. Wenn v andererseits kein übergeordnetes Element von w im Traversenbaum ist, bezeichnet s(v, w) (i) einfach die Substitutionskosten von Zustand i am Scheitelpunkt v in einen anderen Zustand bei w, der am wenigsten teuer ist.
Wir definieren dann
wobei die Summe für alle child(ren) vertex(s) w von v . Wie bereits erwähnt, bezeichnet S v (i) in phylogenetischen Bäumen die minimal mögliche Summe der Substitutionskosten entlang aller Kanten vom Scheitelpunkt v bis zu allen Blättern, die von v aus erreichbar sind, vorausgesetzt, dass v der Zustand i zugewiesen ist und allen von v aus erreichbaren Scheitelpunkten jeweils ein Zustand zugewiesen ist.
In phylogenetischen Netzwerken gibt es bei der Berechnung von s(v, w)(i), wobei w ein netzförmiger Scheitelpunkt ist, so dass (v, w) keine Kante im Traversenbaum ist, keine vorherige Kenntnis des Zustands, der später am netzförmigen Scheitelpunkt w zugewiesen wird. Somit kann s(v, w) (i) nur eine untere Grenze der Kanten des Netzwerks sein, die unterhalb des Scheitelpunkts v liegen, wenn dem Scheitelpunkt v der Zustand i zugewiesen ist. Die Begründung dafür ist, dass s(v, w) (i) die Substitutionskosten von Zustand i am Scheitelpunkt v zu einem anderen Zustand bei w sind, der am wenigsten teuer ist, anstelle der Substitutionskosten von Zustand i bei v zu dem Zustand bei w, der später zugewiesen wird. Da die Definition von S v (i) von der Definition von s(v, w)(i) abhängt und sie rekursiv definiert sind, beobachten wir Folgendes: S v (i) ist eine untere Grenze für die Summe der Substitutionskosten entlang der Ränder des Netzwerks, die vom Scheitelpunkt v aus erreichbar sind, vorausgesetzt, dass v der Zustand i zugewiesen ist und allen nachgeordneten Baumscheitelpunkten ein eindeutiger Zustand zugewiesen ist und den netzförmigen Scheitelpunkten zwei Zustände zugewiesen sind, die nicht unbedingt gleich sind. Die zugewiesenen Zustände des netzförmigen Scheitelpunkts tragen zu einem Konflikt bei, wenn die Zustände nicht identisch sind. Nehmen wir an, dass dem Wurzelscheitelpunkt r der Zustand i zugewiesen ist und allen Baumscheitelpunkten ein eindeutiger Zustand zugewiesen ist, während den netzförmigen Scheitelpunkten zwei Zustände zugewiesen sind. Dann bezeichnen die Kosten S r (i) die minimal mögliche Summe der Substitutionskosten entlang aller Kanten eines Traversenbaums mit einem der für retikuläre Eckpunkte zugewiesenen Zustände plus die Summe der Substitutionskosten entlang der verbleibenden retikulären Kanten mit dem alternativen Zuordnungszustand an den retikulären Eckpunkten. Da wir eine Zuweisung an den Scheitelpunkten des Netzwerks ohne Konflikte in den netzförmigen Scheitelpunkten suchen, ist S r (i) eine untere Grenze für die Kosten einer solchen Zuweisung, wobei dem Wurzelscheitelpunkt i zugewiesen wird und allen Scheitelpunkten eine eindeutige Zuweisung zugewiesen wird.
Während dieser Phase speichern wir auch die Zustände
um den Zustand von w zurückverfolgen zu können, der die Menge s(v, w)(i) während der Vorbestellungsphase erreicht. Siehe Algorithmus 1.
Traversal-Phase vorbestellen: Wir wählen zuerst das Minimum
wobei r der Wurzelscheitelpunkt ist und weisen den Zustand zu, der das Minimum am Wurzelscheitelpunkt erreicht, d.h., sei λ ^ ( r ) = i r , so dass S r (i r ) = S. Für jeden anderen Scheitelpunkt w, der kein retikulärer Scheitelpunkt ist, dessen übergeordnetem v bereits ein Zustand i zugewiesen ist, weisen wir den Zustand t(v, w) (i) zu. Für einen retikulären Scheitelpunkt w, dessen übergeordnete Scheitelpunkte v und v‘ sind, nehmen wir an, dass v und v‘ beim Durchlaufen durch die Vorreihenfolge die Zustände i bzw. Die möglichen Zustände j = t(v, w)(i) und j’= t(v‘, w)(i‘) von w, die s(v, w)(i) bzw. s(v‘, w)(i‘) erreichen, müssen nicht gleich sein. Mit anderen Worten, es ist möglich, dass j ≠ j‘. In diesem Fall haben wir einen Konflikt auf dem retikulären Scheitelpunkt w. Daher gibt die dynamische Programmiertechnik keine Erweiterung für λ an, deren Sparsamkeitswert S. In diesem Fall wählen wir einfach zwischen j und j’für λ (w), je nachdem, welcher der Scheitelpunkte unter v und v‘ zuerst in der Vorreihenfolge durchlaufen wird. Wenn also der Scheitelpunkt w die Traversierbedingung in Bezug auf v erfüllt, haben wir λ ^ ( w ) =j.
Nach Abschluss der Vorbestellungsphase können wir die Punktzahl erhalten, die der Erweiterung λ ^ entspricht, indem wir zuerst S’= S und S‘ an jedem retikulären Scheitelpunkt w wie folgt aktualisieren: Der obere Grenzwert S‘ wird entsprechend der Zuordnung j am Scheitelpunkt w als S‘-c i’j‘ +c i’j aktualisiert. Siehe Algorithmus 2. Abbildung 2 zeigt ein Beispiel für die Ausführung des Algorithmus in einem Netzwerk. Da S r (i) eine untere Grenze für die optimale Zuweisung ist, wobei der Wurzelscheitelpunkt i zugewiesen ist und allen Scheitelpunkten eine eindeutige Zuweisung zugewiesen ist, und da S = min i s r (i) , schließen wir daraus, dass S eine untere Grenze des Optimums ist, das wir suchen. Siehe Lemma 1 für einen formellen Beweis.

Dynamische Programmierlösung. Die dynamische Programmierlösung für ein phylogenetisches Netzwerk. Die Zustände sind 0, 1 und 2. Die verwendete Kostenmatrix hat alle 1s mit Ausnahme der diagonalen Elemente, die alle 0s sind. Die auf jedem Scheitelpunkt v gezeigten Tabellen sind die Kosten, S v (i) (zweite Zeile) jedes Zustands, i (erste Zeile), die während der Nachbestellung berechnet werden. An den Scheitelpunkten sind auch die Zustände des Kindes w dargestellt, nämlich die t (v, w) (i) (dritte Zeile), die den Einträgen in der zweiten Zeile entsprechen; Wenn es zwei Kinder für einen Scheitelpunkt gibt, werden die Einträge in der dritten Zeile als ein Paar von Zuständen des linken Kindes bzw. des rechten Kindes dargestellt. Jede Kante (v, w) ist für jeden Zustand i mit s(v, w)(i) gekennzeichnet. Die am Wurzelscheitelpunkt fett hervorgehobenen Kosten von 2 ergeben eine untere Grenze, S. Der an jedem Scheitelpunkt zugewiesene Zustand ist fett hervorgehoben. Der Algorithmus findet insgesamt drei Substitutionen (hervorgehoben durch fette Kanten). Dies liegt daran, dass die an den übergeordneten Scheitelpunkten des netzförmigen Scheitelpunkts zugewiesenen Zustände widersprüchliche Zuweisungen von 1 bzw. 2 ergeben, von denen der Zustand 1 am netzförmigen Scheitelpunkt zugewiesen ist. Mit zusätzlichen Kosten von 1 erhalten wir also die Punktzahl 3 (eine Obergrenze der optimalen Punktzahl) als Sparsamkeitsbewertung, die der gezeigten Aufgabe entspricht. Beachten Sie, dass der optimale Sparsamkeitswert im Netzwerk 2 ist (gleich der unteren Grenze), der durch erschöpfende Suche gefunden werden kann und durch Ändern der Zuordnung von 1 zu 2 für das linke übergeordnete Element des retikulären Scheitelpunkts und von 1 zu 2 für den retikulären Scheitelpunkt realisiert werden kann. Somit stimmt die Untergrenze mit der optimalen Punktzahl überein, obwohl die der Untergrenze entsprechende Zuordnung nicht konfliktfrei ist und nicht mit der dem Optimum entsprechenden Zuordnung übereinstimmt.
Lemma 1. Die Menge S ist eine Untergrenze des optimalen Parsimony-Scores im Netzwerk N.
Beweis. Durch die Konstruktion von S haben wir
wobei der zweite Summand für den retikulären Scheitelpunkt w ist, dessen Eltern v und v‘ sind, so dass v die Durchlaufbedingung erfüllt w.r.t . w. Somit sind die Kosten c λ ^ (v), λ ^ (w) die Substitutionskosten vom zugeordneten Zustand λ ^ (v) bei v zum Zustand λ ^ (w) bei w. Andererseits sind die Kosten c λ ^ (v ‚), t (v ‚, w) (λ ^ (v ‚)) die Substitutionskosten vom zugewiesenen Zustand λ ^ (v) bei v zum Zustand t (v ‚, w) (λ ^ (v ‚)) bei w. Beachten Sie, dass der Zustand t (v‘, w) (λ ^ (v ‚)) nicht unbedingt mit dem Zustand λ ^ (w) identisch ist und S das Minimum unter allen Zuweisungen ist, die zu Konflikten an den netzartigen Scheitelpunkten führen können.
Angenommen, S ^ ist der optimale Sparsamkeitswert für N mit der Funktion μ: V (N) → {0, 1, …, /Σ/ – 1} als Erweiterung von λ haben wir
wobei im zweiten Summanden w ist ein netzförmiger Scheitelpunkt mit Eltern v und v‘. Da μ eine konfliktfreie Zuordnung ist, die in der Menge aller Zuweisungen enthalten ist, unter deren Kosten S das Minimum ist (vergleiche Gleichung (3) und (4)), haben wir S≤ S ^ . □
Nun zur Komplexität des Algorithmus. Angenommen, das Netzwerk N hat n Blätter und r netzartige Scheitelpunkte. Dann ist die Anzahl der Eckpunkte in N 2 (n + r) -1. An jedem Scheitelpunkt v und für jeden Zustand i kann die Größe S in O(k2)-Zeit berechnet werden, wobei k = |Σ| ist. Der Schritt zum Durchlaufen vor der Bestellung besteht darin, S in O (k) -Komplexität zu finden und die besten Zustände für jeden Scheitelpunkt zuzuweisen. Das Fixieren widersprüchlicher retikulärer Scheitelpunktzustände nimmt auch O (r) Zeit in Anspruch. Daher ist die Komplexität des Algorithmus (hier vorgestellt ), um eine untere und eine obere Grenze zu finden, O((n + r) k2). Eine alternative obere Grenze kann in O (nk2) erhalten werden, indem einfach während der Nachbestellungs-Traversal-Phase für jeden retikulären Scheitelpunkt der Zustand zugewiesen wird, der die maximale Anzahl von Malen an den Blättern auftritt, die von dem jeweiligen retikulären Scheitelpunkt aus erreichbar sind; und Fortfahren über das Finden von S v (i) für die verbleibenden Scheitelpunkte. Das genaue Optimum kann auch erhalten werden, indem die möglichen Zustände auf einen einzelnen Zustand für jeden retikulären Scheitelpunkt beschränkt werden, indem der dynamische Programmieralgorithmus für jede der kr-Kombinationen von Zuständen für die retikulären Scheitelpunkte ausgeführt wird und das Minimum unter allen ausgewählt wird. Die Zeitkomplexität dieses Prozesses ist O(nkr+2).
Algorithmus 1 Traversal-Phase nach Bestellung: Berechnen Sie die Kosten für jeden Zustand an jedem Scheitelpunkt
- 1:
Eingabe: Netzwerk N und die beobachteten Zustände von Σ an den Blättern von N, d. H. Eine Zustandszuordnungsfunktion λ über das Alphabet Σ für N.
- 2:
Für jedes Blatt v sei S v (i) = 0, wenn λ(v) = i und ∞ andernfalls.
- 3:
Wiederholen Sie in der Nachreihenfolge für jeden im internen Scheitelpunkt (Wurzel, interner Baumscheitelpunkt oder netzförmiger Scheitelpunkt) v in N: Berechnen Sie für jeden Zustand i SV (i) gemäß (1) und t (v, w) (i) für jedes Kind w von v gemäß (2).
- 4:
Ausgabe: {(S v (i), ): v ∈ V (N), i ∈ Σ}.
Minimierung der Anzahl der Mutationen in einem phylogenetischen Netzwerk
Der Fitch-Algorithmus zählt die Anzahl der Änderungen in einem sich verzweigenden phylogenetischen Baum für jeden Zeichensatz, wobei sich die Zustände von jedem Zustand in einen anderen Zustand ändern können. Somit ist die Kostenmatrix so, dass ihre diagonalen Elemente alle Nullen und die nicht diagonalen Elemente alle Einsen sind. In diesem Abschnitt zeigen wir, wie sich der Fitch-Algorithmus darauf erstreckt, obere und untere Grenzen für die Anzahl der evolutionären Veränderungen in einem bestimmten phylogenetischen Netzwerk zu finden. Zunächst zeigen wir, dass der Fitch-Algorithmus erweitert werden kann, um eine Obergrenze für den optimalen Sparsamkeitswert anzugeben. Wie zuvor sind die Nachbestellungs- und die Vorbestellungs-Traversal-Phasen in den Algorithmen 3 und 4 unten angegeben. Siehe Abbildung 3 für einen Beispiellauf des Algorithmus.

Fitch-Lösung. Die Fitch-Lösung wurde auf dasselbe phylogenetische Netzwerk und die Blattdaten in Abbildung 2 angewendet. Jedem Scheitelpunkt wird ein Satz aller möglichen Zustände zusammen mit einer Punktzahl zugewiesen, wenn die Netzwerkscheitelpunkte in Nachreihenfolge durchlaufen werden. Die Punktzahl an der Wurzel gibt eine Obergrenze für die optimale Punktzahl an. Die Zustandszuweisungen werden während der Pre-Order-Traversal-Phase gegeben und die Anzahl der Substitutionen stimmt mit der Punktzahl an der Wurzel überein.
Algorithmus 2 Vorbestellungsphase: Berechnen Sie untere und obere Grenzen des Optimums und die entsprechende Zuordnung der oberen Grenze
- 1:
Eingabe: {(S v (i), ): v ∈ V (N), i ∈ Σ}.
- 2:
Sei S = min i S r (i), wobei r der Wurzelscheitelpunkt ist und sei λ ^ ( r ) =arg min i S r ( i) .
- 3:
Sei S‘ = S
- 4:
Für jeden Scheitelpunkt w in der Vorreihenfolge, dessen übergeordneter Scheitelpunkt v unmittelbar vor w in der Vorreihenfolge steht, sei λ ^ (ω) = t v , w (i) , wobei i= λ ^ (v) .
- 5:
Besuchen Sie jeden retikulären Scheitelpunkt w mit den Eltern v und v‘, so dass w die Traversal-Bedingung in Bezug auf v erfüllt, mit i= λ ^ (v) , i ‚ = λ ^ (v ‚), j ‚ = t (v ‚, w ) ( i) und aktualisieren Sie S‘ wie folgt:
S ‚ ← S ‚ – c i ‚ j ‚ + c i ‚ j. - 6:
Ausgabe: (Untere Grenze, Obere Grenze) = (S, S‘); Erweiterung entsprechend der oberen Grenze Punktzahl S ‚ : λ ^ .
Algorithmus 3 Traversal-Phase nach Bestellung: Berechnen Sie das Optimum
- 1:
Eingabe: Phylogenetisches Netzwerk N und eine Zustandszuordnungsfunktion λ über das Alphabet Σ für N.
- 2:
Für jedes Blatt v von N erhalten wir A(v) = {λ(v)}, eine Singleton-Menge, die den beobachteten Zustand am Blatt enthält.
- 3:
Setze UB = 0.
- 4:
Rekursiv mit Nachbestellung: Für einen Scheitelpunkt v von T mit Kindern w1 und w2 sei und Wenn der Scheitelpunkt v ein einzelnes Kind w hat, dann
und
5: ({A(v): v ∈ V (N)}, UB)
Da die Pre-Order-Traversal-Phase eine konfliktfreie Zuweisung auf den Eckpunkten gibt, ist UB eine obere Grenze. Dies ist ein Sonderfall des dynamischen Algorithmus, der für die allgemeine Kostenmatrix dargestellt wird. Angenommen, wir beschränken N auf ein phylogenetisches Netzwerk ohne Schwesterretikulationen, dann bildet jede Fitch-Lösung für einen Baum T in T (N) eine Untergrenze für die optimale Punktzahl in Netzwerken; und das Hinzufügen der Kosten an Kanten, die nicht in T enthalten sind, ergibt eine Obergrenze für die optimale Punktzahl. Somit ist es möglich, unsere untere Grenze zum Zählen der Anzahl der Zeichenänderungen nur für phylogenetische Netzwerke ohne Schwesterretikulationen zu berechnen, bei denen es einfach ist, einen Baum in T (N) zu finden .
Algorithmus 4 Pre-order traversal phase: Zuweisen der Zustände
- 1:
Eingabe: Phylogenetischer Baum N und ({A(v): v ∈ V (N)}, UB).
- 2:
Für jeden Scheitelpunkt v im Baum, der noch nicht zugewiesen ist, berechnet der Algorithmus λ ^ ( v ) wie folgt: Für die Wurzel r gilt λ ^ ( r) =σ, wobei σ ein beliebiges Element von A(r) ist. Rekursiv über Vorbestellung zuweisen: Für einen Scheitelpunkt v, dessen übergeordnetes u zugewiesen ist,
λ ^ ( v ) = λ ^ ( u) wenn λ ^ ( u ) ∈ A (v); σ ∈ A ( v ) andernfalls . - 3:
Festlegen der Punktzahl: Wenn u‘ für jeden retikulären Scheitelpunkt v nicht das übergeordnete Element in der Vorreiterfolge ist und wenn λ ^ ( u ‚ ) ∈A ( v ) , aber λ ^ ( u ‚ ) ≠ λ ^ ( v) , erhöhen Sie UB um 1.
- 4:
Ausgabe: UB und Erweiterungsfunktion λ ^ von λ.