Normalverteilungen (Glockenkurve): Definition, Textaufgaben

Wahrscheinlichkeit und Statistik > Normalverteilungen

Inhalt:

1. Was ist eine Normalverteilung?
2. Das Standardnormalmodell
3. Normalverteilungsprobleme.
4. Normalverteilung auf dem TI 89 Beispiele
5. In Verbindung stehende Artikel.

Was ist eine Normalverteilung?

Eine Normalverteilung.

Eine Normalverteilung, manchmal auch Glockenkurve genannt, ist eine Verteilung, die in vielen Situationen natürlich vorkommt. Zum Beispiel wird die Glockenkurve in Tests wie dem SAT und GRE gesehen. Ein noch kleinerer Prozentsatz der Schüler erhält ein F oder ein A. Dies erzeugt eine Verteilung, die einer Glocke ähnelt (daher der Spitzname). Die Glockenkurve ist symmetrisch. Die Hälfte der Daten fällt links vom Mittelwert; Die Hälfte fällt nach rechts.
Viele Gruppen folgen diesem Muster. Deshalb ist es in der Wirtschaft, Statistik und in Regierungsbehörden wie der FDA weit verbreitet:

• Höhen von Menschen.
• Messfehler.
• Blutdruck.
• Punkte auf einem Test.
• IQ-Werte.
• Gehälter.

Die empirische Regel gibt an, wie viel Prozent Ihrer Daten innerhalb einer bestimmten Anzahl von Standardabweichungen vom Mittelwert liegen:
• 68% der Daten liegen innerhalb einer Standardabweichung vom Mittelwert.
* 95% der Daten liegen innerhalb von zwei Standardabweichungen des Mittelwerts.
* 99,7% der Daten liegen innerhalb von drei Standardabweichungen des Mittelwerts.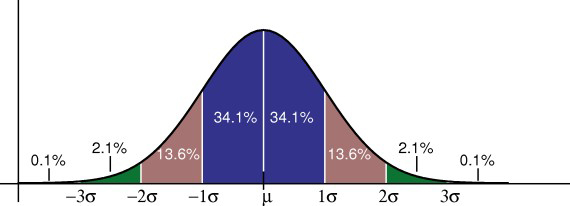

Die Standardabweichung steuert die Streuung der Verteilung. Eine kleinere Standardabweichung zeigt an, dass die Daten eng um den Mittelwert gruppiert sind. Eine größere Standardabweichung zeigt an, dass die Daten um den Mittelwert verteilt sind; Die Normalverteilung ist flacher und breiter.

Eigenschaften einer Normalverteilung

• Mittelwert, Modus und Median sind alle gleich.
• Die Kurve ist in der Mitte symmetrisch (d. H. um den Mittelwert μ).
• Genau die Hälfte der Werte befindet sich links von der Mitte und genau die Hälfte der Werte befindet sich rechts.
• Die Gesamtfläche unter der Kurve beträgt 1.

Das Standardnormalmodell
Ein Standardnormalmodell ist eine Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1.

Normales Standardmodell: Verteilung von Daten

Eine Möglichkeit, herauszufinden, wie Daten verteilt werden, besteht darin, sie in einem Diagramm darzustellen. Wenn die Daten gleichmäßig verteilt sind, können Sie eine Glockenkurve erstellen. Eine Glockenkurve hat einen kleinen Prozentsatz der Punkte an beiden Schwänzen und den größeren Prozentsatz am inneren Teil der Kurve. Im normalen Standardmodell würden etwa 5 Prozent Ihrer Daten in die „Schwänze“ fallen (im Bild unten dunkler orange gefärbt) und 90 Prozent liegen dazwischen. Zum Beispiel würde die Normalverteilung für Testergebnisse von Studenten zeigen, dass 2,5 Prozent der Studenten sehr niedrige Punktzahlen erhalten und 2.5 Prozent bekommen sehr hohe Punktzahlen. Der Rest wird in der Mitte sein; nicht zu hoch oder zu niedrig. Die Form der Standardnormalverteilung sieht folgendermaßen aus:

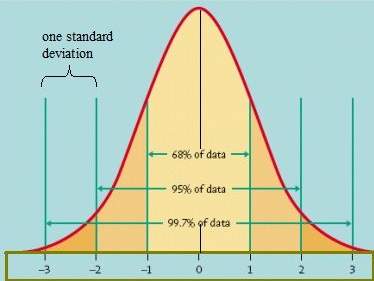
Standardnormalmodell. Bildnachweis: Universität von Virginia.

Praktische Anwendungen des Standardnormalmodells

Die Standardnormalverteilung könnte Ihnen helfen, herauszufinden, in welchem Fach Sie gute Noten erhalten und in welchen Fächern Sie sich aufgrund niedriger Scoring-Prozentsätze mehr anstrengen müssen. Sobald Sie eine Punktzahl in einem Fach erhalten, die höher ist als Ihre Punktzahl in einem anderen Fach, denken Sie vielleicht, dass Sie in dem Fach, in dem Sie die höhere Punktzahl erzielt haben, besser sind. Das stimmt nicht immer.

Sie können nur sagen, dass Sie in einem bestimmten Fach besser sind, wenn Sie eine Punktzahl mit einer bestimmten Anzahl von Standardabweichungen über dem Mittelwert erhalten. Die Standardabweichung gibt an, wie eng Ihre Daten um den Mittelwert gruppiert sind. Es ermöglicht Ihnen, verschiedene Verteilungen mit unterschiedlichen Datentypen zu vergleichen — einschließlich verschiedener Mittelwerte.

Zum Beispiel, wenn Sie eine Punktzahl von 90 in Mathe und 95 in Englisch bekommen, könnten Sie denken, dass Sie in Englisch besser sind als in Mathe. In der Mathematik liegt Ihre Punktzahl jedoch 2 Standardabweichungen über dem Mittelwert. Im Englischen ist es nur eine Standardabweichung über dem Mittelwert. Es sagt Ihnen, dass Ihre Punktzahl in Mathematik weitaus höher ist als bei den meisten Schülern (Ihre Punktzahl fällt in den Schwanz).
Basierend auf diesen Daten haben Sie in Mathe tatsächlich besser abgeschnitten als in Englisch!

Wahrscheinlichkeitsfragen unter Verwendung des Standardmodells

Fragen zur Standardnormalverteilungswahrscheinlichkeit können alarmierend aussehen, aber der Schlüssel zu ihrer Lösung besteht darin, zu verstehen, was die Fläche unter einer Standardnormalkurve darstellt. Die Gesamtfläche unter einer Standardnormalverteilungskurve beträgt 100% (das ist „1“ als Dezimalzahl). Zum Beispiel ist die linke Hälfte der Kurve 50%, oder .5. Die Wahrscheinlichkeit, dass eine Zufallsvariable in der linken Hälfte der Kurve erscheint, ist also .5.

Natürlich sind nicht alle Probleme so einfach, weshalb es eine Z-Tabelle gibt. Eine z-Tabelle misst nur diese Wahrscheinlichkeiten (dh 50%) und setzt sie in Standardabweichungen vom Mittelwert. Der Mittelwert liegt in der Mitte der Standardnormalverteilung, und eine Wahrscheinlichkeit von 50% entspricht null Standardabweichungen.

Standardnormalverteilung: So finden Sie die Wahrscheinlichkeit (Schritte)

Schritt 1: Zeichnen Sie eine Glockenkurve und schattieren Sie den Bereich, nach dem in der Frage gefragt wird. Das folgende Beispiel zeigt z >-0.8. Das heißt, Sie suchen nach der Wahrscheinlichkeit, dass z größer als -0,8 ist, also müssen Sie eine vertikale Linie bei -0 zeichnen.8 Standardabweichungen vom Mittelwert und schattieren alles, was größer als diese Zahl ist.

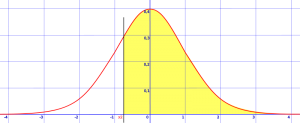
Schattierter Bereich ist z > -0.8

Schritt 2: Besuchen Sie den Normal probability Area Index und suchen Sie ein Bild, das wie Ihr Diagramm aussieht. Befolgen Sie die Anweisungen auf dieser Seite, um den Z-Wert für das Diagramm zu ermitteln. Der z-Wert ist die Wahrscheinlichkeit.Tipp: Schritt 1 ist technisch optional, aber es ist immer eine gute Idee, ein Diagramm zu skizzieren, wenn Sie versuchen, Wahrscheinlichkeitsaufgaben zu beantworten. Das liegt daran, dass die meisten Fehler nicht passieren, weil Sie nicht rechnen oder eine Z-Tabelle lesen können, sondern weil Sie einen Z-Score subtrahieren, anstatt zu addieren (dh Sie stellen sich die Wahrscheinlichkeit unter der Kurve in die falsche Richtung vor. Eine Skizze hilft Ihnen, genau das, wonach Sie suchen, in Ihrem Kopf zu zementieren.

Wenn Sie immer noch Probleme haben, schauen Sie sich die Tutoren an Chegg.com . Ihre ersten 30 Minuten mit einem Live-Tutor sind kostenlos!

Normalverteilung Wortprobleme

Dieses Video zeigt ein Beispiel für eine Normalverteilung Wortproblem. Für weitere Beispiele, lesen Sie weiter unten:

Wenn Sie die Normalverteilung in einer Statistikklasse angehen, versuchen Sie, die Fläche unter der Kurve zu finden. Die Gesamtfläche beträgt 100% (als Dezimalzahl 1). Normalverteilungsprobleme gibt es in sechs Grundtypen. Woher wissen Sie, dass ein Wortproblem eine Normalverteilung beinhaltet? Suchen Sie nach dem Schlüsselwort „Angenommen, die Variable ist normalverteilt“ oder „Angenommen, die Variable ist ungefähr normal.“ Um ein Wortproblem zu lösen, müssen Sie herausfinden, welchen Typ Sie haben.

1. „Zwischen“: Enthalten die Phrase „zwischen“ und enthält eine obere Grenze und untere Grenze (dh „Finden Sie die Anzahl der Häuser preislich zwischen $50K und 200K“).
2. „More Than“ oder „Above“: enthält den Ausdruck „more than“ oder „above“.
3. „Kleiner als“.
4. Lower Cut Off Example (video)
5. Upper Cut Off Example (Video)
6. Middle Percent Example (Video)

„Between“

Diese Anleitung behandelt die Lösung von Problemen, die den Ausdruck „between“ enthalten und eine obere und untere Grenze enthalten (dh „Finden Sie die Anzahl der Häuser zwischen $ 50K und 200K“. Beachten Sie, dass dies anders ist als das Finden des „mittleren Prozentsatzes“ von etwas.

Wortprobleme mit Normalverteilung: „Zwischen“: Schritte

Schritt 1: Identifizieren Sie die Teile des Wortproblems. Das Wort Problem wird identifizieren:

1. Der Mittelwert (Durchschnitt oder μ).
2. Standardabweichung (σ).
3. Nummer ausgewählt (d. h. „Wähle eine nach dem Zufallsprinzip“ oder „Wähle zehn nach dem Zufallsprinzip“).
4. X: Die mit „between“ verknüpften Zahlen (dh „between $5,000 and $10,000“ hätten X als 5,000 und als $ 10,000).

Zusätzlich erhalten Sie ENTWEDER:

1. Stichprobengröße (d. H. 400 Häuser, 33 Personen, 99 Fabriken, 378 Klempner usw.). ODER
2. Sie werden möglicherweise nach einer Wahrscheinlichkeit gefragt (in diesem Fall ist Ihre Stichprobengröße höchstwahrscheinlich jeder, dh „Klempnergeselle“ oder „Erstes Jahr“.“

Schritt 2: Zeichnen Sie ein Diagramm. Setzen Sie den Mittelwert, den Sie in Schritt 1 identifiziert haben, in die Mitte. Setzen Sie die mit „zwischen“ verknüpfte Zahl in die Grafik (raten Sie, wo die Zahlen fallen würden – es muss nicht genau sein). Wenn Ihr Mittelwert beispielsweise 100 US-Dollar betrug und Sie nach „Stundenlöhnen zwischen 75 und 125 US-Dollar“ gefragt wurden, sieht Ihr Diagramm ungefähr so aus:

Schritt 3:Ermitteln Sie die Z-Werte. Stecken Sie den ersten X-Wert (in meinem Diagramm oben ist es 75) in die Z-Wertformel und lösen Sie. Der μ (der Mittelwert) ist 100 aus dem Stichprobendiagramm. Sie können diese Zahlen (einschließlich σ, der Standardabweichung) aus Ihren Antworten in Schritt 1 abrufen :

*Hinweis: Wenn Sie die Formel verwirrt, werden Sie von dieser Formel nur aufgefordert:
1. Subtrahieren Sie den Mittelwert von X
2. dividieren Sie durch die Standardabweichung.

Schritt 4: Wiederholen Sie Schritt 3 für das zweite X.

Schritt 5: Nehmen Sie die Zahlen aus Schritt 3 und 4 und verwenden Sie sie, um den Bereich in der Z-Tabelle zu finden.

Wenn Sie gebeten wurden, eine Wahrscheinlichkeit in Ihrer Frage zu finden, gehen Sie zu Schritt 6a. Wenn Sie gebeten wurden, eine Zahl aus einer bestimmten Stichprobengröße zu finden, gehen Sie zu Schritt 6b.

Schritt 6a:

Wandle die Antwort aus Schritt 5 in einen Prozentsatz um.

Zum Beispiel ist 0,1293 12,93%.

Das war’s – überspringen Sie Schritt 6b!

Schritt 6b

Multiplizieren Sie die Stichprobengröße (gefunden in Schritt 1) mit dem z-Wert, den Sie in Schritt 4 gefunden haben. Zum Beispiel 0,300 * 100 = 30.

Das war’s!

„Mehr als“ oder „Über“

Diese Anleitung behandelt die Lösung von Normalverteilungsproblemen, die den Ausdruck „mehr als“ (oder einen Ausdruck wie „über“) enthalten.

Schritt 1: Zerlegen Sie das Wortproblem in Teile. Finden:

1. Der Mittelwert (Durchschnitt oder μ)
2. Standardabweichung (σ)
3. Eine Zahl (z. B. „Wähle fünfzig nach dem Zufallsprinzip“ oder „wähle 90 nach dem Zufallsprinzip“)
4. X: Die Zahl, die der Anweisung „kleiner als“ zugeordnet ist. Wenn Sie beispielsweise aufgefordert wurden, „unter 9.999 US-Dollar“ zu finden, ist X 9.999.

Schritt 2: Finden Sie die Probe aus dem Problem. Sie haben entweder eine bestimmte Größe (wie „1000 Fernseher“) oder eine allgemeine Stichprobe („Jeder Fernseher“).

Zeichnen Sie ein Bild, wenn das Problem mit dem Mittelwert und dem Bereich, den Sie suchen. Wenn der Mittelwert beispielsweise 15 US-Dollar beträgt und Sie gefragt wurden, was mehr als 10 US-Dollar kosten würde, könnte Ihr Diagramm folgendermaßen aussehen:

Schritt 3: Berechnen Sie den Z-Score (geben Sie Ihre Werte in die Z-Wertformel ein und lösen Sie sie). Verwenden Sie Ihre Antworten aus Schritt 1 :

Grundsätzlich subtrahieren Sie mit der Formel nur den Mittelwert von X und dividieren diese Antwort dann durch die Standardabweichung.

Schritt 4: Finden Sie den Bereich mit dem Z-Score aus Schritt 3. Verwenden Sie die Z-Tabelle. Nicht sicher, wie man eine Z-Tabelle liest? Sehen Sie das Video auf der z-Table-Seite.

Schritt 6: Gehen Sie zu Schritt 6a, um eine Wahrscheinlichkeit zu finden, ODER gehen Sie zu Schritt 6b, um eine bestimmte Zahl oder einen bestimmten Betrag zu berechnen.

Schritt 6a
Verwandeln Sie die Antwort von Schritt 5 in einen Prozentsatz.

Zum Beispiel ist 0,1293 12,93%.

Überspringen Sie Schritt 6b: Sie sind fertig!

Schritt 6b
Multiplizieren Sie die Stichprobengröße aus Schritt 1 mit dem Z-Score aus Schritt 4. Zum Beispiel 0,500 * 100 = 50.

Fertig!

Kleiner als

Diese Anleitung behandelt das Lösen von Normalverteilungsproblemen, die den Ausdruck „kleiner als“ (oder einen ähnlichen Ausdruck wie „weniger als“) enthalten.

Normalverteilung Wortprobleme kleiner als: Schritte

Schritt 1: Zerlegen Sie das Wortproblem in Teile:

1. Der Mittelwert (Durchschnitt oder μ)
2. Standardabweichung (σ)
3. Anzahl ausgewählt (d.h. „choose one at random“ oder „select ten at random“)
4. X: Die Zahl, die mit „less than“ einhergeht (d. H. „under $ 99,000“ würde X als 99,000 auflisten)

Außerdem haben Sie ENTWEDER:

1. Eine bestimmte Stichprobengröße. Zum Beispiel 500 Boote, 250 Sandwiches, 100 Fernseher usw.
2. Jeder in der Stichprobe (Sie werden aufgefordert, eine Wahrscheinlichkeit zu finden). Zum Beispiel „Medizinstudenten im ersten Jahr“, „Krebspatienten“ oder „Piloten.“

Schritt 2: Zeichnen Sie ein Bild, um das Problem zu visualisieren. Die folgende Grafik zeigt einen Mittelwert von 15 und eine Fläche „unter 4“):

Schritt 3: Ermitteln Sie den z-Wert, indem Sie die angegebenen Werte in die Formel einfügen. Das „X“ in unserem Beispieldiagramm ist 4 und der μ (oder Mittelwert) ist 15. Sie können diese Zahlen (einschließlich σ, der Standardabweichung) aus Ihren Antworten in Schritt 1 erhalten, in dem Sie die Teile des Problems identifiziert haben:

Alles, was Sie tun müssen, um die Formel zu lösen, ist:

1. Subtrahiere den Mittelwert von X.
2. Dividiere durch die Standardabweichung.

Schritt 4: Nehmen Sie die Nummer aus Schritt 3 und verwenden Sie dann die Z-Tabelle, um den Bereich zu finden.

Schritt 5:Um eine Wahrscheinlichkeit zu finden, gehen Sie zu Schritt 6a. Um eine Zahl aus einer bestimmten Stichprobengröße zu finden, gehen Sie zu Schritt 6b.

Schritt 6a

Ändern Sie die Zahl von Schritt 5 in Prozent.

Zum Beispiel ist 0,1293 12,93%.

Das war’s!

Schritt 6b

Multiplizieren Sie die Stichprobengröße (gefunden in Schritt 1) mit dem z-Wert, den Sie in Schritt 4 gefunden haben. Zum Beispiel 0,300 * 100 = 30.

Das war’s!

Unterer Grenzwert

Manchmal werden Sie bei einem Normalverteilungswortproblem aufgefordert, eine „untere Grenze eines oberen Prozentsatzes“ von etwas zu finden (dh „Finden Sie den Grenzwert, um eine bestimmte Prüfung zu bestehen, an der die oberen 40% der Testteilnehmer bestehen“). Ein niedrigerer Cut-Off-Punkt ist der Punkt, an dem die Punktzahlen unter diesen Punkt fallen. Beispielsweise möchten Sie möglicherweise herausfinden, wo sich der Grenzwert für die unteren 10% der Testteilnehmer befindet.

Schauen Sie sich unseren YouTube-Kanal an, um mehr über Probleme zu erfahren.

Normalverteilung TI 89 Beispiele

In der elementaren Statistik werden Sie oft mit einer Frage konfrontiert, die Sie nach den Grenzwerten für einen bestimmten Prozentsatz der Normalverteilung fragt, wie die oberen 90% oder die oberen 10%. Während die arbeit aus dieser art von problemen von hand ist umständlich, die TI-89 grafik-taschenrechner macht licht arbeit von finden cut off punkte für eine top prozentsatz mit die Inverse Normale funktion. Was Sie tatsächlich tun, ist nach den Cut-Off-Punkten für ein bestimmtes Perzentil zu suchen: wenn Sie beispielsweise eine Liste von Noten haben und wissen möchten, welche Punktzahl im 99. Perzentil liegt, können Sie die Funktion inverse Normal verwenden, um diesen prozentualen Grenzwert zu ermitteln.

Cut-Off-Punkte für einen oberen Prozentsatz finden

Beispielproblem: Studenten an einem bestimmten College sind durchschnittlich 5 Fuß 8 Zoll (68 Zoll) groß. Die Höhen sind normal verteilt, mit einer Standardabweichung von 2,5 Zoll. Was ist der Wert, der die oberen 1% der Höhen vom Rest der Bevölkerung trennt?

Schritt 1: Drücken Sie APPS und verwenden Sie die Scroll-Tasten, um Stats/List Editor zu markieren.

Schritt 2: Drücken Sie F5 2 1 (dies bringt Sie zum inversen normalen Bildschirm).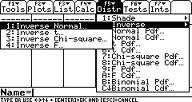

Schritt 3: Geben Sie 0,99 in das Feld Bereich ein.

Schritt 4: Geben Sie 68 in das Suchfeld ein.

Schritt 5: Geben Sie 2.5 in das Feld σ ein.

Schritt 6: Drücken Sie die EINGABETASTE.

Schritt 7: Lesen Sie die Ergebnisse: Inverse = 73,8159 bedeutet, dass die Schnitthöhe für das 99. Perzentil 73,8159 Zoll beträgt.

Das war’s!

Wahrscheinlichkeitsanteil Beispiel (NormalCDF-Funktion)

Beispielfrage: Eine Gruppe von Studenten mit normalverteilten Gehältern verdient durchschnittlich 6.800 US-Dollar mit einer Standardabweichung von 2.500 US-Dollar. Welcher Anteil der Studenten verdient zwischen 6.500 und 7.300 US-Dollar?

Schritt 1: Drücken Sie APPS. Scrollen Sie zum Statistik- / Listeneditor und drücken Sie die EINGABETASTE.

Schritt 2: Drücken Sie F5 4.

Schritt 3: Geben Sie 6500 in das Feld unterer Wert ein.

Schritt 4: Geben Sie 7300 in das obere Wertefeld ein.

Schritt 5: Geben Sie 6800 in das Suchfeld ein.

Schritt 6: Geben Sie 2500 in das Eingabefeld ein. EINGABETASTE.

Schritt 7: Lesen Sie die Antwort. In: Cdf=.127018. Mit anderen Worten, .013, oder 13% der Studenten verdienen zwischen $ 6,500 und $ 7,300.

TI-89 Normalverteilungskurve grafisch darstellen

Der TI-89 kann nicht nur Z-Scores und Rückgabewerte für Normalverteilungen berechnen, sondern auch die Normalverteilungskurve grafisch darstellen. Das Zeichnen einer Normalverteilung kann Ihnen helfen zu sehen, wonach Sie suchen sollen, und gibt Ihnen ein weiteres Werkzeug zur Lösung von Normalverteilungsproblemen. Der TI-89 kann eine Normalverteilungskurve mit einer für jeden Wert schattierten Fläche grafisch darstellen. Sie können beispielsweise ein Diagramm erstellen, das: kleiner als eine bestimmte Zahl, größer als eine bestimmte Zahl oder dazwischen eine bestimmte Menge von Zahlen.

Beispielproblem: Zeichnen Sie eine Normalverteilungskurve für studentische Gehälter während eines typischen Semesters. Die Gehälter der Studenten haben einen Mittelwert von $ 6.800 und eine Standardabweichung von $ 2.500. Schattieren Sie den Bereich in der Grafik, der Gehältern zwischen 7.300 und 9.000 US-Dollar entspricht.

Schritt 1: Drücken Sie APPS und wählen Sie den Statistik- / Listeneditor.

Schritt 2: Drücken Sie F2 3 und F2 4.

Schritt 3: Drücken Sie F5 ) 1.

Schritt 4: Scrollen Sie nach unten und geben Sie 7300 in das untere Wertefeld ein.

Schritt 5: Scrollen Sie nach unten und geben Sie 9000 in das obere Wertefeld ein.

Schritt 6: Scrollen Sie nach unten und geben Sie 6800 in das Suchfeld ein.

Schritt 7: Scrollen Sie nach unten und geben Sie 2500 in das Suchfeld ein.

Schritt 8: Scrollen Sie nach unten. Stellen Sie die automatische Skalierung auf „Ja“, indem Sie die rechte Bildlauftaste und dann die Bildlauftaste nach unten drücken, um Ja auszuwählen. EINGABETASTE.

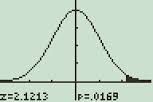
Ein Normalverteilungsdiagramm, das auf dem TI-89-Rechner angezeigt wird.

Das war’s!

Tipp: Wenn Sie ∞ (unendlich) als einen Ihrer unteren oder oberen Werte eingeben möchten, drücken Sie die Raute-Taste und dann Katalog.

Beyer, W. H. SFB Mathematische Standardtabellen, 28. Aufl. Boca Raton, FL: CRC Press, S. 533-534, 1987.Feller, W. Eine Einführung in die Wahrscheinlichkeitstheorie und ihre Anwendungen, Vol. 1, 3. Aufl. New York: Wiley, 1968.Kenney, J. F. und Keeping, E. S. Mathematik der Statistik, Pt. 2, 2. Aufl. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. „Die Fehlerkurve.“ §6.4 in mathematischen Nachbildungen. New York: W. W. Norton, S. 121-123, 1942.Patel, J. K. und Read, C. B. Handbuch der Normalverteilung. New York: Dekker, 1982.

1. Was ist die 68-95-99.7 Regel?
2. Box-Cox-Transformation
3. Box-Muller-Transformation
4. Gaußsche Mischungsmodelle.
5. Was ist ein normales Wahrscheinlichkeitsdiagramm?
6. So berechnen Sie einen Z-Score in der Statistik
7. Finden Sie den Bereich rechts von einem Z-Score.
8. Verwendung der normalen Approximation zur Lösung eines Binomialproblems
9. Was ist der Kontinuitätskorrekturfaktor?
10. Fläche unter einem Normalverteilungskurvenindex
11. Zentraler Grenzwertsatz.
12. Die Skew-Normalverteilung.
13. Zweischwänzige normale Kurve.
14. Die Q-Funktion.

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Deine ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!