Phasenumtastung

Konstellationsdiagramm für QPSK mit Graukodierung. Jedes benachbarte Symbol unterscheidet sich nur um ein Bit.

Manchmal wird dies als Quadriphase PSK, 4-PSK oder 4-QAM bezeichnet. (Obwohl die Wurzelkonzepte von QPSK und 4-QAM unterschiedlich sind, sind die resultierenden modulierten Radiowellen genau gleich.) QPSK verwendet vier Punkte auf dem Konstellationsdiagramm, die in gleichem Abstand um einen Kreis angeordnet sind. Mit vier Phasen kann QPSK zwei Bits pro Symbol codieren, wie im Diagramm mit Graucodierung gezeigt, um die Bitfehlerrate (BER) zu minimieren – manchmal falsch wahrgenommen als das Doppelte der BER von BPSK.Die mathematische Analyse zeigt, dass QPSK entweder verwendet werden kann, um die Datenrate im Vergleich zu einem BPSK-System zu verdoppeln, während die gleiche Bandbreite des Signals beibehalten wird, oder um die Datenrate von BPSK beizubehalten, aber die benötigte Bandbreite zu halbieren. In diesem letzteren Fall ist die BER von QPSK genau die gleiche wie die BER von BPSK – und anders zu glauben ist eine häufige Verwirrung bei der Betrachtung oder Beschreibung von QPSK. Der übertragene Träger kann eine Anzahl von Phasenänderungen erfahren.

Angesichts der Tatsache, dass Funkkommunikationskanäle von Agenturen wie der Federal Communications Commission mit einer vorgeschriebenen (maximalen) Bandbreite zugewiesen werden, wird der Vorteil von QPSK gegenüber BPSK deutlich: QPSK überträgt die doppelte Datenrate in einer gegebenen Bandbreite im Vergleich zu BPSK – bei gleicher BER. Die Engineering-Strafe, die bezahlt wird, ist, dass QPSK-Sender und -Empfänger komplizierter sind als die für BPSK. Bei moderner Elektroniktechnologie sind die Kosten jedoch sehr moderat.

Wie bei BPSK gibt es Phasenmehrdeutigkeitsprobleme auf der Empfangsseite, und differentiell codiertes QPSK wird in der Praxis häufig verwendet.

ImplementationEdit

Die Implementierung von QPSK ist allgemeiner als die von BPSK und zeigt auch die Implementierung von PSK höherer Ordnung an. Schreiben der Symbole in das Konstellationsdiagramm in Bezug auf die Sinus− und Cosinuswellen, die verwendet werden, um sie zu übertragen:

s n ( t ) = 2 E s T s cos ⁡ ( 2 π f c t + ( 2 n – 1 ) π 4 ) , n = 1 , 2 , 3 , 4. {\displaystyle s_{n}(t)={\sqrt {\frac {2E_{s}}{T_{s}}}}\cos \links(2\pi f_{c}t+(2n-1){\frac {\pi }{4}}\rechts),\quad n=1,2,3,4.}

Daraus ergeben sich je nach Bedarf die vier Phasen π/4, 3π/4, 5π/4 und 7π/4.

Daraus ergibt sich ein zweidimensionaler Signalraum mit Einheits-Basisfunktionen

ϕ 1 (t ) = 2 T s cos ⁡ (2 π f c t ) ϕ 2 (t ) = 2 T s sin ⁡ (2 π f c t ) {\displaystyle {\begin{1}\phi _{1}(t)&={\sqrt {\frac {2}{T_{s}}}}\cos \left (2\pi f_{c}t\rechts)\\\phi _{2}(t)&={\sqrt {\frac {2}{T_{s}}}}\sin \links(2\pi f_{c}t\rechts)\end{ausgerichtet}}}

Die erste Basisfunktion wird als gleichphasige Komponente des Signals und die zweite als Quadraturkomponente des Signals verwendet.

Somit besteht die Signalkonstellation aus dem Signalraum 4 Punkte

(± E s 2 ± E s 2). {\displaystyle {\begin{pmatrix}\pm {\sqrt {\frac {E_{s}}{2}}}&\pm {\sqrt {\frac {E_{s}}{2}}}\Ende{pmatrix}}.}

Die Faktoren 1/2 geben an, dass die Gesamtleistung gleichmäßig zwischen den beiden Trägern aufgeteilt wird.

Der Vergleich dieser Basisfunktionen mit der für BPSK zeigt deutlich, wie QPSK als zwei unabhängige BPSK-Signale betrachtet werden kann. Beachten Sie, dass die Signalraumpunkte für BPSK die Symbol- (Bit-) Energie nicht auf die beiden Träger in dem im BPSK-Konstellationsdiagramm gezeigten Schema aufteilen müssen.

QPSK-Systeme können auf verschiedene Arten implementiert werden. Eine Illustration der Hauptkomponenten der Sender- und Empfängerstruktur sind unten gezeigt.

Konzeptionelle Senderstruktur für QPSK. Der binäre Datenstrom wird in die In-Phase- und Quadraturphasenkomponenten aufgeteilt. Diese werden dann getrennt auf zwei orthogonale Basisfunktionen moduliert. In dieser Implementierung werden zwei Sinuskurven verwendet. Danach werden die beiden Signale überlagert, und das resultierende Signal ist das QPSK-Signal. Beachten Sie die Verwendung von polar Non-Return-to-Zero-Codierung. Diese Kodierer können vor für binäre Datenquelle gesetzt werden, aber sind danach gesetzt worden, um den konzeptionellen Unterschied zwischen den digitalen und analogen Signalen zu veranschaulichen, die mit digitaler Modulation miteinbezogen werden.

Empfängerstruktur für QPSK. Die angepassten Filter können durch Korrelatoren ersetzt werden. Jede Detektionsvorrichtung verwendet einen Referenzschwellwert, um zu bestimmen, ob eine 1 oder 0 detektiert wird.

Fehlerwahrscheinlichkeitbearbeiten

Obwohl QPSK als quartäre Modulation angesehen werden kann, ist es einfacher, es als zwei unabhängig modulierte Quadraturträger zu sehen. Bei dieser Interpretation werden die geraden (oder ungeraden) Bits verwendet, um die Inphasenkomponente des Trägers zu modulieren, während die ungeraden (oder geraden) Bits verwendet werden, um die Quadraturphasenkomponente des Trägers zu modulieren. BPSK wird auf beiden Trägern verwendet und kann unabhängig voneinander demoduliert werden.

Infolgedessen ist die Wahrscheinlichkeit eines Bitfehlers für QPSK dieselbe wie für BPSK:

P b = Q (2 E b N 0 ) {\displaystyle P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)}

m die gleiche Bitfehlerwahrscheinlichkeit wie BPSK zu erreichen, verwendet QPSK die doppelte Leistung (da zwei Bits gleichzeitig übertragen werden).

Die Symbolfehlerrate ist gegeben durch:

P s = 1 − ( 1 − P b ) 2 = 2 Q ( E s N 0 ) − 2 . {\displaystyle {\begin{b}P_{s}&=1-\links(1-P_{b}\rechts)^{2}\\&=2Q\links({\sqrt {\frac {E_{s}}{N_{0}}}}\rechts)-\links^{2}.\end{aligned}}}

Wenn das Signal-Rausch-Verhältnis hoch ist (wie es für praktische QPSK-Systeme erforderlich ist), kann die Wahrscheinlichkeit eines Symbolfehlers angenähert werden:

P s ≈ 2 Q ( E s N 0 ) = erfc ⁡ ( E s 2 N 0 ) = erfc ⁡ (E b N 0 ) {\displaystyle P_{s}\ungefähr 2Q\links({\sqrt {\frac {E_{s}}{N_{0}}}}\rechts)=\operatorname {erfc} \links({\sqrt {\frac {E_{s}}{2N_{0}}}}\rechts)=\Operatorname {erfc} \left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)}

Das modulierte Signal wird unten für ein kurzes Segment eines binärer Datenstrom. Die beiden Trägerwellen sind eine Kosinuswelle und eine Sinuswelle, wie aus der obigen Signalraumanalyse hervorgeht. Dabei sind die ungeraden Bits der Inphasenkomponente und die geraden Bits der Quadraturkomponente zugeordnet (wobei das erste Bit als Nummer 1 gilt). Das Gesamtsignal – die Summe der beiden Komponenten – wird unten angezeigt. Phasensprünge sind zu sehen, wenn der PSK die Phase jeder Komponente zu Beginn jeder Bitperiode ändert. Die oberste Wellenform allein entspricht der obigen Beschreibung für BPSK.

Zeitdiagramm für QPSK. Unterhalb der Zeitachse ist der binäre Datenstrom dargestellt. Oben sind die beiden Signalkomponenten mit ihren Bitbelegungen und unten das gesamte kombinierte Signal dargestellt. Beachten Sie die abrupten Phasenänderungen an einigen Bitperiodengrenzen.

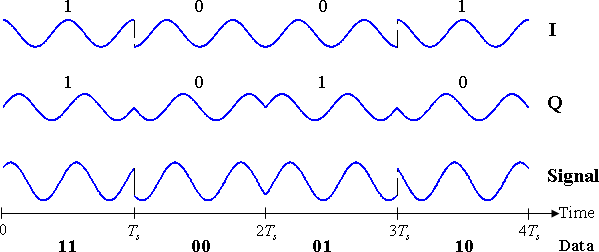
Die Binärdaten, die von dieser Wellenform übermittelt werden, lauten: 11000110.

• Die hier hervorgehobenen ungeraden Bits tragen zur In-Phase-Komponente bei: 11000110
• Die hier hervorgehobenen geraden Bits tragen zur Quadraturphasenkomponente bei: 11000110

VariantsEdit

Offset QPSK (OQPSK)Edit

Signal durchläuft den Ursprung nicht, da jeweils nur ein Bit des Symbols geändert wird.

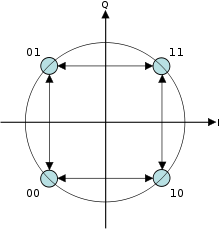
Offset Quadrature Phase-Shift Keying (OQPSK) ist eine Variante der Phase-Shift-Keying-Modulation mit vier verschiedenen Werten der Phase zu übertragen. Es wird manchmal staggered Quadrature Phase-Shift Keying (SQPSK) genannt.

Differenz der Phase zwischen QPSK und OQPSK

Wenn Sie vier Werte der Phase (zwei Bits) gleichzeitig verwenden, um ein QPSK-Symbol zu konstruieren, kann die Phase des Signals um bis zu 180 ° gleichzeitig springen. Wenn das Signal tiefpassgefiltert wird (wie es in einem Sender typisch ist), führen diese Phasenverschiebungen zu großen Amplitudenschwankungen, eine unerwünschte Qualität in Kommunikationssystemen. Durch Versetzen des Timings der ungeraden und geraden Bits um eine Bitperiode oder eine halbe Symbolperiode ändern sich die Inphase- und Quadraturkomponenten niemals gleichzeitig. In dem rechts gezeigten Konstellationsdiagramm ist zu erkennen, dass dadurch die Phasenverschiebung auf jeweils nicht mehr als 90 ° begrenzt wird. Dies ergibt viel geringere Amplitudenschwankungen als Nicht-Offset-QPSK und wird manchmal in der Praxis bevorzugt.

Das Bild rechts zeigt den Unterschied im Verhalten der Phase zwischen gewöhnlichem QPSK und OQPSK. Es ist zu sehen, dass sich die Phase im ersten Diagramm sofort um 180 ° ändern kann, während in OQPSK die Änderungen niemals größer als 90 ° sind.

Das modulierte Signal ist unten für ein kurzes Segment eines zufälligen binären Datenstroms dargestellt. Beachten Sie den halben Symbolperiodenversatz zwischen den beiden Komponentenwellen. Die plötzlichen Phasenverschiebungen treten etwa doppelt so häufig auf wie bei QPSK (da sich die Signale nicht mehr gemeinsam ändern), sind jedoch weniger stark ausgeprägt. Mit anderen Worten, die Größe der Sprünge ist in OQPSK im Vergleich zu QPSK geringer.

SOQPSKEdit

Das lizenzfreie Shaped-Offset QPSK (SOQPSK) ist mit Feher-patentiertem QPSK (FQPSK) interoperabel, in dem Sinne, dass ein Integrate-and-Dump Offset QPSK Detektor die gleiche Ausgabe erzeugt, egal welche Art von Sender verwendet wird.

Diese Modulationen formen die I- und Q-Wellenformen sorgfältig so, dass sie sich sehr sanft ändern und das Signal auch bei Signalübergängen mit konstanter Amplitude bleibt. (Anstatt sich sofort von einem Symbol zum anderen oder sogar linear zu bewegen, bewegt es sich sanft um den Kreis mit konstanter Amplitude von einem Symbol zum nächsten. Die SOQPSK-Modulation kann als Hybrid aus QPSK und MSK dargestellt werden: SOQPSK hat die gleiche Signalkonstellation wie QPSK, jedoch ist die Phase von SOQPSK immer stationär.

Die Standardbeschreibung von SOQPSK-TG beinhaltet ternäre Symbole. SOQPSK ist eines der am weitesten verbreiteten Modulationsschemata für die LEO-Satellitenkommunikation.

π/4-QPSKEdit

Doppelkonstellationsdiagramm für π/4-QPSK. Dies zeigt die beiden getrennten Konstellationen mit identischer Graukodierung, jedoch um 45 ° zueinander gedreht.

Diese Variante von QPSK verwendet zwei identische Konstellationen, die um 45° ( π / 4 {\displaystyle \pi /4}

Bogenmaß, daher der Name) zueinander gedreht sind. Normalerweise werden entweder die geraden oder ungeraden Symbole verwendet, um Punkte aus einer der Konstellationen auszuwählen, und die anderen Symbole wählen Punkte aus der anderen Konstellation aus. Dies reduziert auch die Phasenverschiebungen von maximal 180°, aber nur auf maximal 135° und so liegen die Amplitudenschwankungen von π/4 {\displaystyle \pi/4}

-QPSK zwischen OQPSK und nicht-offset QPSK. Eine Eigenschaft dieses Modulationsschemas ist, dass, wenn das modulierte Signal in der komplexen Domäne dargestellt wird, Übergänge zwischen Symbolen niemals 0 durchlaufen. Mit anderen Worten, das Signal passiert den Ursprung nicht. Dies verringert den dynamischen Bereich von Schwankungen im Signal, der bei der Entwicklung von Kommunikationssignalen wünschenswert ist.

Andererseits eignet sich π / 4 {\displaystyle \pi /4}

-QPSK für eine einfache Demodulation und wurde beispielsweise für die Verwendung in TDMA-Mobiltelefonsystemen übernommen.

Das modulierte Signal ist unten für ein kurzes Segment eines zufälligen binären Datenstroms dargestellt. Die Konstruktion ist die gleiche wie oben für gewöhnliche QPSK. Aufeinanderfolgende Symbole werden aus den beiden im Diagramm gezeigten Konstellationen entnommen. Somit wird das erste Symbol (1 1) aus der Konstellation „blau“ und das zweite Symbol (0 0) aus der Konstellation „grün“ entnommen. Beachten Sie, dass sich die Größen der beiden Komponentenwellen ändern, wenn sie zwischen Konstellationen wechseln, aber die Größe des Gesamtsignals bleibt konstant (konstante Hüllkurve). Die Phasenverschiebungen liegen zwischen denen der beiden vorherigen Zeitdiagramme.

Zeitdiagramm für π/4-QPSK. Unterhalb der Zeitachse ist der binäre Datenstrom dargestellt. Oben sind die beiden Signalkomponenten mit ihren Bitbelegungen und unten das gesamte, kombinierte Signal dargestellt. Beachten Sie, dass aufeinanderfolgende Symbole abwechselnd von den beiden Konstellationen genommen werden, beginnend mit dem „blauen“.

DPQPSKEdit

Dual-Polarisation Quadrature Phase Shift Keying (DPQPSK) oder Dual-Polarisation QPSK – beinhaltet das Polarisationsmultiplexen von zwei verschiedenen QPSK-Signalen, wodurch die spektrale Effizienz um den Faktor 2 verbessert wird. Dies ist eine kostengünstige Alternative zur Verwendung von 16-PSK anstelle von QPSK, um die spektrale Effizienz zu verdoppeln.