Häresie gibt es auf verschiedenen Ebenen. Für den modernen Intellektuellen könnte die niedrigste Stufe der Häresie in Politik oder Wirtschaft liegen – Denkbereiche, in denen man unorthodoxe Ideen haben darf, ohne von höflicher Gesellschaft ausgeschlossen zu werden. Höhere Ebenen der Häresie könnten sich auf Religion oder Wissenschaft beziehen – stimmen Sie hier nicht mit orthodoxen Annahmen überein, und Sie werden als ziemlich verrückt angesehen. Die höchste Stufe der Häresie in der modernen Welt ist die mathematische Häresie. Uneinigkeit mit der mathematischen Orthodoxie ist gleichbedeutend mit „eine ausgewachsene Kurbel sein.“ Man darf einfach nicht an bestimmten Ideen in der Mathematik zweifeln, ohne als intellektueller Aussätziger verurteilt zu werden.Leider gibt es, wie in jedem anderen Bereich des Denkens, eine umgekehrte Beziehung zwischen „Akzeptanz von Meinungsverschiedenheiten“ und „Fehlerwahrscheinlichkeit“.“ Je tabuisierter es ist, eine Annahme in Frage zu stellen, desto wahrscheinlicher ist es, dass sie unter die Lupe genommen wird. Theologen mögen in der Lage sein, Meinungsverschiedenheiten über Gottes Eigenschaften zu tolerieren, aber sie können Meinungsverschiedenheiten über Gottes Existenz nicht tolerieren. Seine Existenz ist zu grundlegend, um sie zu revidieren. Wenn Gott nicht existiert, wird die gesamte theoretische Struktur, die auf dieser Annahme aufbaut, zerstört.
So ist es mit der Mathematik. Einige grundlegende Annahmen dürfen nicht in Frage gestellt werden und sind daher zu Dogmen geworden, was diesen Artikel zu einer mathematischen Häresie macht.
Ich habe die Grundlagen der Standardgeometrie untersucht und zwei Fehler gefunden – einen logischen, den anderen metaphysischen. Dieser Artikel konzentriert sich auf das Metaphysische. Wesentliche Objekte, die von Mathematikern beschrieben werden, existieren nicht. Daher sind alle Schlussfolgerungen, die auf der Grundlage der Existenz dieser Objekte abgeleitet werden, wahrscheinlich falsch.In diesem Fall ist die allgemein akzeptierte Behauptung, dass „Pi eine irrationale, transzendentale Zahl ist, deren Größe nicht durch endliche dezimale Expansion ausgedrückt werden kann“, aufgrund eines metaphysischen Fehlers falsch.
Pi ist eine rationale Zahl mit endlicher Dezimalerweiterung. Diese Idee, die zunächst unvorstellbar erscheinen mag, wird sich am Ende dieses Artikels als überwältigend vernünftig herausstellen.(Für den Rest dieses Artikels werde ich „Pi ist eine rationale Zahl mit endlicher Dezimalerweiterung“ als „Pi ist eine endliche Zahl“ oder einfacher „Pi ist endlich“ abkürzen.“)
Über Formen
Meine Behauptungen sind einfach und bewahren grundlegende geometrische Intuition. Zum Beispiel ist dies ein „Kreis“:

Dies ist eine „Linie“:

Und das sind „Punkte“:

Wenn Sie glauben, dass diese Objekte tatsächlich Kreise, Linien und Punkte sind, dann glauben auch Sie, dass pi endlich ist. Sie sehen, Mathematiker glauben nicht, dass diese Objekte als „Linien“ oder „Punkte“ gelten. In ihren Köpfen können Linien und Punkte nicht gesehen werden, und tatsächlich würden sie sagen, dass die obigen „Linien und Punkte“ nur unvollkommene Annäherungen von Linien und Punkten sind.
Um zu verstehen, warum, müssen wir eine Reihe von Fragen stellen, deren Antworten die Leute annehmen, wurden bereits aussortiert. Dies sind Fragen, die angeblich so offensichtlich sind, dass sie es nicht wert sind, gestellt zu werden. Und doch, wenn wir sie von Mathematikern fragen, bekommen wir zweifelhafte Antworten. Fragen wie:
Was ist eine „Form“?
Was ist eine „Linie“?
Was ist ein „Punkt“?
Was ist ein „Kreis“?
Was ist „Entfernung“?
Stellen Sie Ihrem Durchschnittsintellektuellen diese Fragen, und er wird Sie wahrscheinlich verspotten, weil er annimmt: „Jeder weiß, was eine Linie ist!“ Sie sind falsch. Ich für meinen Teil glaube nicht, dass Mathematiker wissen, was Linien sind. Und weil ihre Theorien auf ihren metaphysischen Behauptungen über „Linien und Punkte“ aufbauen, müssen die Theorien von Grund auf überarbeitet werden.
Ohne Länge, Breite oder Sinn
Da pi das Thema dieses Artikels ist, legen wir die Definition dar, die wir alle in der Schule gelernt haben:
Pi ist das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
Wir haben hier ein paar Schlüsselbegriffe: „das Verhältnis“, „ein Kreis“, „Umfang“ und „Durchmesser“.
Um zu verstehen, was pi ist, müssen wir verstehen, was diese anderen Begriffe bedeuten. Besonders dieser: „ein Kreis.“ Hier ist eine Definition:
Ein „Kreis“ ist eine Form, deren Grenze aus Punkten besteht, die gleich weit von einem festen Punkt entfernt sind.
Klingt vernünftig. Ein paar weitere Schlüsselbegriffe, die wir verstehen müssen: „Form“, „Grenze“ und „Punkte“.“ Wenn wir pi verstehen wollen, müssen wir verstehen, was Kreise sind, und wenn wir verstehen wollen, was Kreise sind, müssen wir zuerst verstehen, was „Punkte“ sind.
Hier finde ich den grundlegenden Fehler, der die orthodoxe Geometrie plagt: die Definition eines Punktes, aus dem alle anderen geometrischen Objekte konstruiert werden. Was ist ein Punkt? Es stellt sich heraus, dass es viele verschiedene Definitionen gibt. Wir beginnen mit Euklids ursprünglicher Definition, die mir gefällt.
Ein „Punkt“ ist das, was keinen Teil hat.
Wir werden später auf diese Definition zurückkommen. Hier ist noch einer:
Ein „Punkt“ ist eine genaue Position oder ein Ort in einer Ebene.
Nicht schlecht. Sie werden oft durch kleine Punkte dargestellt:

Diese intuitiven Definitionen sind jedoch in der modernen Mathematik nicht wirklich praktikabel. „Punkte“ sind in der orthodoxen Geometrie nicht wirklich per se „definiert“. Sie sollen in ihren Eigenschaften verstanden werden. Eine wesentliche Eigenschaft ist diese:
Punkte haben keine Länge, Fläche, Volumen oder andere dimensionale Attribute. Sie sind „nulldimensionale“ Objekte.
Dies ist absolut grundlegend für moderne Vorstellungen von Geometrie. Punkte können keine Länge, Breite oder Tiefe haben. Und doch sind alle Formen angeblich aus ihnen konstruiert. Sie könnten also fragen: „Moment mal, wie können Formen, die Dimensionen haben, aus einer Reihe von Punkten bestehen, die keine Dimensionen haben?“Das ist eine sehr gute Frage, und wenn Sie darauf bestehen, eine logische Antwort zu finden, werden Sie wie ich enden: sehr große Teile der orthodoxen Mathematik ablehnen.
Für einen Mathematiker besteht jede „Linie“ eigentlich aus einer unendlichen Anzahl von Punkten – dennoch ist jeder Punkt selbst ohne Dimension. Linien, die eine Länge haben, bestehen aus Punkten, die keine Länge haben. Wie macht das Sinn?
Das tut es nicht.
Es ist wie zu fragen: „Wie viele 0 musst du addieren, um eine 1 zu bekommen?“ Die Antwort liegt auf der Hand: Sie können nicht eine Reihe von 0 addieren und eine 1 erhalten – nicht einmal eine unendliche Menge von 0. Wenn ein Punkt null Dimensionen hat, spielt es keine Rolle, wie viele Sie zusammenstellen. Sie werden nie mit einem dimensionalen Objekt enden. Dies ist eine logische Notwendigkeit.
Wir haben also ein sehr großes Problem. Die wörtliche Grundlage, auf der die gesamte theoretische Struktur der modernen Geometrie aufgebaut ist – der „Punkt“ – ist zweifelhaft. Fehler auf dieser Ebene können katastrophal sein.
Formen ohne Form
Wenn sie konsistent sind, zwingt sich der Mathematiker schnell in ungerade Positionen. Zum Beispiel muss er zu dem Schluss kommen: „Wir können keine Formen sehen!“ Nehmen Sie das Beispiel dessen, was Nicht-Mathematiker eine „Linie“ nennen:

Sicherlich kann dies für einen Mathematiker keine Linie sein, da Linien angeblich nur eine eindimensionale Länge haben. Dieses Objekt hat sowohl Länge als auch Breite – es ist in zwei Dimensionen erweitert. Wie können wir diese Form nennen, wenn nicht eine „Linie“? Ich weiß es nicht – Sie müssen einen Mathematiker fragen.
Was ist mit einem zweidimensionalen Objekt: dem Kreis?

Natürlich kann dies kein Kreis sein. Dieses Objekt besteht aus Pixeln, nicht aus Punkten, und jedes Pixel selbst ist in zwei Dimensionen erweitert. Daher hat das Objekt raue Kanten und ist nicht perfekt glatt. Obwohl Laien es einen „Kreis“ nennen könnten,“Es ist nur eine bloße Annäherung an den mathematischen Kreis, manchmal auch „perfekter Kreis“ genannt.“
Dasselbe gilt für den mysteriösen „Punkt“:

Diese Objekte können auch nicht als „Punkte“ qualifiziert werden, da sie Dimensionen haben. Wir können sie schließlich sehen. Mathematische Objekte können nicht gesehen werden; sie können nicht visualisiert werden; sie können keine erweiterte – oder „tatsächliche“ – Form haben. Wenn ein Objekt tatsächlich eine Form hat, wenn es Platz einnimmt, dann muss es aus räumlich ausgedehnten Objekten bestehen, die Computerpixeln ähneln, nicht aus mathematischen Punkten.
Hinweis: Ich spreche nicht nur von „physischem Raum“ oder „physischer Form“. Ich spreche von Formen jeglicher Art. Was ich in meinem Gesichtsfeld sehe – Farbkleckse – haben Form, aber sie sind keine physischen Objekte. Sie selbst besetzen keinen physischen Raum. Sie sind mentale Repräsentationen, und sie bestehen aus ausgedehnten Lichtpunkten – Pixeln auf meinem mentalen Bildschirm.
Es stellt sich also eine natürliche Frage:
Hat jemals jemand diese mathematischen Formen in irgendeiner Weise gesehen oder erlebt? Hat jemand auch nur eine wahre „Linie“ oder „Kreis“ begegnet? Die Antwort muss ein nachdrückliches „Nein“ sein. Alle“Linien“ und „Kreise“, die wir tatsächlich erleben, haben Dimensionen. Sie sind aus einer endlichen Anzahl von Punkten aufgebaut, die selbst Dimensionen haben. Die Objekte, die wir erleben, bestehen aus Pixeln.
Die Bedeutung dieses Punktes kann nicht hoch genug eingeschätzt werden.Dies bedeutet, dass jeder „Kreis“, den Sie jemals gesehen haben – oder den ein Ingenieur jemals zu Papier gebracht hat – tatsächlich ein rationales Verhältnis seines Umfangs zu seinem Durchmesser hat. Jeder „Kreis“, der jemals angetroffen wurde, hat ein eindeutiges „pi“, das als Verhältnis zweier ganzer Zahlen ausgedrückt werden kann.
„Umfang“ kann für jeden Kreis, den wir erleben können, als „äußerste Grenze der Form“ verstanden werden, die selbst aus einer endlichen Anzahl von Pixeln besteht. Auch sein „Durchmesser“ ist eine einfache ganze Zahl – die Anzahl der Pixel, aus denen er besteht. Setzen Sie eine ganze Zahl als Zähler und eine ganze Zahl als Nenner, und Sie haben ein rationales pi.Tatsächlich sollten diese Wahrheiten selbst für Mathematiker unumstritten sein:
Jeder „Kreis“, dem Sie jemals begegnet sind, hat ausnahmslos einen rationalen, endlichen pi.
Kein „Kreis“, dem Sie jemals begegnet sind, hat ausnahmslos einen irrationalen pi.Das bedeutet also, dass meine Behauptungen über einen „rationalen pi“ für mindestens 99,9999% aller Formen, die wir „Kreise“ nennen, wahr sind. Es bedeutet auch, dass pi für jeden gegebenen Kreis einzigartig ist. Dies sollte jedoch nicht überraschen, wenn Sie über die Art der Verhältnisse nachdenken.
Stellen Sie sich vor, ich würde sagen: „Wie ist das Verhältnis von Höhe zu Länge eines Tisches?“
Sie würden natürlich antworten: „Welche Tabelle?“
Das gleiche gilt für Kreise. Es gibt kein „ein wahres Verhältnis namens „pi““ Aus dem gleichen Grund gibt es kein „ein wahres Verhältnis von Höhe zu Länge einer Tabelle.“ Jede Tabelle und jeder Kreis besteht aus einer endlichen Anzahl von Einheiten, die auf unterschiedliche Weise angeordnet sind, und daher variieren ihre Verhältnisse.
Nach der Standardgeometrie gibt es buchstäblich nur einen „Kreis“, für den meine Behauptungen nicht zutreffen: den sogenannten „Perfekten Kreis“ – ein Objekt, das so mysteriös ist, dass kein Sterblicher ihm jemals begegnet ist.
Die göttliche Form
Dieser „perfekte Kreis“ hat keine messbaren Seiten oder Kanten. Seine Grenze besteht aus einer unendlichen Anzahl von nulldimensionalen Punkten. Die äußersten Punkte nehmen genau null Platz ein. Sein pi kann nicht durch eine dezimale Erweiterung ausgedrückt werden – noch werden wir jemals genau wissen, was sein Pi ist.
Dieses Objekt kann nicht konstruiert, visualisiert oder gar in unserer Welt existieren. Unsere Welt ist zu unvollkommen dafür. Stattdessen lebt es in einem anderen Bereich, auf den unser Verstand nur schwach zugreifen kann.
Der perfekte Kreis ist so groß, dass alle anderen „Kreise“ nur Annäherungen daran sind. Es ist der einzig wahre Kreis. Wenn Sie nach Beweisen für seine Existenz fragen, werden Sie keinen finden. Dennoch haben die Mathematiker ihre gesamte geometrische Theorie auf der Grundlage ihrer Existenz aufgebaut.
Ich gebe meine Häresie frei zu: Ich glaube nicht an den „perfekten Kreis“.“
Daher glaube ich nicht an das „Irrationale“.“ Ich habe auch keinen Bedarf an einem solchen Konzept. Jede Form, der ich jemals begegnet bin oder begegnen werde, hat Kanten, die Platz beanspruchen.Eine Geometrie ohne perfekte Kreise und ohne den irrationalen pi reicht völlig aus, um alle Phänomene zu erklären, die ich erlebe. Daher muss ich keine zusätzliche Entität setzen – insbesondere keine mit solch bemerkenswerten Eigenschaften.Mit anderen Worten: Ich glaube einfach an einen Kreis weniger als Mathematiker. Das ist alles, was erforderlich ist, um zu dem Schluss zu kommen, dass pi eine rationale Zahl für einen bestimmten Kreis ist.
Nur eine Abstraktion!
Ich habe einige Mathematiker behaupten hören, dass geometrische Objekte bloße Abstraktionen sind und daher von der vorhergehenden Kritik ausgenommen sind. Aber das bringt unter anderem die Metaphysik der Abstraktion nach hinten. Sie abstrahieren von Beton. Sie unterscheiden sich nicht vom Abstrakten.
Denken Sie darüber nach. Von was abstrahiert man, um das Konzept eines „perfekten Kreises“ zu erhalten?
Es können nicht die Kreise sein, die wir tatsächlich sehen, da jeder dieser Kreise unvollkommene Kanten hat. Alle konkreten Erfahrungen, die wir machen, bestehen aus Formen mit unvollkommenen Kanten, einem rationalen Pi und bestehen aus Punkten mit Dimensionen. Aus diesen Erfahrungen sagt der Mathematiker: „Nun, ich denke, ein wahrer Kreis ist einer ohne Kanten, mit einem irrationalen pi und besteht aus nulldimensionalen Punkten!“
Das ist Unsinn, und so funktioniert Abstraktion nicht.
Stellen Sie sich vor, wir sprechen über Häuser und abstrakte Vorstellungen von Häusern.
Jedes Haus, dem wir je begegnet sind, hat Wände, einen Boden und eine Decke. Der Mathematiker möchte sagen, dass seine Vorstellung von einem „perfekten Haus“ eines ohne Wände, Böden oder Decke ist. Und tatsächlich sind normale alte Häuser nur Annäherungen an sein perfektes Haus. Offensichtlich ist dies ein Fehler.Wir können eine vollkommen gültige abstrakte Vorstellung von einem Haus haben, aber die Eigenschaften unseres „abstrakten Hauses“ müssen die Eigenschaften der konkreten Häuser einschließen, von denen wir abstrahieren. Unser „geistiges Haus“ muss die konzeptionellen Kategorien „Wände haben, Böden, und eine Decke.“ Die Dimensionen dieser Eigenschaften sind irrelevant, solange sie existieren.Eine abstrakte Vorstellung von „einem Haus ohne Wände, Böden oder Decke“ kann keine Phänomene erklären, die wir erleben, weil sie nichts beschreibt, was möglicherweise existieren könnte. Stellen Sie sich vor, Ihr Freund bringt Sie zu einem leeren Feld und sagt: „Hier ist mein perfektes Haus! Es hat keine Wände, Böden oder eine Decke!“ Man könnte meinen, er sei verrückt – besonders wenn er hinzufügte: „Und alle anderen Häuser sind nur eine Annäherung daran!“
Nicht echt!
Eine der eher selbstbelastenden Antworten von Mathematikern lautet so: „Aber mathematische Objekte sind nicht real! Sie existieren überhaupt nicht!“ In all meiner Forschung kann ich getrost sagen, dass Mathematik der einzige Bereich des Denkens ist, in dem das Eingeständnis, dass „die Objekte, von denen ich spreche, nicht real sind und nicht existieren“, eine bestimmte Theorie verteidigen soll.
Dieser Fehler ist eine Verschmelzung von Objekten und ihren Referenten. Zum Beispiel, Das Konzept von „mein Haus“ soll sich auf „mein Haus in der Welt“ beziehen.“ Es wäre albern zu sagen: „Mein Haus nimmt keinen Platz ein, weil meine Vorstellung von meinem Haus keinen Platz einnimmt.“
In ähnlicher Weise soll sich die Konzeption eines „Punktes“ auf „eine genaue Position im geometrischen Raum“ beziehen.“ Es wäre ebenso albern zu sagen: „Punkte nehmen keinen geometrischen Raum ein, weil meine Vorstellung von einem Punkt keinen geometrischen Raum einnimmt.“Das grundlegende Wesen der Geometrie ist der Raum – ob physischer Raum, mentaler Raum, konzeptueller Raum oder jede andere Art von Raum. Daher müssen die Objekte der Geometrie selbst Platz einnehmen. Es gibt nicht so etwas wie „einen genauen Ort im Raum, der kein genauer Ort im Raum ist.“
Eine alternative Theorie
Lassen Sie mich also einen alternativen geometrischen Rahmen vorstellen. Dies ist nur der Anfang einer ganz neuen Theorie der Mathematik, die ich „Basiseinheit Mathematik“ nenne.“ Dies sind die Grundlagen der Basiseinheitsgeometrie:
1) Alle geometrischen Strukturen bestehen aus Basiseinheiten. Diese Einheiten werden als „Punkte“ bezeichnet.“
2) Jeder Punkt ist räumlich ausgedehnt.
3) In jedem konzeptionellen Rahmen ist die Erweiterung der Basiseinheit genau 1. Innerhalb dieses Rahmens gibt es per Definition keine kleinere Entfernungseinheit.
4) Alle Abstände und Formen können in Bezug auf die Basiseinheit angegeben werden.
Diese Fundamente bilden eine logisch fundierte Grundlage, auf der Geometrie aufgebaut werden kann.
Setzen Sie Punkte zusammen, und Sie können jede beliebige Form ohne irrationale Zahlen zusammenstellen. Jedes Objekt außer der Basiseinheit ist ein zusammengesetztes Objekt, das aus diskreten Punkten besteht. Deshalb habe ich vorhin gesagt, dass ich Euklids ursprüngliche Definition eines „Punktes“ als „das, was keinen Teil hat“ mag.“ Basiseinheiten haben keine Teile; sie sind die Teile, die jedes andere Ganze bilden.
Ich erkenne an, dass es viele Einwände gegen diese Art des Denkens über Geometrie geben wird. Diese Einwände werden in zukünftigen Artikeln ausführlich behandelt.
Um eine Intuition über dieses Framework zu gewinnen, können Sie sich „Punkte“ als „Pixel“ vorstellen, mit denen wir alle Erfahrung haben. Alle Formen und Objekte, denen Sie in einer hochauflösenden VR-Simulation begegnen könnten, sind tatsächlich Klumpen von Pixeln, obwohl sie aus unserer makroskopischen Perspektive „perfekt glatt“ erscheinen könnten.
Ein paar der schönen Implikationen dieser Theorie:
Dies ist eine Linie:

Dies ist ein Kreis:

Und es hat einen nachweislich rationalen pi:
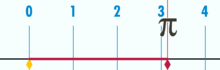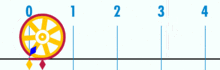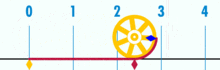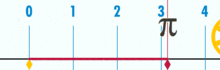
(Hinweis: Dieses GIF wurde aus Wikipedia entnommen, um die angebliche Irrationalität von Pi zu zeigen. Wenn Sie sich jedoch dessen bewusst sind, was Sie gerade sehen, ist dies tatsächlich eine Demonstration der Rationalität von pi. Sie sehen ein GIF der logischen Perfektion und Präzision der Basiseinheitsgeometrie!)
Wie ist das Verhältnis von Umfang zu Durchmesser dieses Kreises? Einfach: Es ist eine ganze Zahl über eine andere – wie viele Basiseinheiten auch immer den Umfang ausmachen, geteilt durch wie viele Einheiten auch immer den Durchmesser ausmachen. Und solange der Kreis nicht aus einer winzigen Menge von Basiseinheiten aufgebaut ist, werden die Pi-Verhältnisse auf etwa 3 funktionieren.14159 (Wenn wir jedoch vollkommen präzise sind, müssen wir in Brüchen angeben, da die dezimale Erweiterung innerhalb eines Basiseinheitsrahmens zweifelhaft sein kann. Aber das ist ein zukünftiger Artikel.). Es gibt keinen „generischen“ oder „idealen“ Kreis. Es gibt konkrete, tatsächliche Kreise, von denen jeder ein zusammengesetztes Objekt ist, das aus einer endlichen Anzahl von Punkten besteht.
Dies bedeutet unter anderem auch, dass es keinen „Einheitskreis“ gibt – einen vermeintlichen Kreis mit einem Radius von 1. Es gibt keine Durchmesser, die einen Abstand von 1 haben. Sie können keinen Kreis mit nur einem Pixel erstellen.
Innerhalb dieser Theorie sind „Kreise“ genau das, was Sie angetroffen haben. „Punkte“ sind Orte im Raum, die tatsächliche Orte im Raum sind, und „Linien“ sind das, was jeder weiß, dass sie sind.Offensichtlich erfordert dieses Thema viel mehr Erklärung und Arbeit, nicht nur in der Geometrie, sondern überall dort, wo die Metaphysik der Mathematik falsch ist. Ich kann nicht alle Einwände gegen die Geometrie der Basiseinheit in diesem Artikel behandeln, aber ich werde ein paar weitere Denkweisen darüber erklären und warum es der Standardorthodoxie überlegen ist.
Zuallererst erklärt dieser Rahmen alle Phänomene, die wir erleben, vollständig und verliert im Vergleich zur Standardgeometrie genau null Erklärungskraft. Jede Form, jeder Kreis, jede Linie, jeder Punkt, jede räumliche Erfahrung, die wir jemals haben werden, kann erklärt werden, ohne die Existenz zusätzlicher Entitäten zu postulieren. Wir erleben keine perfekten Kreise; Deshalb haben wir keinen Grund, über sie zu theoretisieren.
Darüber hinaus ist die Mathematik der Basiseinheiten logischer präziser als die Orthodoxie. Jeder, der mit „irrationalem pi“ gearbeitet hat, muss Näherungen verwenden. Sie können keine tatsächliche unendliche Dezimalerweiterung verwenden. Sie sind gezwungen, die Magnitude für pi willkürlich abzuschneiden, um sie zu verwenden. Nicht so bei der Geometrie der Basiseinheit. Perfekte Präzision ist tatsächlich möglich, da es keine Annäherungen oder unendlichen Dezimalerweiterungen gibt. Dies mag im Moment keine große Sache sein, aber wenn sich die Technologie den Abmessungen der Basiseinheit des physischen Raums nähert, könnte dies tatsächlich einen großen Unterschied machen.
Hier ist eine kurze, interessante Seite über die unendliche Dezimalerweiterung von pi:
Was passiert, wenn orthodoxe Mathematiker immer weitere Dezimalzahlen von pi berechnen? Greifen sie nach den „wahren Verhältnissen des perfekten Kreises“? Nein. Sie berechnen die Pi-Verhältnisse für Kreise mit immer kleineren Basiseinheiten. Wenn die Basiseinheit schrumpft – oder wenn der Kreis im Durchmesser größer wird – ändert sich das Verhältnis von Umfang zu Durchmesser immer geringfügig. Diese Berechnungen sind sofort praktisch, genauso wie Triggertabellen praktisch sind. Sie sind vorberechnete Werte, die für einen bestimmten Kreis einer bestimmten Größe anwendbar und genau sind.
(Wenn Sie verstehen wollen, warum sich pi leicht ändert, denken Sie so: Wenn die Größe der Basiseinheit zunimmt, schrumpft die vom Umfang umschlossene Fläche; Wenn die Größe der Basiseinheit abnimmt, nimmt die vom Umfang umschlossene Fläche zu, jedoch mit abnehmender Geschwindigkeit. Je glatter der Rand des Kreises ist, desto größer ist die Fläche des Kreises.)
Zu diesem Hinweis: Die Geometrie der Basiseinheit erfordert keine „ultimative Basiseinheit.“ Mit anderen Worten, jedes konzeptionelle Schema wird aus logischer Notwendigkeit eine Basiseinheit haben, aber das bedeutet nicht, dass Sie daran gehindert werden, ein anderes konzeptionelles Schema mit einer kleineren Basiseinheit zu entwickeln.
Stellen Sie es sich so vor: Jedes gegebene Foto enthält eine endliche Anzahl von Pixeln. Es wird eine Basiseinheit Auflösung haben. Dies bedeutet jedoch nicht, dass es unmöglich ist, ein Foto mit höherer Auflösung aufzunehmen. In ähnlicher Weise hat jeder Kreis eine Auflösung der Basiseinheit, aber das bedeutet nicht, dass es unmöglich ist, sich eine mit höherer Auflösung (kleinere Basiseinheiten) vorzustellen.
Wir könnten sogar an die Grenzen der physischen Welt stoßen. Der physische Raum muss eine Basiseinheit haben, was bedeutet, dass es innerhalb unseres physischen Systems keine kleinere Einheit gibt. Dies bedeutet jedoch nicht, dass wir daran gehindert werden, über kleindimensionale Basiseinheiten zu sprechen. Diese Objekte korrelieren einfach nicht mit unserem Universum. Wer weiß – vielleicht könnten wir wahre Dinge über ein anderes physisches Universum sagen, das kleinere Basiseinheiten hat.
Hinweis: Dies korreliert auch perfekt mit meiner Auflösung von Zenos Paradoxien. Der Raum muss eine Basiseinheit haben, wenn Bewegung möglich ist.
Ein gutes Beispiel für Phänomene der Basiseinheit ist das Fraktal. Angeblich machen Fraktale nur im konzeptionellen Rahmen der „unendlichen Teilbarkeit“ Sinn.“ Das ist nicht korrekt. Fraktale sind in einem Basiseinheitskontext viel sinnvoller. Betrachten Sie dieses Bild:

Dies sieht aus wie ein Hauptkandidat für „unendliche Teilbarkeit.“ Es ist jedoch eine Illusion. Zu jedem Zeitpunkt gibt es eine Basiseinheit Auflösung zu diesem Bild. Wenn das Bild „vergrößert“ wird, werden neue Einheiten erstellt, die alle in Pixeln angegeben sind. Zu keinem Zeitpunkt schauen Sie in die Unendlichkeit; Sie schauen immer auf eine endliche Anzahl von Pixeln. Wenn Sie dies bezweifeln, können Sie die Pixel zählen. Das Objekt wird so konstruiert, wie Sie es sehen. Das Gleiche passiert in der Mathematik; Die Objekte werden so konstruiert, wie man sie sich vorstellt. Darüber wird in zukünftigen Artikeln noch viel mehr gesagt.
Polygone und Griechen
Ich möchte schnell einen Einwand ansprechen, der unweigerlich aufkommen wird – diejenigen, die behaupten, dass die Bilder von Kreisen in diesem Artikel eigentlich keine Kreise sind; Sie sind Polygone. Die Kanten sind ein paar kleine gerade Linien; sie sind nicht perfekt glatt. Wenn dies zutrifft, ist es keine Kritik an der Geometrie der Basiseinheit, da alle runden Objekte, denen wir begegnen, Polygone wären. Daher sollten unsere mathematischen Theorien über Polygone sein; wir erfahren nichts anderes. Ich möchte etwas über die Eigenschaften dieser Form wissen:

Es ist mir egal, wie du es nennst. Die Basiseinheitsgeometrie kann Sie über die Eigenschaften dieser Form informieren.
Diesen Fehler machten auch die Griechen, wenn sie von Kreisen sprachen – als wären sie aus einer „unendlichen Anzahl von Linien“ aufgebaut.“ Das ist falsch. Kreise und Polygone bestehen aus einer endlichen Anzahl von Punkten, nicht aus Linien. Linien bilden nichts; sie sind selbst zusammengesetzte Objekte.
Stellen Sie sich vor, Sie bauen einen Kreis im Sand.

Wie groß ist dieser Kreis? Ich garantiere, es ist eine endliche, rationale Zahl. Sie können buchstäblich die Sandkörner zählen, aus denen es besteht. Der Umfang besteht aus Sandkörnern, ebenso wie der Durchmesser und die Fläche. Sie sind alle ganze Zahlen.
Das letzte Argument, das ich in diesem Artikel ansprechen werde, wird von denen kommen, die denken, dass ein „Kreis“ keine Form ist; es ist ein mathematischer Ausdruck. So etwas wie (x2 + y2 = r2).
Dies ist nur eine weitere metaphysische Verwirrung, die Symbole mit dem Objekt verbindet, das die Symbole beschreiben sollen. Es ist, als würde man sagen: „Äpfel sind gleichbedeutend mit den Worten“eine rote Frucht.“ Das ist verwirrt. Die Worte „eine rote Frucht“ sind eine Beschreibung des Objekts, nicht das Objekt selbst. Die Formel like (x2 + y2 = r2) beschreibt die Form eines Kreises – oder, wenn Sie es vorziehen, so darüber nachzudenken – es ist eine Regel für die Konstruktion eines Kreises. Es ist nicht selbst ein Kreis.
An dieser Stelle beende ich diesen Artikel. In Zukunft gibt es noch viel mehr zu sagen. Mathematik ist nicht frei von Kritik oder skeptischer Untersuchung. Es ist auch nicht von der Notwendigkeit einer präzisen Metaphysik befreit. Aus all den Gründen, die ich in diesem Beitrag skizziert habe, gibt es viel Raum für alternative – und überlegene – Vorstellungen von Geometrie. Die Geometrie der Basiseinheit verliert keine Erklärungskraft, beseitigt eine unendliche Anzahl unnötiger Objekte und bietet eine logische Grundlage, auf der eine stärkere Theorie aufgebaut werden kann.Wenn Sie nicht an die Existenz von „perfekten Kreisen“ glauben – die aus unendlich vielen nulldimensionalen Punkten bestehen -, dann glauben Sie nicht, dass pi irrational ist, und Sie haben sich einer extrem kleinen Gruppe von intellektuellen Leprakranken angeschlossen. Sie können jetzt Spott und Verurteilung für Ihre Häresie erwarten.
Wenn Ihnen dieser Artikel gefallen hat und Sie die Schaffung von mehr Häresie unterstützen möchten, besuchen Sie patreon.com/stevepatterson .