BasicsEdit
Zunächst einige Vokabeln:
| Aktivierung | = Zustandswert des Neurons. Für binäre Neuronen ist dies normalerweise 0 / 1 oder +1 / -1. |
| CAM | = Inhalt adressierbaren Speicher. Abrufen eines Speichers durch ein Teilmuster anstelle einer Speicheradresse. |
| Konvergenz | = die Stabilisierung eines Aktivierungsmusters in einem Netzwerk. In SL bedeutet Konvergenz die Stabilisierung von Gewichten & Verzerrungen anstelle von Aktivierungen. |
| diskriminativ | = in Bezug auf Erkennungsaufgaben. Auch Analyse (in der Mustertheorie) oder Inferenz genannt. |
| Energie | = eine makroskopische Größe, die das Aktivierungsmuster in einem Netzwerk beschreibt. (siehe unten) |
| Generalisierung | = genaues Verhalten bei zuvor nicht angetroffenen Eingaben |
| generative | = Maschinelles Lernen und Rückruf. manchmal auch Synthese (in der Mustertheorie), Mimikry oder Deep Fakes genannt. |
| Inferenz | = die „Run“ -Phase (im Gegensatz zum Training). Während der Inferenz führt das Netzwerk die Aufgabe aus, für die es trainiert wurde — entweder ein Muster erkennen (SL) oder eines erstellen (UL). Normalerweise steigt die Inferenz den Gradienten einer Energiefunktion ab. Im Gegensatz zu SL tritt Gradientenabstieg während des Trainings auf, NICHT Inferenz. |
| Bildverarbeitung | = maschinelles Lernen auf Bildern. |
| NLP | = Verarbeitung natürlicher Sprache. Maschinelles Lernen menschlicher Sprachen. |
| Muster | = Netzwerkaktivierungen, die in gewissem Sinne eine interne Reihenfolge haben oder die durch Merkmale in den Aktivierungen kompakter beschrieben werden können. Beispielsweise weist das Pixelmuster einer Null, unabhängig davon, ob es als Daten angegeben oder vom Netzwerk vorgestellt wird, ein Merkmal auf, das als einzelne Schleife beschrieben werden kann. Die Merkmale sind in den versteckten Neuronen codiert. |
| training | = die Lernphase. Hier passt das Netzwerk seine Gewichtungen & an, um von den Eingaben zu lernen. |
Aufgaben
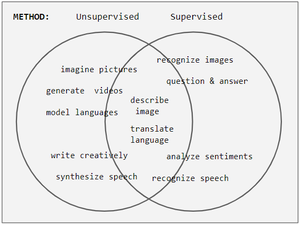
UL-Methoden bereiten ein Netzwerk normalerweise eher auf generative Aufgaben als auf die Erkennung vor, aber das Gruppieren von Aufgaben als überwacht oder nicht kann verschwommen sein. Zum Beispiel begann die Handschrifterkennung in den 1980er Jahren als SL. Im Jahr 2007 wird UL verwendet, um das Netzwerk für SLA vorzubereiten. Derzeit hat SL seine Position als bessere Methode wiedererlangt.
Training
Während der Lernphase versucht ein unüberwachtes Netzwerk, die ihm gegebenen Daten nachzuahmen, und verwendet den Fehler in seiner nachgeahmten Ausgabe, um sich selbst zu korrigieren (z. seine Gewichte & Verzerrungen). Dies ähnelt dem Mimikry-Verhalten von Kindern, wenn sie eine Sprache lernen. Manchmal wird der Fehler als eine geringe Wahrscheinlichkeit ausgedrückt, dass die fehlerhafte Ausgabe auftritt, oder er kann als instabiler Hochenergiezustand im Netzwerk ausgedrückt werden.
Energie
Eine Energiefunktion ist ein makroskopisches Maß für den Zustand eines Netzwerks. Diese Analogie zur Physik ist inspiriert von Ludwig Boltzmanns Analyse der makroskopischen Energie eines Gases aus den mikroskopischen Wahrscheinlichkeiten der Teilchenbewegung p ∝ {\displaystyle \propto }

eE/kT, wobei k die Boltzmann-Konstante und T die Temperatur ist. Im RBM-Netzwerk ist die Beziehung p = e-E /Z, wobei p & E über jedes mögliche Aktivierungsmuster variiert und Z = ∑ A l l P a t t e r n s {\displaystyle \sum _{AllPatterns}}

e -E(Muster). Genauer gesagt ist p(a) = e-E(a) / Z, wobei a ein Aktivierungsmuster aller Neuronen (sichtbar und verborgen) ist. Daher tragen frühe neuronale Netze den Namen Boltzmann-Maschine. Paul Smolensky nennt -E die Harmonie. Ein Netzwerk sucht niedrige Energie, die hohe Harmonie ist.
Netzwerke
| Hopfield | Boltzmann | RBM | Helmholtz | Autoencoder | VAE |
|---|---|---|---|---|---|
 |
 |
 restricted Boltzmann machine
|
 |
 autoencoder
|
 variational autoencoder
|
Boltzmann und Helmholtz kamen vor neuronalen Netzen Formulierungen, aber diese Netzwerke entlehnt aus ihren Analysen, so dass diese Netzwerke tragen ihre Namen. Hopfield trug jedoch direkt zu UL bei.
IntermediateEdit
Hier werden die Verteilungen p(x) und q(x) als p und q abgekürzt.
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) AI winter I |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolution neural network. Es wird hauptsächlich in SL verwendet, verdient aber hier eine Erwähnung. |
| 1982 | Ist eine Variante Hopfield net beschrieben als Nocken und Klassifikatoren von John Hopfield. |
| 1983 | Ist eine Variante der Boltzmann-Maschine mit probabilistischen Neuronen, die von Hinton & Sejnowski nach Sherington & Kirkpatricks Arbeit von 1975 beschrieben wurde. |
| 1986 | Paul Smolensky veröffentlicht Harmony Theory, eine RBM mit praktisch derselben Boltzmann-Energiefunktion. Smolensky gab kein praktisches Ausbildungsprogramm. Hinton tat dies Mitte der 2000er Jahre |
| 1995 | Schmidthuber stellt das LSTM-Neuron für Sprachen vor. |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) AI winter II |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Some more vocabulary:
| Wahrscheinlichkeit | |
| cdf | = kumulative Verteilungsfunktion. das Integral des PDF. Die Wahrscheinlichkeit, sich 3 zu nähern, ist die Fläche unter der Kurve zwischen 2,9 und 3,1. |
| kontrastive Divergenz | = eine Lernmethode, bei der man die Energie auf Trainingsmuster senkt und die Energie auf unerwünschte Muster außerhalb des Trainingssatzes erhöht. Dies unterscheidet sich stark von der KL-Divergenz, hat aber einen ähnlichen Wortlaut. |
| erwarteter Wert | = E(x) = ∑ x {\displaystyle \sum _{x}}
 x * p(x). Dies ist der Mittelwert oder Durchschnittswert. Ersetzen Sie für den kontinuierlichen Eingang x die Summation durch ein Integral. |
| latente Variable | = eine unbeobachtete Größe, die hilft, beobachtete Daten zu erklären. zum Beispiel kann eine Grippeinfektion (unbeobachtet) erklären, warum eine Person niest (beobachtet). In probabilistischen neuronalen Netzen fungieren versteckte Neuronen als latente Variablen, obwohl ihre latente Interpretation nicht explizit bekannt ist. |
| = Wahrscheinlichkeitsdichtefunktion. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen bestimmten Wert annimmt. Für kontinuierliches pdf kann p (3) = 1/2 immer noch bedeuten, dass die Chance nahe Null ist, diesen genauen Wert von 3 zu erreichen. Wir rationalisieren dies mit der cdf. | |
| stochastic | = verhält sich nach einer gut beschriebenen Wahrscheinlichkeitsdichteformel. |
| Thermodynamics | |
| Boltzmann distribution | = Gibbs distribution. p ∝ {\displaystyle \propto }
 eE/kT |
| entropy | = expected information = ∑ x {\displaystyle \sum _{x}}
 p * log p |
| Gibbs free energy | = thermodynamic potential. Es ist die maximale reversible Arbeit, die von einem Wärmesystem bei konstanter Temperatur und konstantem Druck ausgeführt werden kann. freie Energie G = Wärme – Temperatur * Entropie |
| Information | = die Informationsmenge einer Nachricht x = -log p(x) |
| KLD | = relative Entropie. Für probabilistische Netzwerke ist dies das Analogon des Fehlers zwischen input & imitierter Ausgabe. Die Kullback-Liebler-Divergenz (KLD) misst die Entropieabweichung von 1 Verteilung von einer anderen Verteilung. KLD(p,q) = ∑ x {\displaystyle \Summe _{x}}
 p * log( p / q ). Typischerweise spiegelt p die Eingabedaten wider, q spiegelt die Interpretation des Netzwerks wider und KLD spiegelt den Unterschied zwischen den beiden wider. |
Vergleich von Netzwerken
| Hopfield | Boltzmann | RBM | Helmholtz | Autoencoder | VAE | |
|---|---|---|---|---|---|---|
| Verwendung & notables | CAM, reisender Verkäufer Problem | CAM. Die Freiheit der Verbindungen macht es schwierig, dieses Netzwerk zu analysieren. | Mustererkennung (MNIST, Spracherkennung) | imagination, Mimikry | Sprache: kreatives Schreiben, Übersetzung. Vision: verbesserung verschwommener Bilder | Generieren Sie realistische Daten |
| neuron | deterministischer binärer Zustand. Aktivierung = { 0 (oder -1) wenn x negativ ist, 1 sonst } | stochastische Binärdatei Hopfield neuron | stochastische Binärdatei. Erweitert auf Realwert Mitte der 2000er Jahre | binär, sigmoid | Sprache: LSTM. vision: lokale rezeptive Felder. in der regel real bewertet relu Aktivierung. | |
| Verbindungen | 1-Schicht mit symmetrischen Gewichten. Keine Selbstverbindungen. | 2-lagig. 1-versteckt & 1-sichtbar. symmetrische Gewichte. | 2-lagig. symmetrische Gewichte. keine seitlichen Verbindungen innerhalb einer Schicht. | 3-Lagen: asymmetrische Gewichte. 2 netzwerke zu 1 zusammengefasst. | 3-lagig. Die Eingabe wird als Layer betrachtet, obwohl sie keine eingehenden Gewichtungen aufweist. wiederkehrende Schichten für NLP. feedforward windungen für vision. input & Ausgabe haben die gleichen Neuronenzahlen. | 3-schichten: eingang, encoder, verteilung sampler decoder. der Sampler wird nicht als Schicht betrachtet (e) |
| Inferenz & Energie | Energie wird durch Gibbs-Wahrscheinlichkeitsmaß gegeben : E = − 1 2 ∑ i , j w i j s i s j + ∑ i θ i s i {\displaystyle E=-{\frac {1}{2}}\Summe _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\Summe _{i}{\theta _{i}}{s_{i}}}
 |
← same | ← same | AME Divergenz minimieren | Inferenz ist nur Feed-Forward. vorherige UL-Netzwerke liefen vorwärts UND rückwärts | Minimierungsfehler = Rekonstruktionsfehler – KLD |
| Training | Δwij = si*sj, für +1 / -1 Neuron | Δwij = e*(pij – p’ij). Dies wird von der KLD abgeleitet. e = Lernrate, p‘ = vorhergesagte und p = tatsächliche Verteilung. | kontrastive Divergenz mit Gibbs-Sampling | Wake-Sleep 2-Phasen-Training | zurück propagieren Sie den Rekonstruktionsfehler | Parametrisieren Sie den versteckten Zustand für backprop |
| Stärke | ähnelt physikalischen Systemen, so dass sie ihre Gleichungen erben | <— gleich. versteckte Neuronen fungieren als interne Repräsentation der Außenwelt | schnelleres praktischeres Trainingsprogramm als Boltzmann-Maschinen | leicht anatomisch. analysierbar mit Informationstheorie & Statistische Mechanik | ||
| Schwäche | hopfield | schwer zu trainieren durch seitliche Verbindungen | RBM | Helmholtz |
Spezifische Netzwerke
Hier heben wir einige Merkmale der einzelnen Netzwerke hervor. Ferromagnetismus inspirierte Hopfield-Netzwerke, Boltzmann-Maschinen und RBMs. Ein Neuron entspricht einer Eisendomäne mit binären magnetischen Momenten nach oben und unten, und neuronale Verbindungen entsprechen dem Einfluss der Domäne aufeinander. Symmetrische Verbindungen ermöglichen eine globale Energieformulierung. Während der Inferenz aktualisiert das Netzwerk jeden Status mit der Standard-Aktivierungsschrittfunktion. Symmetrische Gewichte garantieren Konvergenz zu einem stabilen Aktivierungsmuster.
Hopfield-Netzwerke werden als CAMs verwendet und sind garantiert zu einem bestimmten Muster zu begleichen. Ohne symmetrische Gewichte ist das Netzwerk sehr schwer zu analysieren. Mit der richtigen Energiefunktion konvergiert ein Netzwerk.Boltzmann-Maschinen sind stochastische Hopfield-Netze. Ihr Zustandswert wird aus diesem PDF wie folgt abgetastet: Angenommen, ein binäres Neuron feuert mit der Bernoulli-Wahrscheinlichkeit p (1) = 1/3 und ruht auf p (0) = 2/3. Man nimmt Proben davon, indem man eine GLEICHMÄßIG verteilte Zufallszahl y nimmt und sie in die invertierte kumulative Verteilungsfunktion einfügt, die in diesem Fall die Schrittfunktion ist, die bei 2/3 liegt. Die inverse Funktion = { 0 if x <= 2/3, 1 if x > 2/3 }
Helmholtz-Maschinen sind frühe Inspirationen für die Variations-Auto-Encoder. Es sind 2 Netzwerke, die zu einem zusammengefasst sind – Vorwärts-Gewichte funktionieren, und Rückwärts-Gewichte implementieren die Vorstellungskraft. Es ist vielleicht das erste Netzwerk, das beides tut. Helmholtz arbeitete nicht im maschinellen Lernen, aber er inspirierte die Ansicht der „statistischen Inferenz-Engine, deren Funktion es ist, wahrscheinliche Ursachen für sensorischen Input abzuleiten“ (3). das stochastische binäre Neuron gibt eine Wahrscheinlichkeit aus, dass sein Zustand 0 oder 1 ist. Die Dateneingabe wird normalerweise nicht als Schicht betrachtet, aber im Generierungsmodus der virtuellen Maschine erhält die Datenschicht eine Eingabe von der mittleren Schicht, die zu diesem Zweck separate Gewichtungen aufweist, sodass sie als Schicht betrachtet wird. Daher hat dieses Netzwerk 3 Schichten.Variational Autoencoder (VAE) sind von Helmholtz-Maschinen inspiriert und kombiniert Wahrscheinlichkeitsnetzwerke mit neuronalen Netzen. Ein Autoencoder ist ein 3-Schicht-CAM-Netzwerk, bei dem die mittlere Schicht eine interne Darstellung von Eingabemustern sein soll. Die Gewichte heißen phi & theta und nicht W und V wie in Helmholtz — ein kosmetischer Unterschied. Das neuronale Kodierernetzwerk ist eine Wahrscheinlichkeitsverteilung qφ (z|x) und das Dekodierernetzwerk ist pθ (x|z). Diese 2 Netzwerke können hier vollständig verbunden sein oder ein anderes NN-Schema verwenden.
Hebbian Learning, ART, SOM
Das klassische Beispiel für unbeaufsichtigtes Lernen bei der Untersuchung neuronaler Netze ist Donald Hebbs Prinzip, dh Neuronen, die zusammen feuern, verdrahten sich. Beim Hebbischen Lernen wird die Verbindung unabhängig von einem Fehler verstärkt, sondern ist ausschließlich eine Funktion der Koinzidenz zwischen Aktionspotentialen zwischen den beiden Neuronen. Eine ähnliche Version, die synaptische Gewichte modifiziert, berücksichtigt die Zeit zwischen den Aktionspotentialen (Spike-Timing-dependent plasticity oder STDP). Es wurde die Hypothese aufgestellt, dass Hebbisches Lernen einer Reihe kognitiver Funktionen wie Mustererkennung und Erfahrungslernen zugrunde liegt.
Unter den neuronalen Netzwerkmodellen werden die selbstorganisierende Karte (SOM) und die adaptive Resonanztheorie (ART) häufig in unbeaufsichtigten Lernalgorithmen verwendet. Das SOM ist eine topografische Organisation, in der nahe gelegene Orte in der Karte Eingaben mit ähnlichen Eigenschaften darstellen. Das ART-Modell ermöglicht es, die Anzahl der Cluster mit der Problemgröße zu variieren, und ermöglicht es dem Benutzer, den Ähnlichkeitsgrad zwischen Mitgliedern desselben Clusters mithilfe einer benutzerdefinierten Konstante zu steuern, die als Vigilanzparameter bezeichnet wird. ART-Netzwerke werden für viele Mustererkennungsaufgaben wie die automatische Zielerkennung und die seismische Signalverarbeitung verwendet.