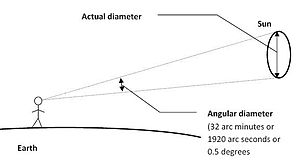
In der Astronomie werden die Größen von Himmelsobjekten oft in Bezug auf ihren Winkeldurchmesser von der Erde aus gesehen und nicht in Bezug auf ihre tatsächliche Größe angegeben. Da diese Winkeldurchmesser typischerweise klein sind, ist es üblich, sie in Bogensekunden („) darzustellen. Eine Bogensekunde ist 1/3600 eines Grades (1°) und ein Bogenmaß ist 180/ π {\displaystyle \pi }

Grad. Ein Bogenmaß entspricht also 3.600 × 180 / π {\displaystyle \pi }

Bogensekunden, was etwa 206.265 Bogensekunden entspricht (1 rad ≈ 206.264,806247 „). Daher ist der Winkeldurchmesser eines Objekts mit dem physikalischen Durchmesser d in einem Abstand D, ausgedrückt in Bogensekunden, gegeben durch: δ = 206, 265 ( d /D ) a r c s e c o n d s {\displaystyle \delta =206,265~(d/D)~\mathrm {arcseconds} }

.
Diese Objekte haben einen Winkeldurchmesser von 1″:
- ein Objekt mit einem Durchmesser von 1 cm in einer Entfernung von 2,06 km
- ein Objekt mit einem Durchmesser von 725,27 km in einer Entfernung von 1 astronomischen Einheit (AU)
- ein Objekt mit einem Durchmesser von 45 866 916 km bei 1 Lichtjahr
- ein Objekt mit einem Durchmesser von 1 AU (149 597 871 km) in einer Entfernung von 1 parsec (pc)
Somit, der Winkeldurchmesser der Erdumlaufbahn um die Sonne aus einer Entfernung von 1 pc beträgt 2 „, da 1 AU der mittlere Radius der Erdumlaufbahn ist.
Der Winkeldurchmesser der Sonne aus einer Entfernung von einem Lichtjahr beträgt 0,03 „und der der Erde 0,0003 „. Der Winkeldurchmesser 0.03“ der oben angegebenen Sonne ist ungefähr die gleiche wie die eines menschlichen Körpers in einem Abstand des Durchmessers der Erde.
Diese Tabelle zeigt die Winkelgrößen der Himmelskörper von der Erde aus gesehen:
| Himmelskörper | Winkeldurchmesser oder Größe | Relative Größe |
|---|---|---|
| Andromeda-Galaxie | 3 °10 ‚ x 1° | Etwa sechsmal so groß wie die Sonne oder der Mond. Nur der viel kleinere Kern ist ohne Langzeitbelichtung sichtbar. |
| Sun | 31′27″ – 32′32″ | 30–31 times the maximum value for Venus (orange bar below) / 1887–1952″ |
| Moon | 29′20″ – 34′6″ | 28–32.5 times the maximum value for Venus (orange bar below) / 1760–2046″ |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 9.7″ – 1′6″ | |
| Jupiter | 29.8″ – 50.1″ | |
| Saturn | 14.5″ – 20.1″ | |
| Mars | 3.5″ – 25.1″ | |
| Mercury | 4.5″ – 13.0″ | |
| Uranus | 3.3″ – 4.1″ | |
| Neptune | 2.2″ – 2.4″ | |
| Ceres | 0.33″ – 0.84″ | |
| Vesta | 0.20″ – 0.64″ | |
| Pluto | 0.06″ – 0.11″ | |
| R Doradus | 0.052″ – 0.062″ | |
| Betelgeuse | 0.049″ – 0.060″ | |
| Eris | 0.034″ – 0.089″ | |
| Alphard | 0.00909″ | |
| Alpha Centauri A | 0.007″ | |
| Canopus | 0.006″ | |
| Sirius | 0.005936″ | |
| Altair | 0.003″ | |
| Deneb | 0.002″ | |
| Proxima Centauri | 0.001″ | |
| Alnitak | 0.0005″ | |
| Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019. | 0.000025″
(2.5×10-5) |
|
| Ein Stern wie Alnitak in einer Entfernung, in der das Hubble-Weltraumteleskop ihn nur sehen könnte | 6×10-10 Bogensekunden |


Die Tabelle zeigt, dass der Winkeldurchmesser der Sonne von der Erde aus gesehen ungefähr 32′ (1920 “ oder 0,53 °) beträgt, wie oben dargestellt.
Somit ist der Winkeldurchmesser der Sonne etwa 250.000 mal so groß wie der von Sirius. (Sirius hat den doppelten Durchmesser und seine Entfernung ist 500.000 mal so groß; Die Sonne ist 1010 mal so hell, was einem Winkeldurchmesserverhältnis von 105 entspricht, also ist Sirius ungefähr 6 mal so hell pro Raumwinkeleinheit.)
Der Winkeldurchmesser der Sonne ist auch etwa 250.000 mal so groß wie der von Alpha Centauri A (es hat ungefähr den gleichen Durchmesser und der Abstand ist 250.000 mal so groß; die Sonne ist 4 × 1010 mal so hell, was einem Winkeldurchmesserverhältnis von 200.000 entspricht, also ist Alpha Centauri A pro Raumwinkeleinheit etwas heller).
Der Winkeldurchmesser der Sonne ist ungefähr der gleiche wie der des Mondes. (Der Durchmesser der Sonne ist 400 mal so groß und seine Entfernung auch; Die Sonne ist 200.000 bis 500.000 mal so hell wie der Vollmond (Zahlen variieren), entsprechend einem Winkeldurchmesserverhältnis von 450 bis 700, so dass ein Himmelskörper mit einem Durchmesser von 2,5–4 „und der gleichen Helligkeit pro Raumwinkeleinheit die gleiche Helligkeit wie der Vollmond hätte.Obwohl Pluto physikalisch größer ist als Ceres, hat Ceres von der Erde aus gesehen (z. B. durch das Hubble-Weltraumteleskop) eine viel größere scheinbare Größe.
In Grad gemessene Winkelgrößen sind nützlich für größere Himmelsflecken. (Zum beispiel, die drei sterne der Gürtel abdeckung über 4,5 ° von winkel größe.) Jedoch werden viel feinere Einheiten benötigt, um die Winkelgrößen von Galaxien, Nebeln oder anderen Objekten des Nachthimmels zu messen.
Grad werden daher wie folgt unterteilt:
- 360 Grad (°) in einem Vollkreis
- 60 Bogenminuten (‚) in einem Grad
- 60 Bogensekunden („) in einer Bogenminute
Um dies relativieren zu können, beträgt der Vollmond von der Erde aus gesehen etwa 1 ⁄ 2 ° oder 30′ (oder 1800″). Die Bewegung des Mondes über den Himmel kann in Winkelgröße gemessen werden: ungefähr 15 ° pro Stunde oder 15 „pro Sekunde. Eine eine Meile lange Linie, die auf das Gesicht des Mondes gemalt ist, scheint von der Erde etwa 1 „lang zu sein.
In der Astronomie ist es normalerweise schwierig, die Entfernung zu einem Objekt direkt zu messen, aber das Objekt kann eine bekannte physikalische Größe (vielleicht ähnelt es einem näheren Objekt mit bekannter Entfernung) und einen messbaren Winkeldurchmesser haben. In diesem Fall kann die Winkeldurchmesserformel invertiert werden, um den Winkeldurchmesserabstand zu entfernten Objekten als zu ergeben
d ≡ 2 D tan ( δ 2 ) {\displaystyle d\equiv 2D\tan \left({\frac {\delta }{2}}\right)}

. Im nicht-euklidischen Raum, wie unserem expandierenden Universum, ist der Winkeldurchmesser Abstand nur eine von mehreren Definitionen der Entfernung, so dass es verschiedene „Entfernungen“ zum selben Objekt geben kann. Siehe Entfernungsmaße (Kosmologie).
Nicht kreisförmige Objektebearbeiten
Viele Deep-Sky-Objekte wie Galaxien und Nebel erscheinen nicht kreisförmig und erhalten daher typischerweise zwei Durchmessermaße: die Hauptachse und die Nebenachse. Zum Beispiel hat die Kleine Magellansche Wolke einen sichtbaren scheinbaren Durchmesser von 5° 20′ × 3° 5′.
Beleuchtungsdefekt
Beleuchtungsdefekt ist die maximale Winkelbreite des unbeleuchteten Teils eines Himmelskörpers, der von einem gegebenen Beobachter gesehen wird. Wenn ein Objekt beispielsweise einen Bogendurchmesser von 40 „hat und zu 75% beleuchtet ist, beträgt der Beleuchtungsfehler 10“.