seuraava: 3.4 jääkaapit ja lämpeneminen: 3. Ensimmäinen laki edellinen: 3.2 yleinen esitys sisällön indeksi
Carnot sykli on esitetty kuvassa 3.4. Sillä on neljä prosessia. Adiabaattisia kääntyviä jalkoja on kaksi ja kääntyviä jalkoja kaksi. Voimme rakentaa Carnot sykli kanssamonet erilaiset järjestelmät, mutta käsitteet voidaan osoittaa käyttämällä tuttavallinen työneste, ideaalikaasu. Järjestelmää voidaan pitää männällä suljettuna kammiona, joka täytetään tällä ideaalikaasulla.
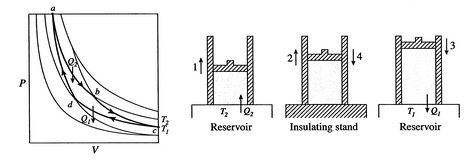
Carnot ’ n syklin neljä prosessia ovat:
- systeemi on lämpötilassa
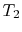 tilassa
tilassa  . Se kiinnitetään kosketukseen lämpövarastoon, joka on vain niin suuri nestemäinen tai Solid massa, että sen lämpötila ei muutu merkittävästi, kun tietty määrä lämpöä siirretään järjestelmään. Toisin sanoen lämpövarasto on jatkuva lämpötilalähde (tai vastaanotin) lämpöä. Tämän jälkeen systeemi laajenee anisotermisesti
. Se kiinnitetään kosketukseen lämpövarastoon, joka on vain niin suuri nestemäinen tai Solid massa, että sen lämpötila ei muutu merkittävästi, kun tietty määrä lämpöä siirretään järjestelmään. Toisin sanoen lämpövarasto on jatkuva lämpötilalähde (tai vastaanotin) lämpöä. Tämän jälkeen systeemi laajenee anisotermisesti 
 , jolloin lämpö absorboituu
, jolloin lämpö absorboituu 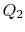 .
. - Atstate
 , järjestelmä on lämpöeristetty (poistettu kontaktista lämpövaraston kanssa) ja sen jälkeen sen annetaan laajentua
, järjestelmä on lämpöeristetty (poistettu kontaktista lämpövaraston kanssa) ja sen jälkeen sen annetaan laajentua  . Tämän ekspansion aikana lämpötila laskee
. Tämän ekspansion aikana lämpötila laskee  . Lämpö vaihtui tämän jakson aikana,
. Lämpö vaihtui tämän jakson aikana, 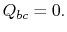 )
) - tilassa
 systeemi on kosketuksissa lämpövarastoon lämpötilassa
systeemi on kosketuksissa lämpövarastoon lämpötilassa  . Se pakataan tilaan
. Se pakataan tilaan 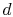 , jolloin heat
, jolloin heat 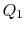 in the process.
in the process. - lopulta järjestelmä pakataan adiabaattisesti takaisin alkutilaan
 . Lämmönsiirto
. Lämmönsiirto 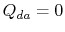 .
.
syklin lämpöhyötysuhde saadaan määritelmällä
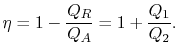 |
(3..4) |
tässä yhtälössä on viittomakäytäntö. Suureet![]()
![]() sellaisina kuin ne on määritelty, ovat absorboituneen lämmön magnitudeja andrejected. Määrät
sellaisina kuin ne on määritelty, ovat absorboituneen lämmön magnitudeja andrejected. Määrät ![]()
![]() puolestaan määritellään järjestelmän vastaanottaman lämmön perusteella. Tässä esimerkissä former on negatiivinen ja jälkimmäinen on positiivinen. Järjestelmän absorboima ja absorboima lämpö tapahtuu isotermisissä prosesseissa, ja tiedämme jo, mitkä niiden arvot ovat Eq: sta.(3.1):
puolestaan määritellään järjestelmän vastaanottaman lämmön perusteella. Tässä esimerkissä former on negatiivinen ja jälkimmäinen on positiivinen. Järjestelmän absorboima ja absorboima lämpö tapahtuu isotermisissä prosesseissa, ja tiedämme jo, mitkä niiden arvot ovat Eq: sta.(3.1):
Theefficiency voidaan nyt kirjoittaa eri tilojen tilavuuksien mukaan seuraavasti:
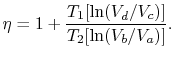 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) showstwo seurauksia. Ensin vastaanotetut ja hylätyt lämmöt suhteutetaan syklin isotermisten osien lämpötiloihin
toiseksi Carnot ’ n syklin hyötysuhteen kertoo kompaktisti

hyötysuhde voi olla 100% vain, jos lämpötila, jossa lämpö hylätään, on nolla. Lämmön ja työn siirrot järjestelmään ja sieltä pois esitetään kaavamaisesti inFigure 3.5.
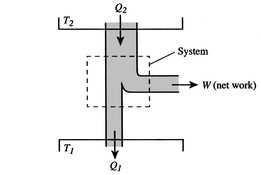
Muddy Points
Since ![]() , kun tarkastellaan
, kun tarkastellaan ![]()
![]() kaavio, tarkoittaako se kauempana toisistaan
kaavio, tarkoittaako se kauempana toisistaan ![]()
![]() isotermit ovatko, suurempi tehokkuus? Ja jos he olisivat hyvin lähellä, se olisi erittäin tehotonta? (MP 3.2)
isotermit ovatko, suurempi tehokkuus? Ja jos he olisivat hyvin lähellä, se olisi erittäin tehotonta? (MP 3.2)
miksi Carnot ’ n syklissä käsitellään vain tilavuusmuutoksia ja ei adiabaattien ja isotermien painemuutoksia?(MP 3.3)
onko Carnot-syklille olemassa fyysinen sovellus? Voimmeko suunnitella Carnot-Moottorin propulsiolaitteeksi?(MP 3.4)
Mistä tiedämme, mitä syklejä käytetään malleina todellisille prosesseille?(MP 3.5)
seuraava: 3.4 jääkaapit ja lämmittäminen: 3. Ensimmäinen Laki Edellinen: 3.2 yleistetty esitys sisällysluettelosta
UnifiedTP