määritelmä
muuttujan x polynomi on funktio, joka voidaan kirjoittaa muotoon
missä An, an-1 , …, a2, a1, a0 ovat vakioita. Kutsumme termiä, joka sisältää suurimman tehon x (eli anxn) johtava termi, ja kutsumme johtava kerroin. Polynomin aste on johtavan termin X: n potenssi. Olemme jo nähneet aste 0, 1 ja 2 polynomi, jotka olivat vakio, lineaarinen, ja quadratic toiminnot, vastaavasti. Asteen 3, 4 ja 5 polynomeilla on myös erityisiä nimiä: cubic, quartic, ja quintic funktiot. Polynomeja, joiden aste on n > 5, kutsutaan vain n: nnen asteen polynomeiksi. Eri polynomifunktioiden nimet on koottu alla olevaan taulukkoon.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
polynomien rajoittava käyttäytyminen
funktion rajoittava käyttäytyminen kuvaa, mitä funktiolle tapahtuu muodossa x → ±∞. Polynomin aste ja sen johtavan kertoimen merkki sanelee sen rajoittavan käyttäytymisen. Erityisesti
näistä tuloksista on yhteenveto alla olevassa taulukossa.
näiden tietojen avulla voidaan selvittää, onko polynomilla pariton vai parillinen aste ja onko johtava kerroin positiivinen vai negatiivinen, yksinkertaisesti tarkastamalla sen graafi.
seuraavat polynomien kuvaajat kuvaavat kutakin yllä olevassa taulukossa esitettyä käyttäytymistä.
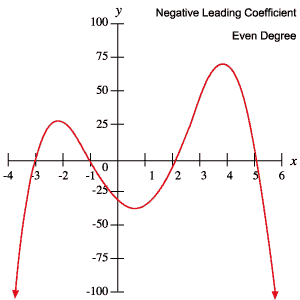
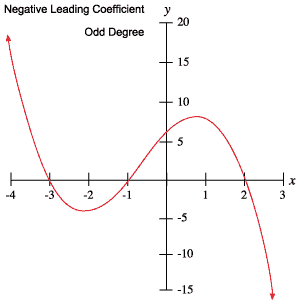
juuret ja käännekohdat
polynomin aste kertoo siitä vielä enemmän kuin rajoittava käyttäytyminen. Tarkemmin sanottuna n: nnen asteen polynomilla voi olla korkeintaan n reaalijuuret (x-interceptit tai nollat) laskien kertolaskuja. Oletetaan esimerkiksi, että tarkastelemme 6. asteen polynomi, joka on 4 erillistä juuret. Jos kaksi neljästä juuret on moninaisuus 2 ja muut 2 on moninaisuus 1, tiedämme, että ei ole muita juuria, koska olemme laskeneet kaikki 6 juuret. Tämä johtuu siitä, että juuret, joiden moninaisuus on kaksi (tunnetaan myös nimellä kaksoisjuuri) lasketaan kahdeksi juureksi.
huomaa, että n: nnen asteen polynomilla ei tarvitse olla n reaalisia juuria — sillä voisi olla vähemmän, koska sillä on kuvitteellisia juuria. Huomaa, että pariton asteen polynomi on oltava vähintään yksi todellinen juuri, koska funktio lähestyy – ∞ toisessa päässä ja + ∞ toisessa; jatkuva funktio, joka siirtyy negatiivisesta positiiviseen, leikkaa x – akselin jossain välissä. Lisäksi n: nnen asteen polynomilla voi olla korkeintaan n-1-kääntöpisteitä. Käännekohta on piste, jossa funktio muuttuu kasvavasta pienenevään tai vähenevästä suurenevaan, kuten alla olevassa kuvassa nähdään. Jälleen n: nnen asteen polynomilla ei tarvitse olla N-1-käännekohtia, sillä voisi olla vähemmän.
huomioitavaa
on tärkeää ymmärtää parillisten ja parittomien funktioiden sekä parillisten ja parittomien astepolynomien ero. Mikä tahansa funktio, f (x), on joko parillinen,
f(−x) = x,
kaikille x: lle F(x): n alueella, tai pariton, jos
f(−x) = −x,
kaikille x: lle f(x): n alueella, tai ei parillinen eikä pariton, jos kumpikaan edellä mainituista ei ole tosi lausuma.
k: n asteen polynomilla, p(x), sanotaan olevan parillinen aste, jos k on parillinen luku ja pariton aste, jos k on pariton luku. Muista, että vaikka p(x) on parillinen aste, se ei välttämättä ole parillinen funktio. Samoin, jos p (x) on pariton aste, se ei ole välttämättä pariton funktio.
käytämme myös termejä parillinen ja pariton kuvaamaan polynomien juuria. Erityisesti polynomilla p (x) on juuri x = A kerrannaisuudella k (eli x = A on juuri toistettuna k kertaa), jos (x − a) k on tekijä p(x). Sanomme, että x = a on parillinen kerrannaisuus, jos k on parillinen luku ja pariton kerrannaisuus, jos k on pariton luku.
domeeni ja alue
kaikilla polynomeilla on sama domeeni, joka koostuu kaikista reaaliluvuista. Parittomien astepolynomien joukko koostuu myös kaikista reaaliluvuista. Parillisten astepolynomien kantama on hieman monimutkaisempi,emmekä voi yksiselitteisesti ilmoittaa kaikkien parillisten astepolynomien kantamaa. Jos Johtava kerroin on positiivinen, funktio ulottuu arvoon+∞, kun taas jos Johtava kerroin on negatiivinen, se ulottuu arvoon – ∞. Tämä tarkoittaa sitä, että jopa asteen polynomi, jolla on positiivinen johtava kerroin, on alue, jossa ymax tarkoittaa kokonaismaksimia, jotka funktio saavuttaa. Polynomien maksimeja tai minimejä ei yleensä voida analyyttisesti määrittää.
****
seuraavassa osiossa opetellaan polynomijakoa, tekniikkaa, jolla etsitään polynomifunktioiden juuret.
Polynomijako