Expertise: Intermediate
What is a spline function?
meidän täytyy tietää, mitkä ovat linjojen olennaiset ominaisuudet, ennen kuin mietimme, miten rakentaa niille perusjärjestelmä.
Splinefunktiot muodostetaan liittämällä polynomit yhteen kiinteissä pisteissä, joita kutsutaan solmuiksi. Eli me jaamme intervalli ulottuu alaraja tL topper raja tu jonka yli haluamme likimäärin käyrä osaksi L + 1 sub-intervalsseparated jonka l sisäosien rajoja πl kutsutaan solmua, tai joskus breakpoints.)Näiden kahden termin välillä on ero, mutta palaamme tähän myöhemmin.
tarkastellaan yksinkertaisinta tapausta, jossa yksittäinen katkeamispiste jakaa intervallin kahdeksi alivoimaksi. Splinefunktio on kunkin intervallin sisällä tietyn asteen polynomi (polynomin määrittelevä korkein potenssi) tai kertaluku (polynomin määrittelevien kertoimien lukumäärä, joka on yksi enemmän kuin sen aste). Merkitään m: n avulla polynomin järjestys,jolloin aste on m – 1:
sisäisessä breakpoint π1: ssä kahden polynomin on liityttävä sujuvasti yhteen. Yleisimmässä tapauksessa tämä tarkoittaa, että derivaatat vastaavat järjestykseen yhtä astetta vähemmän. Itse asiassa, jos ne vastaavat jopa derivaatta, jonka kertaluku vastaa astetta, ne olisivat sama polynomi. Näin, spline funktio määritelty tässä oli on yksi ylimääräinen vapausaste kuin polynomi ulottuu koko intervalli.
esimerkiksi olkoon jokainen polynomi suora Jana ja siten aste yksi. Tässä ne liittyvät breakpoint kanssa vastaavat derivaatatup aste 0; lyhyesti sanottuna ne yksinkertaisesti liittyä ja joilla on samat arvot katkeamispisteessä. Koska ensimmäisellä polynomilla on kaksi vapausastetta (kaltevuus ja leikkauspiste), ja toisella, jonka arvo on jo määritelty katkeamispisteessä,on jäljellä vain yksi vapausaste (kaltevuus), on monikulmioisella viivalla kolme vapausastetta.
vastaavasti, jos molemmat polynomit ovat kvadratiikkaa, niin vastaavat sekä arvojen että ensimmäisen derivaatan δ1 slopen suhteen. Ensimmäisellä polynomilla on kolme vapausastetta, mutta toinen menettää kaksi, koska if-rajoitus sen arvolle ja kaltevuudelle on πi, ja siten säilyttää vain yhden. Tämä jättää yhteensä neljä astetta vapautta, splinefunctionformed tällä tavalla, asopposed kolme, joka quadratic polynomi koko intervalli. Kuva 1 osoittaa theselinear ja quadratic tapauksissa, joissa on yksi keskeytyspiste.
mitkä ovat joitakin esimerkkejä yleisesti käytetyistä perusfunktioista?
Voimme nyt yleistää tilanteen l interior breakpoints, anda spline funktio on järjestyksessä m tai aste m-1 Yli kunkin sub-intervalli. Ensimmäisellä polynomisegmentillä on täysi komplementaatio m: n vapausasteista, mutta jokaisella myöhemmällä janalla on vain yksi offreedom, koska m – 1 rajoittaa sen käyttäytymistä.Tämä antaa yhteensä L + m vapausasteet, tai määrä ofinterior breakpoints plus järjestyksessä polynomin segmenttien.
näin ollen splinefunktiot ovat oleellisesti monikulmiofunktioiden käsitteen yleistyksiä. Ne saavat joustavuutensa kahdella tavalla: ensinnäkin niiden polynomien järjestyksen mukaan, joista ne on rakennettu, ja toiseksi käytettyjen breakpointien määrän mukaan. Yleensä valitsemme pitää tilauksen kiinteänä, ja lisäämme keskeytyspisteitä tarpeen mukaan, jotta saamme tarvittavan joustavuuden.
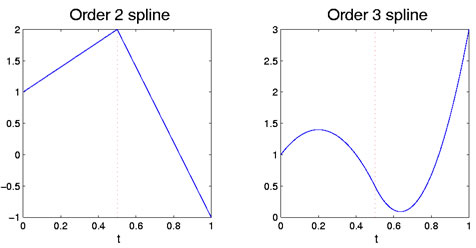
Kuva 1: vasemmassa kuvassa on järjestyksessä kaksi spline-funktiota, joka on paloittain lineaarinen. Oikea luku on järjestyksessä 3 spline, whichis piecewise quadratic. Breakpoint 0,5 on merkitty punaisella pystysuoralla katkoviivalla.