Fylogeneettisten verkkojen määritelmä
noudatamme Fylogeneettisten verkkojen määritelmää sellaisena kuin se on esitetty määritelmässä 4 , sivulla 16]. Kaikille muille graafiteoreettisille määritelmille, joita ei ole annettu tässä, seuraamme . Juurtunut fylogenetic verkko, yksinkertaisesti kutsutaan tässä fylogenetic verkko, on määritelty niin juurtunut, suunnattu asyklinen kuvaaja (DAG), jonka juuri on indegree 0 ja lehdet ovat outdegree 0. The vertices, joiden indegree on suurempi kuin 1 kutsutaan reticulate vertices ja reunojen kanssa reticulate vertices kuten pään vertices kutsutaan reticulate reunat. Kaikkia muita reunoja kutsutaan puiden reunoiksi. Määritelmä annetaan huolehtii niin sanottu” aika-johdonmukaisuus ”rajoitus, nimittäin, että puun reunat tapahtuvat positiivisessa ajassa ja reticulate vertices on vanhempia, jotka voivat vain”rinnakkain ajassa”. Siksi eteenpäin, muistamme muodollinen määritelmä fylogenetic verkkojen kuten esitetty .
koska mikä tahansa suunnattu kuvaaja, sanomme, että kaksi kärkipistettä u ja v eivät voi olla rinnakkain ajassa, jos on olemassa jono P = (p1, p2, …, p k) n: n poluista siten, että:
p i on suunnattu polku, joka sisältää vähintään yhden puunreunan, jokaista 1 ≤ i ≤ k,
u on P 1: n häntä ja v p k: n pää, ja
jokaista 1 ≤ i ≤ k – 1: n päätä kohden on verkkovinkki, jonka kaksi vanhempaa ovat Pää p i ja pyrstö p i+1.
fylogeneettinen verkko N on juurtunut DAG, joka noudattaa seuraavia rajoitteita:
-
jokainen huippupiste on indegree ja outdegree määritelty jollakin neljästä yhdistelmästä (0, 2), (1, 0), (1, 2), tai (2, 1) – vastaa vastaavasti juuri, lehdet, sisäinen puu vertices, ja reticulate vertices. Kaikki vertices muut kuin reticulate vertices kutsutaan tree vertices.
-
Jos kaksi kärkipistettä u ja v eivät voi olla rinnakkain ajan kanssa, ei ole olemassa verkon kärkipistettä w, jossa on reunat (u, w) ja (v, w).
-
kun otetaan huomioon mikä tahansa verkon reuna, ainakin yhden sen päätepisteistä on oltava puun kärkipiste.
toinen tämän määritelmän osatekijä on se, että fylogeneettisen verkoston mille tahansa reunalle ainakin yksi sen päätepisteistä (joko pää tai häntä) on puun kärkipiste. Tässä, käytämme tätä määritelmää. Korostamme mahdollisuuksien mukaan, ovatko määritelmän ehdot tarpeellisia.
fylogeneettisiä verkkoja voidaan naiivisti ajatella verkostona, joka sisältää alagrafeina ne puut, jotka selittävät syötepäätesarjojen eri segmenttien evoluutiohistoriaa. Koska fylogeneettinen verkko, poistamalla yksi kunkin reunan tapaus on reticulate huippupiste ei takaa tuloksena fylogenetic puu, jolla on sama joukko lehtiä kuin verkon. Tämä on ei-toivottu ominaisuus, varsinkin jos parsimonia kriteeri on määritelty löytämällä fylogeneettinen puu sisällä verkkoon, joka on kaikkein parsimonious tietyn sivuston, kuten määritelty . Tämän ongelman välttämiseksi on oletettava, että yhdelläkään sisäisellä vertexillä ei ole kahta reticulate-lasta. Kutsumme tätä fylogeneettisten verkostojen luokkaa fylogeneettiseksi verkostoksi, jolla ei ole sisarverkostoja. KS. Kuva 1 joitakin esimerkkejä fylogeneettisistä verkoista.
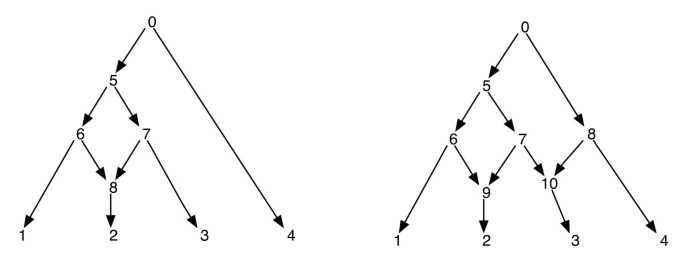
fylogeneettiset verkot. Kuvassa on kaksi fylogeneettistä verkkoa; vasemmalla on vain yksi reticulate huippupiste ja oikealla on kaksi reticulate vertices, jotka ovat sisters toisilleen. Huomaa, että reunojen (7, 9) ja (7, 10) poistaminen verkosta oikealla ei johda puuhun, jossa huippupiste 7 on lehti. Tämä osoittaa, että poistamalla yksi saapuva reuna kunkin reticulate huippupiste ei välttämättä tuottaa puu, jolla on sama lehtiä asetettu verkon. Verkon jälkitilaukset ja ennakkotilaukset vasemmalla ovat 1, 2, 8, 6, 3, 7, 5, 4, 0 ja 0, 5, 6, 1, 8, 2, 7, 3, 4 vastaavasti ja verkon oikealla, ne ovat 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 ja 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 vastaavasti.
ennen parsimiongelmien määrittelyä seuraava on hyödyllinen havainto. For a phylogenetic verkko N ilman sisar reticulations, ja ottaa R reticulate vertices ja lehtiä asetettu X, me kuvaamaan T ( N ) kuin joukko kaikki puut sisältyvät N. jokainen tällainen puu on saatu seuraavat kaksi vaihetta: (1) kunkin reticulate huippupiste, poista yksi saapuvien reunat, ja sitten (2) jokaisen huippupiste v, indegree ja outdegree 1, jonka vanhempi on u ja lapsi on w, sopimus reunat (u, v) ja (v, w) osaksi yhden reunan (u, w). Sillä edellytyksellä, että jokainen reuna N on puu huippupiste kuin päätepiste ja että jokainen puu huippupiste on vähintään yksi puu huippupiste kuin lapsi, varmistetaan, että joukko lehtiä tuloksena puu on sama kuin verkon. Näin ollen joukko T (N) sisältää täsmälleen 2rfylogeneettistä puuta, joiden lehtijoukko on täsmälleen X.
suurin Parsimonia
me viittaamme lukijoiden yleisen kuvauksen parsimonian ideasta ja erilaisten parsimonialgoritmien käsittelystä. On huomautettu, että puiden parsimismenetelmää voidaan laajentaa fylogeneettisiin verkkoihin. Sarjassa papereita, yksi tällainen parsimony kriteeri on määritelty löytää puu verkossa, joka on paras parsimonious pisteet, ja tehokkaita algoritmeja optimoida tämän kriteerin tietyn fylogeneettinen verkko on laadittu. Vaikka näiden algoritmien on osoitettu toimivan hyvin käytännössä, ne voivat toimia oikein vain fylogeneettisille verkoille, joilla ei ole sisarreaktioita, koska optimaalista puuta on helppo etsiä näistä rajatuista verkkoluokista. Tässä jaksossa, toteamme vaihtoehtoinen versio parsimony ongelma ja seuraavissa osissa tarjota joitakin heuristisia ratkaisuja optimoimalla pisteet tahansa fylogenetic verkkoon.
Let = {1, 2,…, n} merkitsee tietyn fylogeneettisen verkon N. A-funktion λ Leaf-nimikkeiden joukkoa: → {0, 1, …| / Σ / – 1} kutsutaan N: N aakkoston Σ (Ei-tyhjä joukko) tilakoodifunktioksi. sanomme, että funktio λ ^: V (N ) → { 0 , 1 , … , | Σ / – 1 } on λ: n laajennus N: llä, jos se yhtyy λ: n kanssa N: N lehdillä. For a huippupiste v in N, kutsumme λ ^ (v) kuin toimeksianto λ ^ on v. täysin osoitettu verkko on verkko, jossa kaikki vertices on tarroja {0, 1,…, |Σ| – 1}. Olkoon C kustannusmatriisi, jonka ijth merkintä C ij on kustannukset muuntaa tilasta i tilaan j pitkin mitään reunaa N. Jos e = (u, v) on reuna N, jossa u on vanhempi v, me merkitse w e ( λ) ^ = c i j , jossa i= λ ^ ( u) ja j= λ ^ ( v). For a kaavio G, annamme E (G) kuvaamaan reunan joukko G. sitten parsimony ongelma on määritelty seuraavasti.
Input: Fylogeneettinen verkko N, jossa on lehtimerkit ja tilaluokitusfunktio λ yli aakkosten Σ n: lle
Parsimoniakriteeri: laajennukselle λ ^ λ, olkoon
ja
Lähtö: annetaan P ∈ {P1, P2}, etsitään λ^, joka minimoi P ( λ ^ ) .
huomaamme, että P 1 ( λ ^ ) on otettu käyttöön ja P 2 ( λ ^ ) on määritelmä, jota käytämme tässä asiakirjassa. Yleisempi lähestymistapa on minimoida Q ( λ ^ ) = ∑ e ∈ E ( n ) d e ( W E ( λ ^ ) ) , jossa d e on ei-negatiivinen painofunktio n: n reunoilla.tässä asiakirjassa rajoitumme P = P2: een, vaikka ensimmäinen lähestymistapamme, dynaaminen ohjelmointiratkaisu pätee myös P = Q: lle.
Parsimonialgoritmit verkoissa
kulkevat fylogeneettisen verkon
verkossa, Vertex traversal viittaa prosessi vierailevat kunkin huippupiste, täsmälleen kerran, järjestelmällisesti. Tällaiset traversals luokitellaan järjestyksessä, jossa vertices ovat käyneet. Tarvitsemme kahdenlaisia verkon vertex traversals kuvaamaan algoritmeja. Nämä ovat tunnettuja fylogeneettisistä puista, ja me esittelemme niitä tässä fylogeneettisistä verkoista. Alla esitetyt algoritmit traversaleille alkavat mistä tahansa tietoverkon huippupiste v: stä. Tässä asiakirjassa, me aina suorittaa traversals alkaen root huippupiste verkon.
fylogeneettisen verkon ennakkotilaus verteksistä v
-
käy verteksissä v.
-
suorittaa rekursiivisesti ennakkotilausvuoroja jokaiselta lapselta, jolla ei ole vielä käyty.
fylogeneettisen verkon Post-order-traversio verteksistä v
-
suorittaa rekursiivisesti tilauksen jälkeisen traversion jokaiselta lapselta, jolla ei ole vielä käyty.
käy verteksissä v.
koska fylogeneettinen verkko on DAG, tällaiset kulkijat käyvät kaikissa verkon kärkipisteissä tasan kerran. (Katso lisätietoja olemassaolosta tällaisten traversals DAGs). Tätä varten tämän paperin, oletamme, että vertices, verkko ovat yksilöllisesti merkitty kokonaislukua. Huomaa, että lehdet on jo merkitty sarjasta ; ja niin käytämme muita kokonaislukuja muiden vertices. Aina kun lapsi vertices, v uutetaan, ne ovat myös järjestetty kasvavassa järjestyksessä niiden kokonaisluku labelings ja pre-ja post-order traversals suoritetaan tässä järjestyksessä. Näin varmistetaan seuraavat: jos vertices v ja v ’ovat sellaisia, että ei ole suunnattu polku niiden välillä, niin huippupiste v on kulkenut ennen huippupiste v’ in pre-order jos ja vain jos huippupiste v on kulkenut ennen huippupiste v’ in post-order. Katso joitakin esimerkkejä kuviosta 1. Tämän ominaisuuden avulla huomaamme, että ennen ja jälkeen tilauksen traversiot fylogeneettisen verkon juuresta jäljittävät kukin saman traversiopuun, jota kutsumme tässä traversiopuuksi.
dynaamista ohjelmointiratkaisua
dynaamista ohjelmointia käytetään tehokkaiden ratkaisujen tarjoamiseen tarkan parsimoniasteikon löytämiseen, kun verkko on fylogeneettinen puu . Tässä jaksossa osoitamme, että sama lähestymistapa voidaan yleistää fylogeneettisiin verkostoihin. Sankoff n algoritmi puu kulkee vertices, puu kautta post-order samalla computing vähimmäiskustannukset kunkin valtion kunkin huippupiste alkaen lehdet, root, ja sitten valitsee parhaat toimeksiannot kunkin huippupiste by backtracking alkaen juuri ja lehdet kulkemalla puun vertices kautta pre-order. Molemmat vaiheet on esitetty verkoille algoritmeissa 1 ja 2. Kuvailemme niitä lyhyesti alla. Voidaan todeta, että jos verkko on puu, niin algoritmimme vastaavat sankoffin menetelmän puiden ennakkotilaus-ja jälkitilausvaiheita.
kun otetaan huomioon fylogeneettinen verkko N, jonka lehtiverteet on merkitty ja jossa on tilan jakofunktio λ aakkosten Σ päällä, annetaan kullekin kärkipisteelle V ∈ V Suure s v (i) jokaiselle i ∈ Σ: lle. Vuonna fylogenetic puita, s v (i) merkitsee vähimmäissumma kustannusten kaikki tapahtumat alkaen huippupiste v kaikki lehdet, jotka ovat tavoitettavissa osoitteesta v, koska v on osoitettu valtion i ja kaikki descendant vertices osoitteesta v ovat kukin osoitettu valtion. Verkoissa ei ole yksinkertaista tapaa laskea tällaista määrää. Sen sijaan, Sallimme S v (i) on pienempi-raja edellä tarkka pisteet ja se lasketaan aikana post-order traversal vaiheessa.
Post-order traversal phase: jos v on n: n lehti, niin S v (i): lle annetaan 0, jos havaittu tila on tila i, ja ääretön muuten. Nyt kaikki mitä tarvitsemme on rekursio suhde laskea s v (i) muun vertices. Jokaisen lapsen w v, sanomme w täyttää post-order traversal ehto suhteen v, tai yksinkertaisesti traversal ehto suhteen v ottaen huomioon havainnon alussa tämän jakson, jos seuraavat hold:
- (i)
huippupiste w on retikuloitu huippupiste ja
- (ii)
Jos v’ on W: n muu kuin v: n emopiste, niin huippupiste v on läpäistävä ennen V: tä n: n post-order traversialissa
nyt määrittelemme rekursiivisesti jokaiselle reunalle (v, w),
for a fylogenetic tree, S(v, w)(I) always the first of these amounts, and it so gives the sum of the substitution costs pitkin the edge of the tree that lie below the vertex v, provided the vertex v is assigned the state i. For fylogenetic networks, in order for account for the substitution costs pitkin the edges that lie below a reticulate vertex w just a single time when vertex v is assigned the state i, we let the ”parent” v of w in the traversiopuun osuus kaikista korvaamiskustannuksista kaikilla V: n alapuolella olevilla reunoilla. On the other hand, if v is not an parent of w in the traversal tree, s (v, w) (i) simply merkitään korvaavan kustannukset valtion i klo huippupiste v toiseen tilaan W, joka on halvin.
tällöin määritellään
missä summa kulkee kaikkien lasten(ren) verteksien(s) w v. Kuten edellä mainittiin, fylogenetic puita, s v (i) merkitsee pienin mahdollinen summa korvaavien kustannusten pitkin kaikki reunat alkaen huippupiste v kaikki lehdet, jotka ovat tavoitettavissa osoitteesta v, koska v on osoitettu valtion i ja kaikki vertices tavoitettavissa osoitteesta v ovat kukin osoitettu valtion.
fylogeneettisissä verkoissa laskettaessa s(v, w)(i), jossa w on reticulate-kärkipiste siten, että (v, w) ei ole poikkipuun reuna, ei ole olemassa edeltävää tietoa tilasta, joka myöhemmin osoitetaan reticulate-kärkipisteessä w. Näin s(v, w)(i) voi olla vain alaraja reunojen verkon, jotka sijaitsevat alle huippupiste v, jos huippupiste v on osoitettu valtion I. perustelu tälle on, että s(v, w)(i) on korvaavan kustannukset valtion i klo huippupiste v toiseen tilaan W, joka on halvin, sen sijaan korvaavan kustannukset valtion i at V tilaan W, joka on myöhemmin osoitettu. Koska S v (i): n määritelmä riippuu s(v, w)(i): n määritelmästä, ja ne määritellään rekursiivisesti, noudatamme seuraavaa: S v (i) on alempi raja summa korvaavien kustannusten pitkin reunoja verkon, jotka ovat tavoitettavissa osoitteesta huippupiste v, edellyttäen, että v on osoitettu valtion i ja kaikki descendant tree vertices on osoitettu ainutlaatuinen tila, ja reticulate vertices on osoitettu kaksi valtiota, jotka eivät välttämättä ole sama. The assigned states, reticulate huippupiste edistää konfliktia, jos valtiot eivät ole samat. Oletetaan, että tila i on osoitettu juuri huippupiste r, ja kaikki puu vertices on osoitettu ainutlaatuinen tila, kun taas reticulate vertices on osoitettu kaksi valtiota. Sitten kustannukset s r (i) kristillisdemokraattien pienin mahdollinen summa korvaavien kustannusten pitkin kaikkia reunoja, traversal puu, jossa on yksi valtioiden osoitettu reticulate vertices, plus summa korvaavien kustannusten pitkin jäljellä reticulate reunat vaihtoehtoisen tehtävän tila on reticulate vertices. Koska pyrimme toimeksiannon, vertices, verkko, jolla ei ole ristiriitoja, reticulate vertices, s r (i) on alempi raja kustannukset tällaisen tehtävän, jossa juuri huippupiste on osoitettu i ja kaikki vertices on osoitettu ainutlaatuinen tehtävä.
tämän vaiheen aikana varastoidaan myös valtiot
jotta voidaan palauttaa w: n tila, joka saavuttaa suureen s(v, w)(i) pre-order-vaiheen aikana. Katso Algoritmi 1.
Pre-order traversial phase: valitsemme ensin minimin
, jossa r on juuriverteksi ja määritämme tilan, joka saavuttaa minimin juuriverteksissä, ts., olkoon λ ^ (r) = i r siten, että S r (i r) = S. kaikille muille huippupiste w, joka ei ole reticulate huippupiste, jonka vanhempi v on jo määritetty tilaan i, annamme tilan t(v, w) (i). Jotta reticulate huippupiste w jonka vanhemman vertices ovat v ja v”, olettakaamme, että v ja v ”on osoitettu todetaan i ja I” vastaavasti, kun traversing, jonka pre-order. W: n mahdollisten tilojen j = t(v, w)(i) ja j’ = t(v’, w)(i’), joilla saavutetaan s(v, w)(i) ja S(v’, w)(I’), ei tarvitse olla samat. Toisin sanoen on mahdollista, että J ≠ j’. Tällöin meillä on ristiriita reticulate huippupiste W. näin ollen dynaaminen ohjelmointitekniikka ei anna laajennusta λ, jonka parsimony pisteet on S. tässä tapauksessa me yksinkertaisesti valita J ja J ’λ (w) mukaan, mikä niistä vertices keskuudessa v ja v” on läpäisty ensin pre-order. Näin ollen, jos huippupiste w täyttää traversal ehto suhteen v meillä on λ ^ (w) =j.
suoritettuaan pre-order vaihe, voimme saada pisteet vastaavat laajennus λ ^ asettamalla ensin S ’= S ja päivittämällä S ’ kunkin reticulate vertex w seuraavasti: Yläraja s ’päivitetään vastaamaan jaottelua j vertex w: ssä s’ – c i ’ j ’+c i ’ J. Katso Algoritmi 2. Kuvassa 2 on esimerkki siitä, miten algoritmi toimii verkossa. Koska S r (i) on alempi raja on optimaalinen toimeksianto, jossa juuri huippupiste on osoitettu i ja kaikki vertices on osoitettu ainutlaatuinen toimeksianto, ja koska S = min i S r (i), voimme päätellä, että S on alempi raja, optimaalinen pyrimme löytämään. Katso aine 1 muodollinen todiste.

dynaaminen ohjelmointiratkaisu. Dynaamista ohjelmointiratkaisua sovelletaan fylogeneettiseen verkkoon. Osavaltiot ovat 0, 1 ja 2. Käytetty kustannusmatriisi on kaikki 1s paitsi diagonaalinen elementtejä, jotka ovat kaikki 0s. taulukot esitetty kunkin huippupiste v ovat kustannukset, s v (i) (toinen rivi) kunkin valtion, i (ensimmäinen rivi), jotka on laskettu aikana post-order traversal. Myös esitetty, vertices ovat valtioiden lapsen w, eli t(v, w) (i) (kolmas rivi), jotka vastaavat kustannuksia toisella rivillä, kun on olemassa kaksi lasta, jonka huippupiste, merkinnät kolmannella rivillä ovat edustettuina kuin pari valtioiden vasen lapsi ja oikea lapsi vastaavasti. Jokainen reuna (v, w) on merkitty S(v, w) (i) kunkin tilan i. aikana pre-order traversal, tilat kunkin huippupiste valitaan (lihavoitu). Kustannukset 2 korostettu lihavoitu on juuri huippupiste antaa alemman rajan, S. valtion määritetty kunkin huippupiste on korostettu lihavoitu. Algoritmi löytää yhteensä kolme sijamuotoa (korostettuna lihavoiduilla reunoilla). Tämä johtuu siitä, että valtioiden annetaan klo vanhemman vertices, reticulate huippupiste antaa ristiriitaisia toimeksiantoja 1 ja 2 vastaavasti, joista Valtion 1 on osoitettu klo reticulate huippupiste. Siten ylimääräinen kustannus 1, saamme pisteet 3 (yläraja optimaalinen pisteet) kuin parsimony pisteet vastaavat tehtävän esitetty. Huomaa, että optimaalinen parsimony pisteet verkossa on 2 (yhtä suuri kuin alempi raja), joka löytyy tyhjentävä haku ja voidaan toteuttaa muuttamalla tehtävän 1-2 vasemmalle vanhempi, reticulate huippupiste ja 1-2, reticulate huippupiste. Näin ollen alaraja vastaa optimaalista pistemäärää, vaikka alarajaa vastaava tehtävä ei ole ristiriidaton eikä sama kuin optimia vastaava tehtävä.
heidät 1. Suure S on verkon optimaalisen parsimoniapisteen alaraja N.
Proof. S : n konstruktiolla saadaan
missä toinen summand on retikulaattiverteksi w, jonka vanhemmat ovat v ja v ” siten, että v täyttää traverssal ehto w.r.t. w. siten kustannus C λ ^ ( v ) , λ ^ ( W ) on korvauskustannus määrätystä tilasta λ ^ ( V ) at V tilaan λ ^ ( W ) at W. Toisaalta kustannus C λ ^ (v’), t ( v’, w) (λ ^ ( v’)) on korvauskustannus määrätystä tilasta λ ^ ( v) pisteessä V tilaan t ( v’, w) (λ ^ ( v’)) pisteessä W. huomaa , että tila t ( v’, w) (λ ^ ( V’)) ei ole välttämättä sama kuin tila λ ^ ( w), ja S on pienin kaikista toimeksiannoista, jotka voivat aiheuttaa ristiriitoja reticulate-kärkipisteissä.
Oletetaan, että S ^ on optimaalinen parsimoniasteikko N: llä funktiolla μ: V (N) → {0, 1, …,| Σ / – 1} λ: n laajennuksena meillä on
, jossa toisessa summandissa w on retikuloitu kärkipiste, jonka vanhemmat ovat v ja v”. Koska μ on ristiriidaton toimeksianto, joka sisältyy kaikkien toimeksiantojen joukkoon, joiden kustannukset S on pienin (vertaa yhtälö (3) ja (4)), meillä on S≤ S ^ . □
nyt algoritmin monimutkaisuudesta. Oletetaan verkon N on n lehdet ja r reticulate vertices. Silloin n: n kärkipisteiden lukumäärä on 2(n + r) -1. Kussakin kärkipisteessä v ja kussakin tilassa i Suure S voidaan laskea O (k2) – ajassa, jossa k = |Σ|. The pre-order traversal vaihe liittyy löytää S O (k) monimutkaisuus ja määrittämällä parhaat valtiot kunkin huippupiste. Myös, vahvistamisesta ristiriitaisia reticulate huippupiste valtioiden vie O (r) aikaa. Siten monimutkaisuus algoritmin (esitetty tässä) löytää alempi ja ylempi raja on O ((n + r)k2). Vaihtoehtoinen yläraja voidaan saada O (nk2) yksinkertaisesti määrittämällä aikana post-order traversal vaiheessa, kunkin reticulate huippupiste tila, joka tapahtuu enimmäismäärä kertaa lehdet tavoitettavissa vastaavien reticulate huippupiste; ja jatkamalla kautta löytää S v (i) jäljellä vertices. Tarkka optimaalinen voidaan myös saada rajoittamalla mahdolliset valtiot yhteen tilaan kunkin reticulate huippupiste, ajamalla dynaaminen ohjelmointi algoritmi kunkin kr yhdistelmiä valtioiden reticulate vertices,ja valitsemalla vähintään joukossa kaikki. Tämän prosessin ajallinen monimutkaisuus on O (nkr+2).
algoritmi 1 Post-order traversal phase: lasketaan kunkin tilan kustannukset kussakin huippupisteessä
- 1:
Input: Verkko n ja havaitut tilat Σ: STA n: n lehdissä, eli tilaluokitusfunktio λ yli aakkosten Σ n: lle
- 2:
jokaiselle lehdelle v, olkoon S v (i) = 0 jos λ(v) = i ja ∞ muuten.
- 3:
toista jälkijärjestyksessä kullekin sisäisessä kärkipisteessä (juuri, sisäinen puu vertex tai reticulate vertex) V N: ssä: Kunkin tilan i osalta lasketaan 1 kohdassa annettu S v (i) ja 2 kohdassa annettu t (v, w) (i) jokaiselle V: n lapselle.
- 4:
Lähtö: {(S v (i),): v ∈ v (n), i ∈ Σ}.
minimoimalla mutaatioiden määrä fylogeneettisessä verkossa
Fitchin algoritmi laskee bifurkoivan fylogeneettisen puun muutosten määrän mille tahansa merkistölle, jossa tilat voivat muuttua mistä tahansa tilasta mihin tahansa toiseen tilaan. Näin kustannusmatriisi on sellainen, että sen diagonaalielementit ovat kaikki nollia ja off-diagonaaliset alkiot ovat kaikki ykkösiä. Tässä jaksossa näytämme, miten Fitchin algoritmi ulottuu ylä-ja alarajojen löytämiseen tietyn fylogeneettisen verkon evoluutiomuutosten määrälle. Ensinnäkin, osoitamme, että Fitch algoritmi voidaan laajentaa antaa yläraja optimaalinen parsimony pisteet. Kuten aiemminkin, jälkitilaus-ja ennakkotilausvaiheet on esitetty algoritmeissa 3 ja 4 alla. Katso kuva 3 esimerkki ajaa algoritmin.

Fitch-tyyppinen ratkaisu. Fitch – tyyppistä ratkaisua sovellettiin samaan fylogeneettiseen verkkoon ja kuvan 2 lehtitietoihin. Jokainen huippupiste on osoitettu joukko kaikkia mahdollisia valtioita, yhdessä pisteet, kun verkon vertices ovat kulkeneet post-order. Juuressa oleva pistemäärä antaa ylärajan optimaaliselle pistemäärälle. Valtion tehtävät annetaan pre-order-traversiovaiheessa ja sijaisten määrä vastaa juuressa olevaa pistemäärää.
algoritmi 2 ennakkomaksuvaihe: Lasketaan optimin ala-ja ylärajat sekä vastaava ylärajan jako
- 1:
Tulo: {(S v (i), ): v ∈ v (n), i ∈ Σ}.
- 2:
Let s = min i S r (i), missä r on juuriviiva ja let λ ^ ( r ) =arg min i S r ( i ) .
- 3:
Let S’ = S
- 4:
jokaiselle kärkipisteelle w esijärjestyksessä, jonka kantaverkosto v prekessoi välittömästi w: n , olkoon λ ^ ( ω ) = t v , w ( i), missä i= λ ^ ( v ) .
- 5:
käy jokaisessa reticulate vertex w: ssä vanhempien v ja v’ kanssa siten, että w täyttää läpivirtausehdon V: n suhteen , I= λ ^ ( v), i ’= λ ^ ( v’), j ’= t ( v’, w ) ( i ) ja päivittää S’ seuraavasti:
S ’← S ’- C i ’ j ’+ c i ’ J . - 6:
Output: (Lower bound, Upper bound) = (S, S’); extension againing to the upper bound score S”: λ ^ .
algoritmi 3 post-order traversal phase: Calculate the optimum
- 1:
Input: Fylogeneettinen verkko N ja tilaluokitusfunktio λ yli aakkosten Σ n: lle
- 2:
jokaiselle n: n lehdelle v annetaan A(v) = {λ(v)}, singleton joukko, joka sisältää havaitun tilan lehden kohdalla.
- 3:
Set UB = 0.
- 4:
rekursio käyttäen jälkijärjestystä: T: n verteksille v, jolla on lapsia w1 ja w2, olkoon ja jos verteksillä v on yksi lapsi w, niin
ja
5: ({a(v): v ∈ V (N)}, UB)
koska pre-order traversal-vaihe antaa ristiriitaisen jaon kärkipisteille, UB on yläraja. Tämä on erikoistapaus yleiselle kustannusmatriisille esitetystä dynaamisesta algoritmista. Oletetaan, että rajoitamme N: N fylogeneettiseksi verkoksi, jolla ei ole sisarreaktioita, niin mikä tahansa Fitch-ratkaisu missä tahansa puussa T (n) muodostaa alarajan verkkojen optimaaliselle pisteytykselle; ja lisäämällä kustannukset reunat ei t antaa yläraja optimaalinen pisteet. Näin ollen on mahdollista laskea meidän alaraja merkkimuutosten määrän laskemiseksi vain fylogeneettisille verkoille, joilla ei ole sisarreaktioita, jolloin on suoraviivaista löytää Puu T ( N): ssä .
algoritmi 4 Pre-order traversal phase: Assigning the states
- 1:
Input: Fylogenetic tree N and ({a(v): v ∈ V (N)}, UB).
- 2:
jokaiselle sellaisen puun kärkipisteelle v, jota ei ole vielä määritetty, algoritmi laskee λ ^ (v) seuraavasti: Juuren R osalta λ ^ (r) =σ, missä σ on mielivaltainen alkio a(r). Määritä rekursiivisesti ennakkojärjestyksen kautta: verteksille v, jonka emoarvo u on annettu,
λ ^ ( v ) = λ ^ ( u), jos λ ^ ( u ) ∈ A ( v ) ; σ ∈ A ( v ) muutoin . - 3:
pisteytyksen vahvistaminen: jokaiselle retikuloidulle kärkipisteelle v, Jos u’ ei ole lähtöjärjestyksessä, ja jos λ ^ ( u ’) ∈a ( v ) , mutta λ ^ ( u ’ ) ≠ λ ^ ( v ) , lisätään UB 1: llä.
- 4:
Lähtö: UB – ja laajennusfunktio λ ^ λ.