Luokitustekniikat ovat olennainen osa koneoppimista ja tiedonlouhintasovelluksia. Noin 70 prosenttia datatieteen ongelmista on luokitteluongelmia. On olemassa paljon luokitteluongelmia, jotka ovat käytettävissä, mutta logistiikan regressio on yleinen ja on hyödyllinen regressiomenetelmä binäärisen luokitteluongelman ratkaisemiseksi. Toinen luokitteluluokka on Multinomial classification, joka käsittelee asioita, joissa kohdemuuttujassa on useita luokkia. Esimerkiksi IRIS dataset erittäin kuuluisa esimerkki multi-luokan luokittelu. Muita esimerkkejä ovat luokittelu artikkeli / blogi / asiakirjaluokka.
logistista regressiota voidaan käyttää erilaisiin luokitteluongelmiin, kuten roskapostin tunnistamiseen. Diabeteksen ennustaminen, jos tietty asiakas ostaa tietyn tuotteen tai he kirnuavat toinen kilpailija, onko käyttäjä klikkaa tietyn mainoksen linkkiä tai ei, ja monia muita esimerkkejä ovat ämpäri.
logistinen regressio on yksi yksinkertaisimmista ja yleisimmin käytetyistä Koneoppimisalgoritmeista kahden luokan luokittelussa. Se on helppo toteuttaa ja sitä voidaan käyttää minkä tahansa binääriluokitusongelman pohjana. Sen peruskäsitteet ovat rakentavia myös syväoppimisessa. Logistinen regressio kuvaa ja arvioi yhden riippuvaisen binäärimuuttujan ja riippumattomien muuttujien suhdetta.
tässä opetusohjelmassa opit seuraavat asiat logistisessa regressiossa:
- Johdatus logistiseen regressioon
- lineaarinen regressio Vs. logistinen regressio
- suurin Todennäköisyysarvio Vs. tavallinen pienimmän neliösumman menetelmä
- miten logistinen regressio toimii?
- Model building in Scikit-learn
- Model Evaluation using Confusion Matrix.
- logistisen Regression edut ja haitat
logistinen regressio
logistinen regressio on tilastollinen menetelmä binääriluokkien ennustamiseksi. Tulos-tai kohdemuuttuja on luonteeltaan dikotominen. Dikotomia tarkoittaa, että mahdollisia luokkia on vain kaksi. Sitä voidaan käyttää esimerkiksi syövän havaitsemisongelmiin. Se laskee tapahtuman todennäköisyyden.
se on lineaarisen regression erikoistapaus, jossa kohdemuuttuja on luonteeltaan kategorinen. Se käyttää log kertoimet kuin riippuvainen muuttuja. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
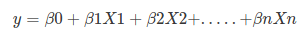
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
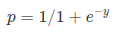
Apply Sigmoid function on linear regression:
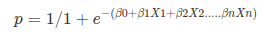
Properties of Logistic Regression:
- logistisessa regressiossa riippuvainen muuttuja noudattaa Bernoullin jakaumaa.
- estimointi tehdään suurimman todennäköisyyden kautta.
- No R Square, Model fitness lasketaan konkordanssin, KS-tilastojen kautta.
lineaarinen regressio Vs. logistinen regressio
lineaarinen regressio antaa jatkuvan ulostulon, mutta logistinen regressio antaa jatkuvan ulostulon. Esimerkki jatkuvasta tuotoksesta on asuntojen hinta ja osakekurssi. Esimerkki: n diskreetti tuotos ennustaa, onko potilaalla on syöpä vai ei, ennustaa, onko asiakas Kirnu. Lineaarinen regressio arvioidaan tavallisen pienimmän neliösumman (OLS) avulla, kun taas logistinen regressio arvioidaan suurimman todennäköisyyden estimoinnin (MLE) avulla.
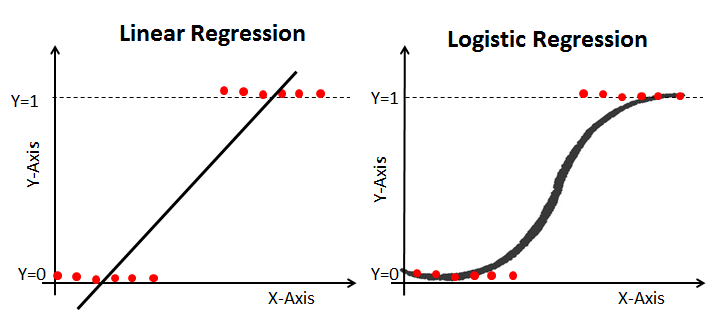
suurimman todennäköisyyden estimointi Vs. pienimmän neliön menetelmä
MLE on ”todennäköisyyden” maksimointimenetelmä, kun taas OLS on etäisyyden minimoiva likiarvomenetelmä. Todennäköisyysfunktion maksimointi määrittää parametrit, jotka todennäköisimmin tuottavat havaitun datan. Tilastollisesta näkökulmasta MLE asettaa keskiarvon ja varianssin parametreiksi määritellessään tietyn mallin ominaisparametriarvoja. Tätä muuttujien joukkoa voidaan käyttää normaalijakaumassa tarvittavan tiedon ennustamiseen.
tavalliset pienimmän neliösumman estimaatit lasketaan asentamalla annettuihin datapisteisiin regressiolinja, jolla on neliöpoikkeamien vähimmäissumma (pienimmän neliösumman virhe). Molempia käytetään lineaarisen regressiomallin parametrien estimointiin. MLE olettaa yhteisen todennäköisyysmassafunktion, kun taas OLS ei vaadi stokastisia oletuksia etäisyyden minimoimiseksi.
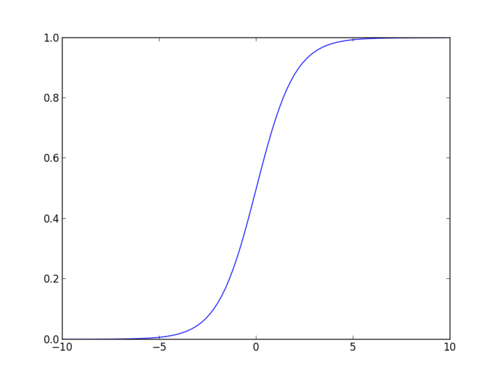
Sigmoidifunktio
sigmoidifunktio, jota kutsutaan myös logistiseksi funktioksi, antaa ”S”: n muotoisen käyrän, joka voi ottaa minkä tahansa reaaliarvoisen luvun ja kartoittaa sen arvoksi välillä 0 ja 1. Jos käyrä menee positiiviseen äärettömyyteen, ennustetusta y: stä tulee 1, ja jos käyrä menee negatiiviseen äärettömyyteen, ennustetusta y: stä tulee 0. Jos sigmoidifunktion ulostulo on yli 0,5, voimme luokitella tuloksen 1 tai kyllä, ja jos se on alle 0.5, voimme luokitella sen 0 tai ei. Ulostulo ei voi olla esimerkki: Jos lähtö on 0,75, voimme sanoa kannalta todennäköisyys: on 75 prosentin mahdollisuus, että potilas kärsii syövästä.
logistisen regression tyypit
logistisen regression tyypit:
- binäärisen logistisen regression: kohdemuuttujalla on vain kaksi mahdollista lopputulosta, kuten roskaposti tai ei roskapostia, syöpä tai ei syöpää.
- monikansallinen logistinen regressio: kohdemuuttujalla on kolme tai useampia nimellisiä luokkia, kuten viinityypin ennustaminen.
- Ordinaalinen logistinen regressio: kohdemuuttujalla on kolme tai useampia ordinaaliluokkia, kuten ravintola-tai tuoteluokitus 1-5.
Mallirakennus Skikit-opissa
rakennetaan diabeteksen ennustemalli.
tässä ennustat diabetesta logistisen Regressioluokituksen avulla.
ladataan ensin tarvittava Pima Indian Diabetes-tietokokonaisuus pandojen luetun CSV-toiminnon avulla. Voit ladata tiedot seuraavasta linkistä: https://www.kaggle.com/uciml/pima-indians-diabetes-database
Lastaustiedot
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
valitsemalla ominaisuuden
tässä on jaettava annetut sarakkeet kahteen muuttujatyyppiin riippuvaisiksi(tai kohdemuuttujiksi) ja itsenäisiksi muuttujiksi(tai ominaisuusmuuttujiksi).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variabletietojen jakaminen
mallin suorituskyvyn ymmärtämiseksi tietokokonaisuuden jakaminen koulutus-ja koesarjaan on hyvä strategia.
jaetaan tietojoukko funktion train_test_split () avulla. Sinun täytyy siirtää 3 parametrit ominaisuuksia, tavoite, ja test_set koko. Lisäksi, voit käyttää random_state valita tietueita satunnaisesti.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)tässä aineisto on jaettu kahteen osaan suhteessa 75:25. Se tarkoittaa, että 75 prosenttia tiedoista käytetään mallikoulutukseen ja 25 prosenttia mallikokeiluun.
Model Development and Prediction
tuo ensin logistinen Regressiomoduuli ja luo logistinen Regressioluokituskohde käyttäen LogisticRegression () – funktiota.
tämän jälkeen sovita mallisi junajoukkoon käyttäen fit () – menetelmää ja suorita testijoukolle ennustus käyttäen predict () – menetelmää.
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)mallin arviointi käyttäen Sekaannusmatriisia
sekaannusmatriisi on taulukko, jota käytetään luokitusmallin suorituskyvyn arviointiin. Voit myös visualisoida algoritmin suorituskyvyn. Sekaannusmatriisin perusolemuksena on oikeiden ja virheelliset ennustukset summataan luokkakohtaisesti.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])Tässä näkyy sekaannusmatriisi array-objektin muodossa. Tämän matriisin dimensio on 2*2, koska tämä malli on binääriluokitus. Teillä on kaksi luokkaa 0 ja 1. Diagonaaliset arvot edustavat tarkkoja ennusteita, kun taas ei-diagonaaliset elementit ovat epätarkkoja ennusteita. Tuotoksessa 119 ja 36 ovat todellisia ennusteita ja 26 ja 11 virheellisiä ennusteita.
visualisoidaan Sekaannusmatriisia käyttäen heatmap
visualisoidaan mallin tulokset sekaannusmatriisin muodossa matplotlibin ja seabornin avulla.
tässä näet sekaannusmatriisin heatmapin avulla.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
sekaannusmatriisin arviointimittarit
arvioidaan mallia käyttäen mallin arviointimittareita, kuten tarkkuutta, tarkkuutta ja takaisinkutsua.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226no, sait 80%: n luokitusasteen, jota pidetään hyvänä tarkkuutena.
tarkkuus: tarkkuudessa on kyse tarkkuudesta eli siitä, kuinka tarkka malli on. Toisin sanoen, kun malli tekee ennusteen, voi sanoa, kuinka usein se on oikein. Ennustamistapauksessanne, kun logistinen Regressiomallinne ennusti potilaiden kärsivän diabeteksesta, että potilailla on 76% ajasta.
muista: jos testisarjassa on potilaita, joilla on diabetes ja logistinen Regressiomallisi tunnistaa sen 58% ajasta.
ROC-käyrä
vastaanottimen Toimintaominaisuuskäyrä(Roc) on kuvaaja, joka kuvaa todellista positiivista korkoa suhteessa väärään positiiviseen korkoon. Se osoittaa herkkyyden ja spesifisyyden välisen kaupan.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
AUC-pisteet tapaukselle ovat 0, 86. AUC-pisteet 1 edustavat täydellistä luokittelijaa ja 0,5 arvotonta luokittelijaa.
edut
koska se on tehokas ja suoraviivainen, se ei vaadi suurta laskentatehoa, helppo toteuttaa, helposti tulkittavissa, jota data-analyytikko ja tiedemies käyttävät laajalti. Myös, se ei vaadi skaalaus ominaisuuksia. Logistinen regressio antaa havainnoille todennäköisyyspisteen.
haitat
logistinen regressio ei pysty käsittelemään suurta määrää kategorisia piirteitä / muuttujia. Se on altis liikakalastukselle. Ei myöskään voi ratkaista epälineaarista ongelmaa logistisella regressiolla, minkä vuoksi se vaatii epälineaaristen ominaisuuksien muuntamista. Logistinen regressio ei menesty hyvin riippumattomilla muuttujilla, jotka eivät korreloi kohdemuuttujan kanssa ja ovat hyvin samankaltaisia tai korreloituneita keskenään.
johtopäätös
tässä opetusohjelmassa käsittelit paljon yksityiskohtia logistisesta regressiosta. Olet oppinut, mitä logistinen regressio on, miten rakentaa vastaavia malleja, miten visualisoida tuloksia ja joitakin teoreettisia taustatietoja. Käsittelit myös joitakin peruskäsitteitä, kuten sigmoid-funktio, suurin todennäköisyys, sekaannusmatriisi, ROC-käyrä.
toivottavasti voit nyt hyödyntää logistista Regressiotekniikkaa analysoidaksesi omia tietokokonaisuuksiasi. Kiitos tämän opetusohjelman lukemisesta!
Jos haluat oppia lisää logistisesta regressiosta, ota Datacampin Foundations of Predictive Analytics in Python (Osa 1) – kurssi.