tarkastellaan elektronitiheyden delokalisoitumista. Tällöin elektronitiheys leviää mahdollisimman paljon molekyylin koko alueelle, jolloin vähimmäisvarauksen kertyminen on läsnä tietyllä orbitaalilla.
, joka on kuvattu:
- kollektiivisesti kaikki Lewisin rakenteiden resonanssivaikuttajat.
- kollektiivisesti kaikkien yksittäisten molekyyliorbitaalien osuudet molekyyliorbitaalikaavioissa.
(näiden välillä on hiuksenhienoja eroja, mutta nämä ovat yksinkertaisuudessaan suunnilleen analogisia. Katso tästä tarkemmin.)
Elektronitiheyden lokalisointi on sen puute.
kyse on siitä, kun tunkemme kaiken elektronitiheyden muutamille orbitaaleille sen levittämisen sijaan, eikä sitä juuri koskaan tapahdu todellisessa molekyylissä tai kvanttijärjestelmässä (vaikka resonanssia ei olisikaan).
esimerkki RESONANSSIRAKENTEISTA
pitävät eristettyä (reagoimatonta) allyylikationia, #”C”_3″H”_5^(+)#.
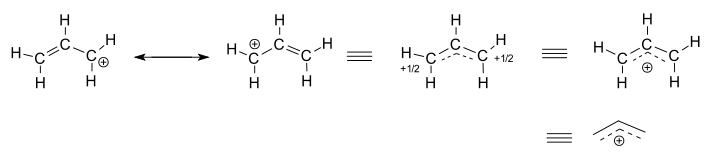
- vasemmanpuoleiset kaksi rakennetta ovat resonanssivaikuttajia, joista kumpikin on lokalisoitu representaatio todellisesta delokalisoituneesta rakenteesta.
- kolme oikeanpuoleista rakennetta ovat kukin resonanssihybridirakenteen eli delokalisoituneen rakenteen representaatioita.
delokalisoitunutta rakennetta kuvaa pohjimmiltaan kokoelma sidosmolekyyliorbitaaleja.
esimerkki MOLEKYYLIORBITAALIKAAVIOLLA
tarkastellaan allyylikationia uudelleen MO-diagrammissa, joka kuvaa vain #bbpi# – elektroneja (eli elektroneja, jotka olisivat #pi# – sidoksessa lokalisoidussa kaksoissidoksessa!), mutta sallii osallistumisen reaktioihin:
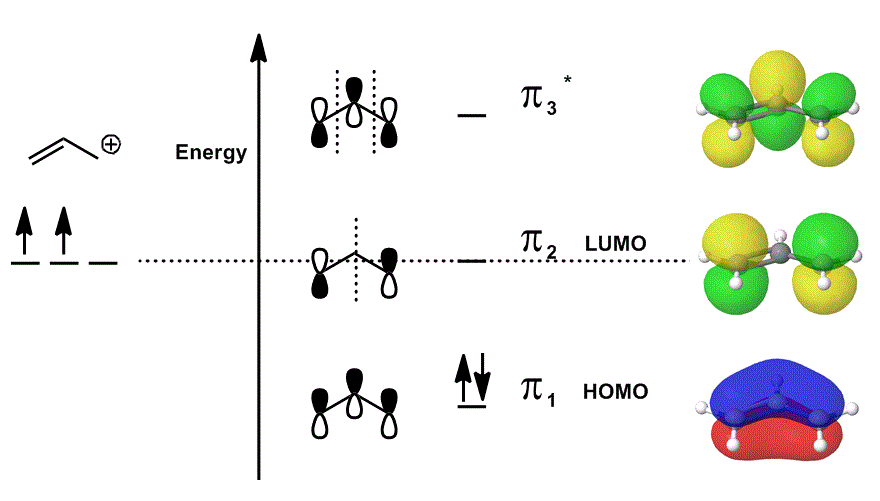
- jokainen keskellä oleva orbitaali on kuvattu lokalisoituna; päällekkäiset atomiorbitaalit esitetään omana itsenään (vaihe mukaan lukien).
- jokainen äärioikeiston orbitaaleista (yksi per rivi) on kuvattu delokalisoituneena; elektronitiheyden annetaan levittäytyä niin, että molekyyliorbitaalit kuvataan ottaen täysin huomioon päällekkäisyydet, solmut ja faasit.
kun limitetään #pi_1#, #pi_2# ja #pi_3^”*”# ja sisällytetään näiden tilojen painotettu osuus (painotettuna kertoimilla #c_i#), saadaan molekyyliorbitaalien lineaarinen yhdistelmä:
#psi_(”allyl”^(+)) = c_1overbrace(pi_1)^”bonding” + c_2overbrace(pi_2)^”nonbonding” + c_3overbrace(pi_3^”*”)^”antibonding”#
ja #Psi_(”allyl”^(+))# then kuvaa allyylikationin reaktiivisuutta kollektiivisesti kuvaavien tilojen kokonaisjakaumaa.
toisin sanoen #pi_1# (joka lahjoittaa #pi# elektronit sidokseen), #pi_2# (joka hyväksyy elektronit sidokseen) ja #pi_3^”*”# (tässä tapauksessa se harvoin osallistuu) tekevät kaikki jotain allyylikationin osallistuessa kemialliseen reaktioon, koska (jos käytössä) ne ovat olemassa samanaikaisesti.