Normaalijakaumat (kellokäyrä): määritelmä, Sanaongelmat

todennäköisyys ja tilastot >Normaalijakaumat

sisältö:

1. mikä on Normaalijakauma?
2. normaali malli
3. normaalijakauman Sanaongelmat.
4. Normaalijakauma TI 89 esimerkistä
5. aiheeseen liittyvistä artikkeleista.

mikä on Normaalijakauma?

Normaalijakauma.

normaalijakauma, jota joskus kutsutaan kellokäyräksi, on monissa tilanteissa luonnostaan esiintyvä jakauma. Kellokäyrä näkyy esimerkiksi SAT: n ja GRE: n kaltaisissa testeissä. Suurin osa opiskelijoista pisteet keskimäärin (C), kun taas pienempi määrä opiskelijoita pisteet B tai D. vielä pienempi osa opiskelijoista pisteet F tai A. Tämä luo jakauma, joka muistuttaa bell (siksi lempinimi). Kellokäyrä on symmetrinen. Puolet tiedoista putoaa keskiarvon vasemmalle puolelle, puolet oikealle.
monet ryhmät noudattavat tällaista kaavaa. Siksi sitä käytetään laajasti liike-elämässä, tilastoissa ja valtion elimissä, kuten FDA:

• ihmisten korkeudet.
• mittausvirheet.
• verenpaine.
• pisteet kokeesta.
• ÄO-pisteet.
• palkat.

empiirinen sääntö kertoo, kuinka suuri prosenttiosuus datasta sijoittuu tietyn keskihajonnan sisään keskiarvosta:
• 68% datasta sijoittuu yhden keskihajonnan sisään keskiarvosta.
• 95% tiedoista on keskiarvon kahden keskihajonnan sisällä.
• 99,7% tiedoista on keskiarvon kolmen keskihajonnan sisällä.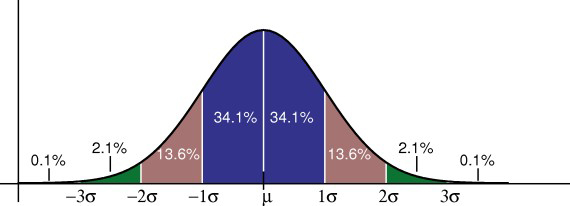

keskihajonta ohjaa jakauman leviämistä. Pienempi keskihajonta osoittaa, että tiedot ryhmittyvät tiiviisti keskiarvon ympärille; normaalijakauma on pitempi. Suurempi keskihajonta osoittaa, että aineisto jakautuu keskiarvon ympärille; normaalijakauma on tasaisempi ja laajempi.

normaalijakauman ominaisuudet

• keskiarvo, moodi ja mediaani ovat kaikki yhtä suuret.
• käyrä on symmetrinen keskipisteessä (eli keskiarvon ympärillä, μ).
• tasan puolet arvoista on keskellä vasemmalla ja tasan puolet arvoista oikealla.
• käyrän alittava kokonaispinta-ala on 1.

normaali Normaalimalli
normaali normaalimalli on normaalijakauma, jonka keskiarvo on 0 ja keskihajonta 1.

normaali Normaalimalli: Tietojen jakautuminen

yksi tapa selvittää, miten tiedot jakautuvat, on piirtää ne kuvaajaksi. Jos tiedot ovat tasaisesti jakautuneet, voit keksiä kellokäyrän. Kellokäyrällä on pieni prosentti molempien häntien pisteistä ja suurempi prosentti käyrän sisäosan pisteistä. Normaalissa normaalimallissa noin 5 prosenttia tiedoistasi putoaisi ”hännille” (värillinen tummempi oranssi alla olevassa kuvassa) ja 90 prosenttia on niiden välissä. Esimerkiksi opiskelijoiden koepisteissä normaalijakauma näyttäisi 2,5 prosenttia opiskelijoista saavan hyvin alhaiset pisteet ja 2.5 prosenttia saa erittäin korkeat pisteet. Loput ovat keskellä; ei liian korkealla eikä liian matalalla. Normaalijakauman muoto näyttää tältä:

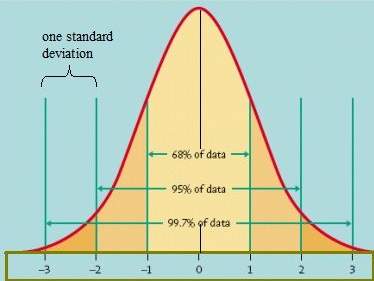
normaali normaalimalli. Image credit: University of Virginia.

Standardinormaalimallin käytännön sovellutukset

standardinormaalijakauma voisi auttaa selvittämään, mistä oppiaineesta saat hyviä arvosanoja ja mihin koehenkilöihin sinun on panostettava enemmän alhaisten pisteytysprosenttien vuoksi. Kun saat pisteet yhdestä aiheesta, joka on korkeampi kuin pisteet toisessa oppiaineessa, saatat ajatella, että olet parempi aihe, jossa sait korkeammat pisteet. Tämä ei ole aina totta.

voit sanoa, että olet parempi tietyssä oppiaineessa vain, jos saat pistemäärän, jossa on tietty määrä keskiarvon ylittäviä keskihajontoja. Keskihajonta kertoo, kuinka tiukasti tiedot on ryhmitelty keskiarvon ympärille; sen avulla voit vertailla eri jakaumia, joilla on erityyppisiä tietoja – myös eri keinoja.

esimerkiksi jos matematiikassa saa arvosanaksi 90 ja englannin kielessä 95, voi luulla olevansa parempi englannin kielessä kuin matematiikassa. Matematiikassa pistemääräsi on kuitenkin 2 keskihajontaa keskiarvon yläpuolella. Englanniksi se on vain yksi keskihajonta keskiarvon yläpuolella. Se kertoo, että matematiikassa pistemääräsi on paljon korkeampi kuin useimmilla opiskelijoilla (pistemääräsi putoaa häntään).
näiden tietojen perusteella suoriuduit itse asiassa paremmin matematiikassa kuin englanniksi!

Todennäköisyyskysymykset, joissa käytetään standardimallia

kysymykset normaalijakauman todennäköisyydestä voivat näyttää hälyttäviltä, mutta niiden ratkaisemisen avain on sen ymmärtäminen, mitä tavallisen normaalijakauman alla oleva pinta-ala edustaa. Tavallisen normaalijakaumakäyrän alittava kokonaispinta-ala on 100% (eli ”1” desimaalina). Esimerkiksi käyrän vasen puolisko on 50% eli .5. Käyrän vasemmassa puoliskossa esiintyvän satunnaismuuttujan todennäköisyys on siis .5.

kaikki ongelmat eivät tietenkään ole aivan niin yksinkertaisia, minkä vuoksi on olemassa z-taulukko. Kaikki z-taulukko ei mittaa näitä todennäköisyyksiä (eli 50%) ja laittaa ne keskihajonnat keskiarvosta. Keskiarvo on normaalin normaalijakauman keskellä, ja todennäköisyys 50% vastaa Nollaa keskihajonnaa.

normaali normaalijakauma: kuinka löytää todennäköisyys (vaiheet)

Vaihe 1: Piirrä kellokäyrä ja varjo sille alueelle, jota kysymyksessä kysytään. Alla olevassa esimerkissä Z >-0.8. Tämä tarkoittaa, että etsit todennäköisyys, että z on suurempi kuin -0.8, joten sinun täytyy piirtää pystysuora viiva -0.8 keskihajonta keskiarvosta ja varjosta kaikkea, mikä on tuota lukua suurempi.

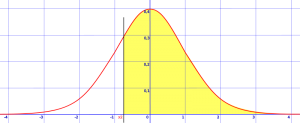
varjostettu alue on z > -0,8

Vaihe 2: Käy normaalin todennäköisyysalueen indeksissä ja etsi kuva, joka näyttää graafiltasi. Seuraa ohjeita, että sivu löytää z-arvo kuvaajan. Z-arvo on todennäköisyys.

Vihje: Vaihe 1 on teknisesti valinnainen, mutta todennäköisyyssanaongelmiin on aina hyvä piirtää kuvaaja. Tämä johtuu siitä, että useimmat virheet eivät tapahdu siksi, että et voi tehdä matematiikkaa tai lukea z-taulukkoa, vaan koska vähennät Z-pisteet lisäämisen sijaan (eli kuvittelet todennäköisyyden käyrän alle väärään suuntaan. Sketsi auttaa sementoimaan päähäsi juuri sen, mitä etsit.

Jos sinulla on vielä ongelmia, tutustu tuutoreihin osoitteessa Chegg.com. ensimmäinen 30 minuuttia live tutor on ilmainen!

normaalijakauman Sanaongelmat

Tämä video näyttää yhden esimerkin normaalijakauman sanaongelmasta. Lisää esimerkkejä, lue alla:

kun taklataan normaalijakaumaa tilastoluokassa, yritetään löytää kaaren alle jäävä alue. Kokonaispinta-ala on 100% (desimaalina, eli 1). Normaalijakeluongelmia on kuudessa perustyypissä. Mistä tietää, että sanaongelmaan liittyy normaalijakelu? Etsi avainlausetta ” oletetaan muuttujan jakautuvan normaalisti ”tai” oletetaan muuttujan olevan suunnilleen normaali.”Ratkaistaksesi sanaongelman sinun täytyy selvittää, mitä tyyppiä sinulla on.

1. ”välissä”: Sisältää lause ” välillä ”ja sisältää ylärajan ja alarajan (eli”etsi talojen määrä hinnoiteltu välillä $50k ja 200k”).
2. ”yli” tai ”yli”: sisältävät lauseen ”yli” tai ”yli”.
3. ”vähemmän kuin”.
4. Lower Cut Off Example (video)
5. Middle procent Example (video)
6. Middle procent Example (video)

”Between”

Tämä ohje kattaa sellaisten ongelmien ratkaisemisen, jotka sisältävät lauseen ”between” ja sisältävät ylä-ja alarajan (eli ”etsi 50-200 K dollarin hintaisten talojen lukumäärä”. Huomaa, että tämä on erilainen kuin löytää ”keskimmäinen prosenttiosuus” jotain.

normaalijakauman sanaongelmat: ”välillä”: vaiheet

Vaihe 1: Tunnista sanan ongelma osat. Sanaongelma tunnistaa:

1. keskiarvon (keskiarvo tai μ).
2. keskihajonta (σ).
3. numero valittu (eli ”valitse yksi sattumanvaraisesti” tai ”valitse kymmenen sattumanvaraisesti”).
4. X: ”välillä” (eli ”5 000-10 000 dollarin välillä” olisi X 5 000 ja 10 000 dollarin välillä).

lisäksi sinulle annetaan joko:

1. otoskoko (eli 400 taloa, 33 henkilöä, 99 tehdasta, 378 putkimiestä jne.). Tai
2. sinulta saatetaan kysyä todennäköisyyttä (jolloin otoskokosi on todennäköisimmin jokainen, eli ”Journeyman plumbers” tai ”First year pilots.”

Vaihe 2: piirrä kaavio. Laita vaiheessa 1 tunnistamasi keskiarvo keskelle. Laita numero liittyy ”välillä” kaaviossa (ottaa arvata, missä numerot putoaisivat–sen ei tarvitse olla tarkka). Esimerkiksi jos keskiarvosi oli 100 dollaria, ja sinulta kysyttiin ”tuntipalkat 75-125 dollaria”) kuvaajasi näyttää jokseenkin tältä:

Vaihe 3: Selvitä Z-pisteet. Kytke ensimmäinen X arvo (minun kuvaaja edellä, se on 75) osaksi z arvo kaava ja ratkaista. Μ (keskiarvo), on 100 otosdiagrammista. Voit saada nämä luvut (mukaan lukien σ, keskihajonta) vastauksistasi vaiheessa 1 :

*huomaa: jos kaava hämmentää, kaikki tämä kaava pyytää tekemään:
1. vähennä keskiarvo X: stä
2. Jaa keskihajonnalla.

Vaihe 4: Toista vaihe 3 toiselle X: lle.

Vaihe 5: Ota numerot vaiheista 3 ja 4 ja etsi niiden avulla alue z-taulukosta.

Jos sinua pyydettiin löytämään todennäköisyys kysymykseesi, siirry vaiheeseen 6a. jos sinua pyydettiin löytämään numero tietystä otoskoosta, siirry vaiheeseen 6b.

vaihe 6a:

Muunna vastaus vaiheesta 5 prosentiksi.

esimerkiksi 0, 1293 on 12, 93%.

That ’ s it–skip step 6b!

vaihe 6b

kerro otoskoko (joka löytyy vaiheesta 1) vaiheesta 4 löytämälläsi z-arvolla. Esimerkiksi 0,300 * 100 = 30.

That ’ s it!

”yli” tai ”yli”

Tämä ohje kattaa normaalijakauman ongelmien ratkaisemisen, joka sisältää lauseen ”yli” (tai lauseen, kuten ”yllä”).

Vaihe 1: Jaa sana ongelma osiin. Löytää:

1. keskiarvo (keskiarvo tai μ)
2. keskihajonta (σ)
3. luku (esimerkiksi ”Valitse viisikymmentä satunnaisesti” tai ”valitse 90 satunnaisesti”)
4. X: luku, joka liittyy ”vähemmän kuin” – lauseeseen. Esimerkiksi, jos sinua pyydettiin löytämään ”alle $9,999” niin X on 9,999.

Vaihe 2: Etsi otos ongelmasta. Sinulla on joko tietty koko (kuten ”1000 televisiot”) tai yleinen näyte (”jokainen televisio”).

Piirrä kuva, Jos ongelma on keskiarvo ja alue, jota etsit. Esimerkiksi jos keskiarvo on 15 dollaria, ja sinua pyydettiin selvittämään mitkä illalliset maksavat yli 10 dollaria, graafisi saattaa näyttää tältä:

Vaihe 3: Laske Z-pisteet (liitä arvosi z arvo kaava ja ratkaista). Käytä vastauksia vaiheesta 1 :

periaatteessa kaavalla vain vähennetään keskiarvo X: stä ja jaetaan sitten tuo vastaus keskihajonnalla.

Vaihe 4: Etsi alue Z-pisteellä vaiheesta 3. Käytä z-pöytää. Etkö ole varma miten lukea z-taulukko? Katso video z-pöydän sivulta.

Vaihe 6: siirry vaiheeseen 6a löytääksesi todennäköisyyden tai siirry vaiheeseen 6b laskeaksesi tietyn luvun tai määrän.

vaihe 6a
Käännä vaiheen 5 vastaus prosentiksi.

esimerkiksi 0, 1293 on 12, 93%.

Skip step 6b: you ’ re done!

vaihe 6b
kerrotaan näytteen koko vaiheesta 1 Z-pisteellä vaiheesta 4. Esimerkiksi 0,500 * 100 = 50.

olet valmis!

alle

Tämä how-to kattaa normaalijakauman sanaongelmien ratkaisemisen, joissa on lause ”vähemmän kuin” (tai vastaava lause, kuten ”vähemmän kuin”).

normaalijakauman sanaongelmat alle: vaiheet

Vaihe 1: Jaa sanaongelma osiin:

1. keskiarvo (keskiarvo tai μ)
2. keskihajonta (σ)
3. valittu luku (ts. ”choose one at random ”tai”select ten at random”)
4. X: luku, joka menee” alle ”(eli” alle 99 000 dollaria”, listaisi X: n 99 000: ksi)

Plus, sinulla on joko:

1. tietty otoskoko. Esimerkiksi 500 venettä, 250 voileipää, 100 televisiota jne.
2. kaikki otoksessa (sinua pyydetään löytämään todennäköisyys). Esimerkiksi ”ensimmäisen vuoden lääketieteen opiskelijat”, ”syöpäpotilaat” tai ” lentäjät.”

Vaihe 2: Piirrä kuva, joka auttaa hahmottamaan ongelman. Seuraavassa kuvaajassa keskiarvo on 15 ja pinta-ala ”alle 4”):

Vaihe 3: Etsi z-arvo liittämällä annetut arvot kaavaan. Otosdiagrammimme ” X ” on 4 ja μ (eli keskiarvo) on 15. Voit saada nämä luvut (myös σ, keskihajonta) vastauksistasi vaiheessa 1, jossa tunnistit ongelman osat:

kaikki mitä sinun tarvitsee tehdä ratkaistaksesi kaavan on:

1. vähennä keskiarvo X: stä.
2. Jaa keskihajonnalla.

Vaihe 4: Ota numero vaiheesta 3 ja etsi alue z-taulukon avulla.

Vaihe 5:todennäköisyyden löytämiseksi siirrytään vaiheeseen 6a. luvun löytämiseksi tietystä otoskoosta siirrytään vaiheeseen 6b.

vaihe 6a

muuta luku vaiheesta 5 prosentiksi.

esimerkiksi 0, 1293 on 12, 93%.

That ’ s it!

vaihe 6b

kerro otoskoko (joka löytyy vaiheesta 1) vaiheesta 4 löytämälläsi z-arvolla. Esimerkiksi 0,300 * 100 = 30.

That ’ s it!

alempi leikkaus

joskus normaalijakauman sanaongelmasta pyydetään etsimään ”ylemmän prosenttimäärän alaraja” jostakin (eli ”etsi Katkaisupiste läpäistäksesi tietyn kokeen, jossa ylempi 40% testin ottajista läpäisee”). Alempi Katkaisupiste on piste, jossa pisteet jäävät kyseisen pisteen alapuolelle. Kannattaa esimerkiksi selvittää, missä kohtaa karsintapiste on alimmalla 10 prosentilla testin ottajista.

Katso YouTube-kanavallamme lisää toimivia ongelmia.

Normaalijakauma TI 89 esimerkkiä

alkeistilastoissa on usein kysymys, jossa kysytään katkaisupisteitä tietylle prosentille normaalijakaumasta, kuten top 90% tai top 10%. Vaikka tällaisten ongelmien selvittäminen käsin on hankalaa, TI-89-grafiikkalaskuri tekee kevyttä työtä löytääkseen huippuprosentin katkaisupisteet käänteisellä Normaalitoiminnolla. Mitä olet todella tekemässä on etsivät cut off pistettä tietyn prosenttipisteen: jos sinulla on esimerkiksi lista arvosanoista ja haluat tietää, mikä pistemäärä on 99.prosenttipisteessä, voit käyttää käänteistä normaalifunktiota löytääksesi tuon prosenttirajan.

Finding Cut Off Points for a Top prosent

Sample problem: Students at a certain college average 5 feet 8 inches (68 inches) tall. Korkeudet jaetaan normaalisti, keskihajonta on 2,5 tuumaa. Mikä on arvo, joka erottaa ylimmän 1% korkeuksista muusta väestöstä?

Vaihe 1: Paina sovelluksia ja käytä vieritysnäppäimiä korostaaksesi Stats / List editoria.

Vaihe 2: Paina F5 2 1 (Näin pääset käänteiseen normaaliin näyttöön).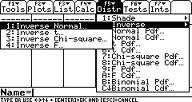

Vaihe 3: Kirjoita 0, 99 alueruutuun.

Vaihe 4: μ-ruutuun merkitään 68.

Vaihe 5: merkitään 2.5 σ-ruutuun.

Vaihe 6: Paina ENTER.

Vaihe 7: Lue tulokset: Inverse=73.8159 tarkoittaa, että 99.prosenttipisteen leikkauskorkeus on 73.8159 tuumaa.

That ’ s it!

Todennäköisyysosuusesimerkki (NormalCDF-funktio)

Otoskysymys: Ryhmä opiskelijoita, joilla on normaalisti jaettu palkat ansaitsevat keskimäärin $6,800 keskihajonta $2,500. Mikä osuus opiskelijoista tienaa 6 500-7 300 dollaria?

Vaihe 1: Paina sovelluksia. Vieritä Stats/List Editor ja paina ENTER.

Vaihe 2: paina F5 4.

Vaihe 3: merkitään 6500 ala-arvo-ruutuun.

Vaihe 4: merkitään 7300 ylempään arvo-ruutuun.

vaihe 5: merkitään 6800 μ-ruutuun.

Vaihe 6: σ-ruutuun merkitään 2500. Paina ENTER.

Vaihe 7: Lue vastaus. Cdf=.127018. Toisin sanoen, .013 eli 13 prosenttia opiskelijoista tienaa 6 500-7 300 dollaria.

TI-89 piirtää Normaalijakaumakäyrän

TI-89 ei voi vain laskea z-pistemääriä ja palautusarvoja normaalijakaumille, se voi myös piirtää normaalijakaumakäyrän. Normaalijakauman kuvaaminen voi auttaa sinua näkemään, mitä sinun pitäisi etsiä, ja antaa sinulle vielä yhden työkalun normaalijakauman ongelmien ratkaisemiseen. TI-89 voi piirtää normaalijakaumakäyrän, jonka pinta-ala on varjostettu mille tahansa arvolle. Voit esimerkiksi luoda kaavion, joka on: pienempi kuin tietty määrä, suurempi kuin tietty määrä tai-välillä tietyn joukon numeroita.

Otosongelma: Piirrä normaalijakaumakäyrä opiskelijoiden palkoille tyypillisen lukukauden aikana. Opiskelijoiden palkkojen keskiarvo on 6 800 dollaria ja keskihajonta 2 500 dollaria. Varjosta kaaviossa oleva alue, joka vastaa palkkoja 7 300-9 000 dollarin välillä.

Vaihe 1: Paina sovelluksia ja valitse Stats / List Editor.

Vaihe 2: Paina F2 3 ja F2 4.

Vaihe 3: Paina F5) 1.

Vaihe 4: selaa alaspäin ja kirjoita 7300 ala-arvo-ruutuun.

Vaihe 5: selaa alaspäin ja kirjoita 9000 ylempään arvo-ruutuun.

Vaihe 6: selaa alaspäin ja kirjoita 6800 μ-ruutuun.

Vaihe 7: selaa alaspäin ja kirjoita σ-ruutuun 2500.

Vaihe 8: vieritä alaspäin. Käännä Auto asteikko ”Kyllä” painamalla oikeaa vieritysnäppäintä, sitten alas vieritysnäppäintä valita kyllä. Paina ENTER.

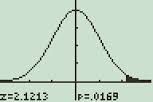
TI-89-laskurissa näkyvä normaalijakauman kuvaaja.

That ’ s it!

kärki: Jos haluat syöttää∞: n (infinity) yhdeksi alemmista tai ylemmistä arvoistasi, paina timanttinäppäintä ja luetteloi sitten.

Beyer, W. H. CRC Standard Mathematical Tables, 28. Boca Raton, FL: CRC Press, s. 533 & ndash; 534, 1987.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3.toim. New York: Wiley, 1968.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2.toim. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” The Error Curve.”§6.4 in Mathematical Recreations. New York: W. W. Norton, s. 121 & ndash; 123, 1942.
Patel, J. K. Ja Read, C. B. Handbook of the Normal Distribution. New York: Dekker, 1982.

1. mikä on 68-95-99, 7-sääntö?
2. Box Cox-muunnos
3. Box Muller-muunnos
4. Gaussin Sekoitusmallit.
5. mikä on normaali Todennäköisyyslaskenta?
6. miten Z-pisteet lasketaan tilastoissa
7. Etsi Z-pistemäärän oikealla puolella oleva alue.
8. käyttäen normaalia likiarvoa Binomiongelman ratkaisemiseen
9. mikä on jatkuvuuden korjauskerroin?
10. Normaalijakaumakäyräindeksin alle jäävä alue
11. keskeinen raja-arvolause.
12. vääristynyt Normaalijakauma.
13. Kaksihäntäinen Normaalikäyrä.
14. Q-funktio.

——————————————————————————

Tarvitsetko apua läksy-tai koekysymyksessä? Chegg Studyn avulla saat askelmittaisia ratkaisuja kysymyksiisi alan asiantuntijalta. Ensimmäinen 30 minuuttia Chegg tutor on ilmainen!