Scalenen kolmio on kolmio, jonka kaikki sivut ovat eripituisia.
kaikki kulmat ovat myös erilaisia.
joten yksikään sivu ei ole yhtä suuri eikä yksikään kulma ole yhtä suuri.
Scaleenin kolmion pinta-alan kaava :
= √
missä
s = (a + b + c)/2
tässä A, b ja C ovat kolmion sivun pituuksia.
käytännön ongelmat
ongelma 1:
Etsi scalenen kolmion pinta-ala, jonka sivujen pituus on 12 cm, 18 cm ja 20 cm.
ratkaisu :
koska kolmen sivun pituudet ovat erilaiset, kolmio on scalene-kolmio.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25 x 13 x 7 x 5)
= 5√455
joten annetun scalenen kolmion pinta-ala on 5 √455 neliösenttimetriä.
ongelma 2 :
skaleenikolmion sivut ovat 12 cm, 16 cm ja 20 cm. Etsi korkeus pisimmälle sivulle.
ratkaisu :
jotta löytäisimme korkeuden kolmion pisimmälle sivulle, on ensin löydettävä kolmion pinta-ala.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
koska haluamme löytää korkeuden pisimmälle sivulle, pisin sivu on kolmion pohja kuten alla on esitetty.
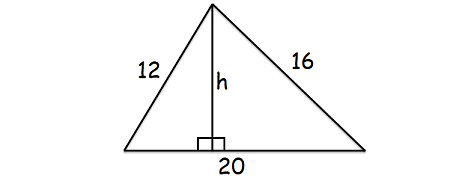
tässä pisin sivu on 20 cm.
yllä olevan kolmion alue = 96 cm2
(1/2) x 20 x h = 96
10h = 96
Jaa kumpikin puoli 10: llä.
h = 9,6 cm
joten korkeutta pisimmälle sivulle on 9,6 cm.
ongelma 3:
skaleenikolmion sivut ovat suhteessa (1/2) : (1/3) : (1/4). Jos kehä on 52 cm, sitten löytää pituus pienin sivu.
ratkaisu :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length pienin sivu on 12 cm.
ongelma 4 :
scalenen kolmion pinta-ala on 216 cm2 ja sivut ovat suhteessa 3 : 4 : 5. Etsi kokoisen kolmion.
ratkaisu :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
annetun skaleenikolmion ympärysmitta on
= 18 + 24 + 30
= 72 cm
ongelma 5 :
suorakulmaisen skaleenikolmion toinen sivu on kaksi kertaa toinen,ja hypotenuusa on 10 cm. Etsi alueen kolmio.
ratkaisu :
olkoon ” x ” kolmion yhden jalan pituus.
silloin toisen jalan pituus on 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2) (x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

edellä annettujen asioiden lisäksi, jos tarvitset jotain muuta matematiikassa, käytä google custom-hakua tästä.
jos sinulla on palautetta matikkasisällöstämme, lähetä meille sähköpostia:
arvostamme aina palautetta.
voit myös käydä seuraavilla sivuilla eri asioista matematiikassa.
SANAONGELMAT
HCF-ja LCM-sanaongelmat
Sanaongelmat yksinkertaisissa yhtälöissä
sanaongelmat lineaarisissa yhtälöissä
Sanaongelmat neliöyhtälöissä
algebran sanaongelmat
sanaongelmat junissa
alue-ja kehäsanaongelmat
Word Problems on direct variation and Inverse variation
word problems on Unit Price
word problems on Unit rate
word problems on Unit rate
word problems on comparing rates
converting usual units word problems
converting usual units word ongelmat
Sanaongelmat yksinkertaisesta korosta
sanaongelmat kertyneestä korosta
Sanaongelmat kulmatyypeistä
täydentäviä ja täydentäviä kulmia sanaongelmat
Tuplafaktat sanaongelmat
trigonometriset sanaongelmat
Prosenttisanaongelmat
voitto-ja tappiosan ongelmat
Markup ja Markdown sanaongelmat
desimaalisanaongelmat
sanaongelmat murtoluvuilla
Sanaongelmat sekamurtoluvuilla
yhden askeleen yhtälö sanaongelmat
lineaarinen epätasa-arvo sanaongelmat
suhde ja osuus sanaongelmat
ajan ja työn sanaongelmat
sanaongelmat sarjoissa ja venn-diagrammeissa
Sanaongelmat ikäluokissa
Pythagoraan lauseen sanaongelmat
prosenttia lukusanaongelmista
sanaongelmat vakionopeudessa
Sanaongelmat keskinopeudessa
Sanaongelmat kolmion kulmien summassa on 180 astetta
muut aiheet
voitto-ja tappio-oikotiet
prosenttiosuus-Oikotiet
Aikataulukon pikanäppäimet
aika -, nopeus-ja etäisyysnäppäimet
suhde-ja suhteellisuusnäppäimet
toimialue ja rationaalifunktioiden alue
Domain ja rationaalifunktioiden alue, jossa on reikiä
Graafiset rationaalifunktiot
Graafiset rationaalifunktiot reikineen
muuntamalla toistuvat desimaalit murtoluvuiksi
rationaalilukujen Desimaaliesitys
neliöjuuren löytäminen pitkäjakolla
L. C.M-menetelmä aika-ja työongelmien ratkaisemiseksi
sanan ongelmien kääntäminen algebrallisiksi lausekkeiksi
jäljellä kun 2 potenssi 256 jaetaan 17: llä
jäljellä kun 17 potenssi 23 jaetaan 16: lla
kaikkien kolminumeroisten lukujen summa jaollinen 6: lla
kaikkien kolminumeroisten lukujen summa jaollinen 7: llä
summa kaikki kolminumeroiset luvut jaollisia 8: lla
kaikkien 1, 3, 4: llä muodostettujen kolminumeroisten lukujen summa
kaikkien kolmen nelinumeroisen luvun summa, jotka on muodostettu muilla kuin nollanumeroilla
kaikkien kolmen nelinumeroisen luvun summa, jotka on muodostettu 0, 1, 2, 3: lla
kaikkien kolmen nelinumeroisen luvun summa, jotka on muodostettu käyttäen 1, 2, 5, 6