3.3 Le cycle de Carnot | Maybaygiare.org

Suivant: 3.4 Réfrigérateurs et Chauffe: 3. La Première Loi Précédente: 3.2 Représentation généralisée de l’Indice de Contenu

Un cycle de Carnot est représenté sur la Figure 3.4. Il aquatre processus. Il y a deux jambes réversibles adiabatiques et deux jambes réversibles isothermes. Nous pouvons construire un cycle de Carnot avec de nombreux systèmes différents, mais les concepts peuvent être montrés en utilisant un fluide de travail familier, le gaz idéal. Le système peut être considéré commeune chambre fermée par un piston et remplie de ce gaz idéal.

Figure 3.4: Cycle de Carnot diagram diagramme thermodynamique à gauche et schéma des différentes étapes du cycle pour un système composé d’un gaz idéal à droite

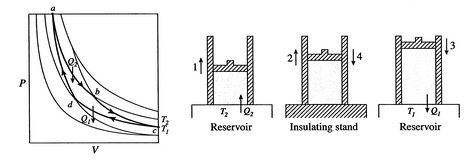
Les quatre processus du cycle de Carnot sont:

Le système est à la température 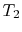à l’état . Il est mis en contact avec un réservoir de chaleur, qui n’est qu’une masse liquide ou solide suffisamment étendue pour que sa température ne change pas sensiblement lorsqu’une certaine quantité de chaleur est transférée au système. En d’autres termes, le réservoir de chaleur est une température constantesource (ou récepteur) de chaleur. Le système subit ensuite anisothermal expansion de de , avec la chaleur absorbée à l’ .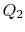
Atstate , le système est isolé thermiquement (retiré du contact avec le réservoir de chaleur), puis laissez s’étendre jusqu’à . Pendant cette expansion, la température diminue jusqu’à . L’échange de chaleur pendant cette partie du cycle, $Q_{bc}=0.$ )
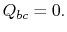À l’état le système est mis en contact avec un réservoir de chaleur à température . Il est ensuite compressé à l’état 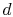, rejetant la chaleur 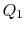dans le processus.
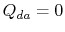Enfin, le système est compressé adiabatiquement à l’état initial . L’échange de chaleur $QQ_{da}=0$ .

L’efficacité thermique du cycle est donnée par la définition

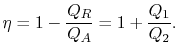$\displaystyle\eta=1-\frac{Q_R}{Q_A}= 1+\frac{Q_1}{Q_2}.$

(3..4)

Dans cette équation, il y a une convention de signe implicite. Les quantités , telles que définies sont les grandeurs de la chaleur absorbée et injectée. Les quantités , en revanche sont définies en référence à la chaleur reçue par le système. Dans cet exemple, l’ancien est négatif et ce dernier est positif. La chaleur absorbée et injectée par le système a lieu lors de processus isothermes et nous savons déjà quelles sont leurs valeurs d’Eq.(3.1):

$\displaystyle Q_2= W_{ab}= N\mathbf{R}T_2,$

$$\displaystyle Q_1=W_{cd}= N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\quad\textrm {(QQ_1 is est négatif.)}}$

L’efficacité peut maintenant être écrite en termes de volumes aux différents états comme

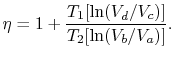$\displaystyle\eta=1+\frac{T_1}{T_2}.$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) montre deux conséquences. Tout d’abord, les chaleurs reçues et rejetées sont liées aux températures des parties isothermes du cycle par

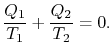$\displaystyle\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0.$

(3..6)

Deuxièmement, l’efficacité d’un cycle de Carnot est donnée de manière compacte par

$\displaystyle\eta=1-\frac { T_1} {T_2}.\qquad\textbf { Efficacité du cycle de Carnot.}$

(3..7)

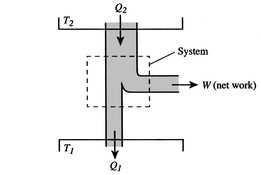
L’efficacité ne peut être de 100% que si la température à laquelle la chaleur est rejetée est nulle. Les transferts de chaleur et de travail vers et depuis le système sont schématisés en figure 3.5.

Figure 3.5:Le travail et les transferts de chaleur ina cycle de Carnot entre les deux réservoirs de chaleur

Boueux Points

Depuis $\eta = 1- {T_1}/{T_2}$ , en regardant le graphique, doesthat dire les plus éloignés de la isothermes sont, thegreater efficacité? Et que s’ils étaient très proches, ce seraittrès inefficace? (MP 3.2)

Dans le cycle de Carnot, pourquoi ne traitons-nous que des changements de volume et pas des changements de pression sur les adiabates et les isothermes?(MP 3.3)

Existe-t-il une application physique pour le cycle de Carnot ? Peut-on concevoir un moteur Carnot pour un dispositif de propulsion ?(MP 3.4)

Comment savons-nous quels cycles utiliser comme modèles pour des processus réels?(MP 3.5)

Suivant: 3.4Réfrigérateurs et Chauffer: 3. La Première Loi Précédente: 3.2 Représentation généralisée de l’Index des contenus

UnifiedTP

Maybaygiare.org

Laisser un commentaire Annuler la réponse