Le triangle scalène est un triangle avec tous les côtés de longueurs différentes.
Tous les angles sont également différents.
Donc, aucun côté n’est égal et aucun angle n’est égal.
Formule pour l’aire du triangle scalène :
= √
où
S=(a +b + c) /2
Ici a, b et c sont des longueurs latérales du triangle.
Problèmes de pratique
Problème 1:
Trouvez l’aire du triangle scalène dont la longueur des côtés est de 12 cm, 18 cm et 20 cm.
Solution:
Parce que les longueurs des trois côtés sont différentes, le triangle est un triangle scalène.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
=√
= √(25 x 13 x 7 x 5)
=5√455
Ainsi, l’aire du triangle scalène donné est de 5 √455 cm carrés.
Problème 2:
Les côtés d’un triangle scalène sont de 12 cm, 16 cm et 20 cm. Trouvez l’altitude du côté le plus long.
Solution:
Pour trouver l’altitude du côté le plus long d’un triangle, nous devons d’abord trouver l’aire du triangle.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
=96 cm2
Parce que nous voulons trouver l’altitude du côté le plus long, le côté le plus long sera la base du triangle comme indiqué ci-dessous.
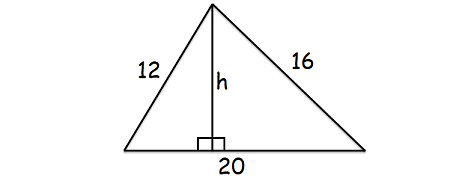
Ici, le côté le plus long mesure 20 cm.
Aire du triangle ci-dessus = 96 cm2
(1/2) x 20 x h= 96
10h=96
Divisez chaque côté par 10.
h= 9,6 cm
Ainsi, l’altitude du côté le plus long est de 9,6 cm.
Problème 3 :
Les côtés d’un triangle scalène sont dans le rapport (1/2) : (1/3) : (1/4). Si le périmètre est de 52 cm, trouvez la longueur du plus petit côté.
Solution :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length du plus petit côté est de 12 cm.
Problème 4:
L’aire du triangle scalène est de 216 cm2 et les côtés sont dans le rapport 3:4:5. Trouvez le périmètre du triangle.
Solution :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x=18
4x=24
5x=30
Le périmètre du triangle scalène donné est
= 18 + 24 + 30
=72 cm
Problème 5:
Un côté d’un triangle scalène à angle droit est deux fois l’autre et l’hypoténuse est de 10 cm. Trouvez l’aire du triangle.
Solution :
Soit « x » la longueur d’une des jambes du triangle.
Ensuite, la longueur de l’autre jambe est 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2)(x)(2x)
= (1/2)(2√5)(4√5)
=20 cm2

En dehors des choses données ci-dessus, si vous avez besoin d’autres choses en mathématiques, veuillez utiliser notre recherche personnalisée Google ici.
Si vous avez des commentaires sur notre contenu mathématique, veuillez nous envoyer un e-mail:
Nous apprécions toujours vos commentaires.
Vous pouvez également visiter les pages Web suivantes sur différentes choses en mathématiques.
PROBLÈMES DE MOTS
Problèmes de mots HCF et LCM
Problèmes de mots sur des équations simples
Problèmes de mots sur des équations linéaires
Problèmes de mots sur des équations quadratiques
Problèmes de mots d’algèbre
Problèmes de mots sur les trains
Problèmes de mots sur les aires et les périmètres
Problèmes de mots sur la variation directe et la variation inverse
Problèmes de mots sur le prix unitaire
Problèmes de mots sur le taux unitaire
Problèmes de mots sur la comparaison des taux
Conversion d’unités usuelles problèmes de mots
Conversion d’unités métriques Mot problèmes
Problèmes de mots sur les intérêts simples
Problèmes de mots sur les intérêts composés
Problèmes de mots sur les types d’angles
Problèmes de mots d’angles complémentaires et supplémentaires
Problèmes de mots doubles faits
Problèmes de mots de trigonométrie
Problèmes de mots de pourcentage
Problèmes de mots de profit et de perte
Problèmes de mots markdown
Problèmes de mots décimaux
Problèmes de mots sur les fractions
Problèmes de mots sur les fractrions mixtes
Problèmes de mots d’équation en une étape
Inégalités linéaires problèmes de mots
Rapport et problèmes de mots de proportion
Problèmes de mots de temps et de travail
Problèmes de mots sur les ensembles et les diagrammes de venn
Problèmes de mots sur les âges
Problèmes de mots du théorème de Pythagore
Pourcentage d’un nombre de problèmes de mots
Problèmes de mots sur la vitesse constante
Problèmes de mots sur la vitesse moyenne
Problèmes de mots sur la somme des angles d’un triangle est de 180 degrés
AUTRES SUJETS
Raccourcis de profit et de perte
Raccourcis de pourcentage
Raccourcis de tableau des temps
Raccourcis de temps, de vitesse et de distance
Raccourcis de ratio et de proportion
Domaine et gamme de fonctions rationnelles
Domaine et gamme de fonctions rationnelles avec des trous
Représentation graphique de fonctions rationnelles
Représentation graphique de fonctions rationnelles avec des trous
Conversion de décimales répétées en fractions
Représentation décimale de nombres rationnels
Trouver la racine carrée en utilisant la division longue
L.C.Méthode M pour résoudre des problèmes de temps et de travail
Traduire les problèmes de mots en expressions algébriques
Reste lorsque 2 puissances 256 sont divisées par 17
Reste lorsque 17 puissances 23 sont divisées par 16
Somme des nombres à trois chiffres divisibles par 6
Somme des nombres à trois chiffres divisibles par 7
Somme de tous les nombres à trois chiffres divisibles par 7
nombres à trois chiffres divisibles par 8
Somme des nombres à trois chiffres formés en utilisant 1, 3, 4
Somme des trois nombres à quatre chiffres formés avec des chiffres non nuls
Somme des trois nombres à quatre chiffres formés en utilisant 0, 1, 2, 3
Somme des trois nombres à quatre chiffres formés en utilisant 1, 2, 5, 6