J’ai déjà discuté de la régression linéaire sur ce blog, mais très souvent, une ligne droite n’est pas la meilleure façon de représenter vos données. Pour ces situations spécifiques, nous pouvons tirer parti de certains des outils disponibles pour effectuer une régression non linéaire ou un ajustement de courbe dans Excel.
Tu te souviens de notre vieil ami LINEST? Bien que LINEST soit l’abréviation de « linear estimation”, nous pouvons également l’utiliser pour des données non linéaires avec quelques ajustements simples.
Disons que nous avons des données de chute de pression par rapport à. débit à travers une vanne d’eau, et après avoir tracé les données sur un graphique, nous voyons que les données sont quadratiques.
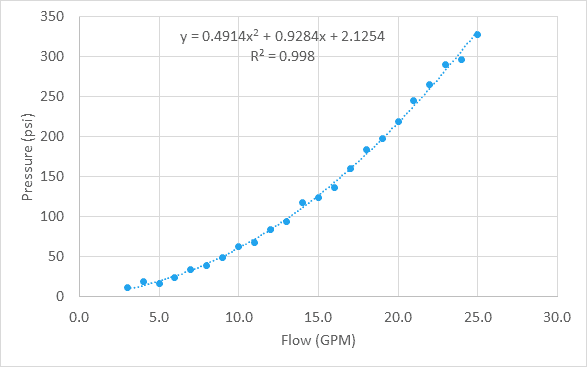
Même si ces données sont non linéaires, la fonction LA plus LINÉAIRE peut également être utilisée ici pour trouver la courbe d’ajustement la mieux adaptée à ces données. Pour une équation polynomiale, nous le faisons en utilisant des constantes de tableau.
Un avantage d’utiliser LINEST pour obtenir les coefficients qui définissent l’équation polynomiale est que nous pouvons renvoyer les coefficients directement aux cellules. De cette façon, nous n’avons pas à les transférer manuellement hors du graphique.
Puisque l’équation est quadratique, ou un polynôme du second ordre, il y a trois coefficients, un pour x au carré, un pour x et une constante. Nous devrons donc commencer par créer un espace pour stocker les trois coefficients de l’équation.
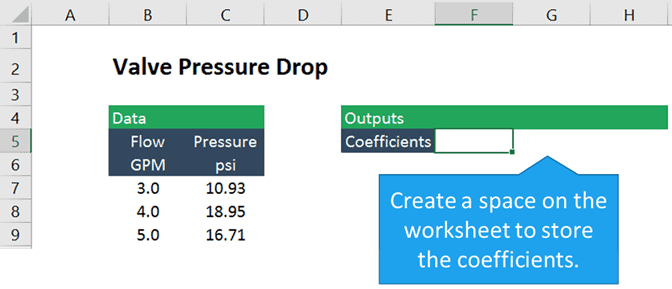
Utilisation de LINEST pour la régression non linéaire dans Excel
La fonction LINEST renvoie un tableau de coefficients et des statistiques de régression facultatives. Nous devrons donc l’entrer sous forme de formule de tableau en sélectionnant les trois cellules pour les coefficients avant d’entrer la formule.
Si les cellules contenant les données de débit et de pression sont nommées « débit” et « pression”, la formule ressemble à ceci:
=LINEST(pressure, flow^{1,2}, TRUE, FALSE)
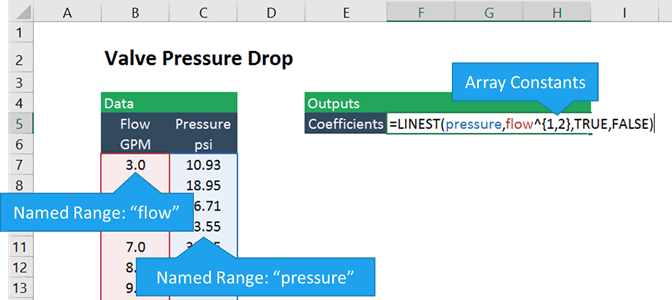
Les y connus dans ce cas sont les mesures de pression, et les x connus sont les mesures de débit mesures portées à la première et à la deuxième puissance. Les accolades, « { » et « } », indiquent une constante de tableau dans Excel. Fondamentalement, nous disons à Excel de créer deux tableaux: l’un de flow et l’autre de flow-squared, et d’adapter la pression à ces deux tableaux ensemble.
Enfin, les arguments TRUE et FALSE indiquent à la fonction la plus LINÉAIRE de calculer normalement l’ordonnée à l’origine (plutôt que de la forcer à zéro) et de ne pas renvoyer de statistiques de régression supplémentaires, respectivement.
Comme il s’agit d’une formule de tableau, nous devons la saisir en tapant Ctrl + Maj + Entrée.
La fonction renvoie alors les coefficients de x2 et x ainsi qu’une constante (car nous avons choisi d’autoriser LINEST à calculer l’ordonnée à l’origine).
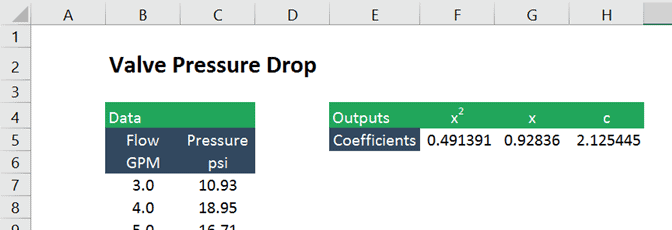
Les coefficients sont identiques à ceux générés par l’outil graphique de ligne de tendance, mais ils sont maintenant dans des cellules, ce qui les rend beaucoup plus faciles à utiliser dans les calculs ultérieurs.
Pour toute équation polynomiale, LINEST renvoie le coefficient pour l’ordre le plus élevé de la variable indépendante à l’extrême gauche, suivi du plus élevé suivant et ainsi de suite, et enfin la constante.
Une technique similaire peut également être utilisée pour l’ajustement de courbes exponentielles, logarithmiques et de fonctions de puissance dans Excel.
Ajustement d’une Courbe logarithmique aux Données
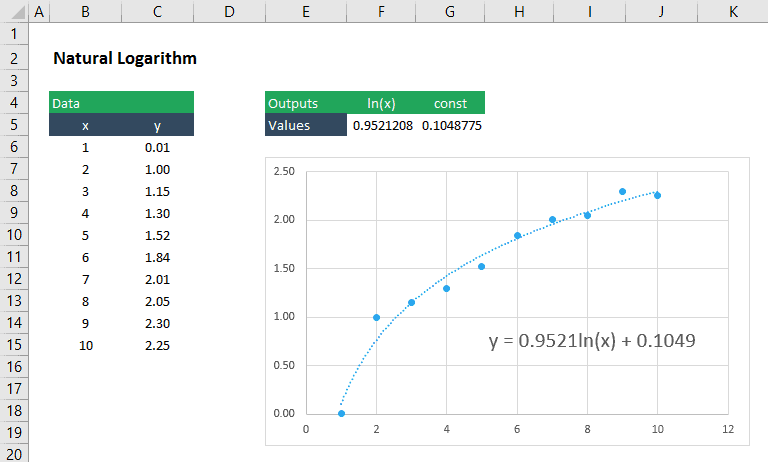
Une fonction logarithmique a la forme :

Nous pouvons toujours utiliser LINEST pour trouver le coefficient, m, et la constante, b, pour cette équation en insérant ln(x) comme argument pour les known_x:
= LINEST(y_values, ln(x_values), TRUE, FALSE)
Bien sûr, cette méthode s’applique à toute équation logarithmique, quel que soit le nombre de base. Il pourrait donc être appliqué à une équation contenant log10 ou log2 tout aussi facilement.
Trouver les Coefficients d’une Courbe Exponentielle la mieux adaptée
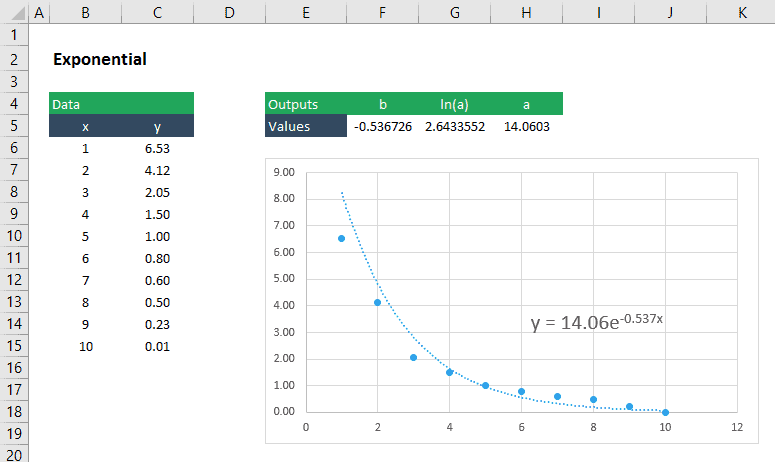
Une fonction exponentielle a la forme:
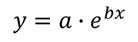
Il est un peu plus délicat d’obtenir les coefficients, a et b, pour cette équation car nous devons d’abord faire un peu d’algèbre pour que l’équation prenne une forme « linéaire”. Tout d’abord, prenez le journal naturel des deux côtés de l’équation pour obtenir ce qui suit:

Maintenant, nous pouvons utiliser LINEST pour obtenir ln(a) et b en entrant ln(y) comme argument pour les valeurs y:
= LINEST(ln(y_values), x_values, TRUE, FALSE)
La deuxième valeur renvoyée par cette formule de tableau est ln(a), donc pour obtenir juste « a”, nous utiliserions simplement la fonction exponentielle:

Ce qui, dans Excel, se traduit par:
=EXP(number)
Ajustement d’une fonction de puissance aux données
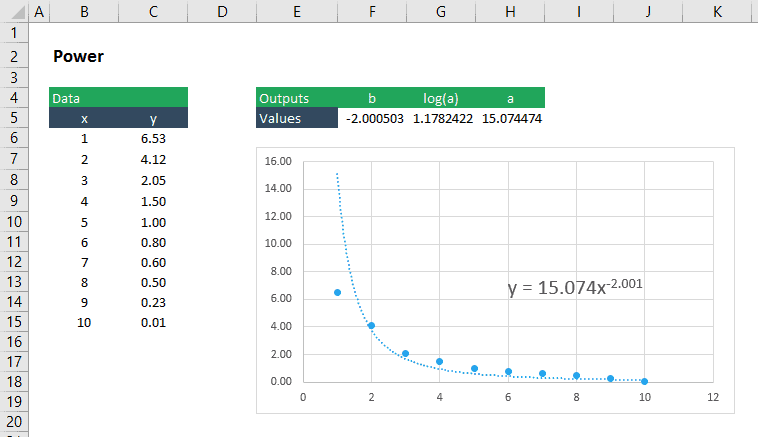
Une courbe de fonction de puissance peut être ajustée aux données en utilisant LINEST de la même manière que nous le faisons pour une fonction exponentielle. Une fonction de puissance a la forme:
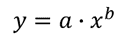
Encore une fois, nous pouvons le « linéariser” en prenant le log de base 10 des deux côtés de l’équation pour obtenir:
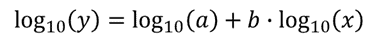
Avec l’équation sous cette forme, la fonction la plus LINÉAIRE pour renvoyer b et log10(a) peut être configurée comme suit:
= LINEST(LOG10(yvalues), LOG10(xvalues), TRUE, FALSE)
Puisque la fonction la PLUS LINÉAIRE renvoie b et log10(a), nous devrons trouver a avec la formule suivante:

Dans Excel, cette formule est:
= 10^(nombre)
C’est tout pour l’instant. Comme vous pouvez le voir, il existe plusieurs façons d’utiliser la fonction LINEST pour l’ajustement de courbes non linéaires dans Excel.