Expertise : Intermédiaire
Qu’est-ce qu’une fonction spline ?
Nous avons besoin de savoir quelles sont les caractéristiques essentielles des splines avant d’envisager comment construire un système de base pour elles.
Les fonctions splines sont formées en joignant des polynômes ensemble à des points fixesappelés nœuds. C’est-à-dire que l’on divise l’intervalle s’étendant de la limite inférieure tL à la limite supérieure tU sur laquelle on souhaite approximer une courbe en L+1 sous-intervalles séparés par L limites intérieures ξl appelées nœuds, ou parfois points d’arrêt.) Il y a une distinction entre ces deux termes, mais nous y reviendrons plus tard.
Considérons le cas le plus simple dans lequel un seul point d’arrêt divise l’intervalle en deux sous-intervalles. La fonction splinefunction est, dans chaque intervalle, un polynôme de degré spécifié (la puissance la plus élevée définissant le polynôme) ou d’ordre (le nombre de coefficients définissant le polynôme, qui est un de plus que son degré). Utilisons m pour désigner l’ordre du polynôme, de sorte quele degré est m-1:
Au point d’arrêt intérieur ξ1, les deux polynômes doivent se rejoindre en douceur. Dans le cas le plus courant, cela signifie que les dérivées correspondent à l’ordre un de moins que le degré. En fait, s’ils correspondaient à la dérivée dont l’ordre égalait le degré, ils seraient le même polynôme. Ainsi, une fonction spline définie dans ce was a un degré de liberté supplémentaire par rapport à un polynôme s’étendant sur tout l’intervalle.
Par exemple, que chaque polynôme soit un segment de droite, et donc de degré un. En cela, ils se rejoignent au point d’arrêt avec des dérivés correspondants jusqu’au degré 0; en bref, ils se rejoignent simplement et ont des valeurs identiques au point d’arrêt. Puisque le premier polynôme a deux degrés de liberté (pente et interception) et que le second, dont la valeur est déjà définie au point de rupture, n’a qu’un seul degré de liberté (pente), la ligne polygonale totale a troisdegrés de liberté.
En conséquence, si les deux polynômes sont des quadratiques, alors la correspondance à la fois en termes de valeurs et en termes de pente de la première dérivée à ξ1. Le premier polynôme a trois degrés de liberté, mais le second en perd deux car si la contrainte sur sa valeur et sa pente à ξi, et n’en conserve donc qu’un. Cela laisse un total de quatre degrés de liberté pour la fonction splinefonction formée de cette manière, comme opposé à trois pour un polynôme quadratique sur tout l’intervalle. La figure 1 montre les cas linéaires et quadratiques avec un seul point d’arrêt.
Quels sont quelques exemples de fonctions de base couramment utilisées?
On peut maintenant généraliser la situation à L points d’arrêt intérieurs, et une fonction spline étant d’ordre m ou de degré m-1 sur chaque sous-intervalle. Le premier segment polynomial a un complément complet de m degrés de liberté, mais chaque segment suivant n’a qu’un seul degré de liberté en raison des contraintes m-1 sur son comportement.Cela donne un total de L + m degrés de liberté, ou nombre de points d’arrêt intérieurs plus l’ordre des segments polynomiaux.
Ainsi, les fonctions splines sont essentiellement des généralisations de la notion de polygonallines. Ils acquièrent leur flexibilité de deux manières: d’une part, par l’ordre des polynômes à partir desquels ils sont construits, et d’autre part, par le nombre de points d’arrêt utilisés. Nous choisissons généralement de maintenir l’ordre fixe et d’ajouter des points d’arrêt nécessaires pour obtenir la flexibilité requise.
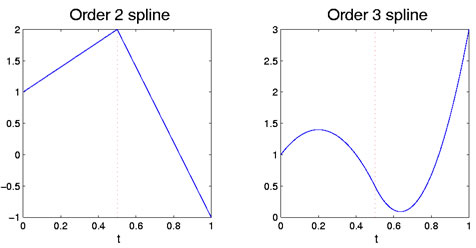
Figure 1: La figure de gauche montre une fonction spline d’ordre deux, quiest linéaire par morceaux. La figure de droite est une spline d’ordre 3, quiest quadratique par morceaux. Le point de rupture à 0,5 est indiqué par la ligne pointillée verticale rouge.