Les techniques de classification sont une partie essentielle des applications d’apprentissage automatique et d’exploration de données. Environ 70% des problèmes en science des données sont des problèmes de classification. Il existe de nombreux problèmes de classification, mais la régression logistique est courante et constitue une méthode de régression utile pour résoudre le problème de classification binaire. Une autre catégorie de classification est la classification multinomiale, qui gère les problèmes où plusieurs classes sont présentes dans la variable cible. Par exemple, IRIS dataset est un exemple très célèbre de classification multi-classes. D’autres exemples classent la catégorie article / blog / document.
La régression logistique peut être utilisée pour divers problèmes de classification tels que la détection de spam. Prédiction du diabète, si un client donné va acheter un produit particulier ou va-t-il désabonner un autre concurrent, si l’utilisateur cliquera sur un lien publicitaire donné ou non, et de nombreux autres exemples sont dans le seau.
La régression logistique est l’un des algorithmes d’apprentissage automatique les plus simples et les plus couramment utilisés pour la classification à deux classes. Il est facile à mettre en œuvre et peut être utilisé comme référence pour tout problème de classification binaire. Ses concepts fondamentaux de base sont également constructifs dans l’apprentissage profond. La régression logistique décrit et estime la relation entre une variable binaire dépendante et des variables indépendantes.
Dans ce tutoriel, vous apprendrez les choses suivantes en Régression Logistique:
- Introduction à la Régression Logistique
- Régression Linéaire Vs. Régression Logistique
- Estimation du Maximum de Vraisemblance Vs. Méthode des Moindres Carrés Ordinaires
- Comment fonctionne la Régression Logistique?
- Construction de modèles dans Scikit-learn
- Évaluation de modèles à l’aide d’une matrice de confusion.
- Avantages et inconvénients de la régression logistique
Régression logistique
La régression logistique est une méthode statistique pour prédire les classes binaires. Le résultat ou la variable cible est de nature dichotomique. Dichotomique signifie qu’il n’y a que deux classes possibles. Par exemple, il peut être utilisé pour des problèmes de détection du cancer. Il calcule la probabilité d’occurrence d’un événement.
C’est un cas particulier de régression linéaire où la variable cible est de nature catégorielle. Il utilise un journal des cotes comme variable dépendante. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
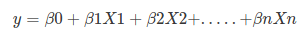
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
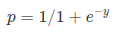
Apply Sigmoid function on linear regression:
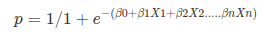
Properties of Logistic Regression:
- La variable dépendante de la régression logistique suit la distribution de Bernoulli.
- L’estimation se fait par maximum de vraisemblance.
- Pas de carré R, la fitness du modèle est calculée par Concordance, KS-Statistiques.
Régression linéaire Vs. Régression logistique
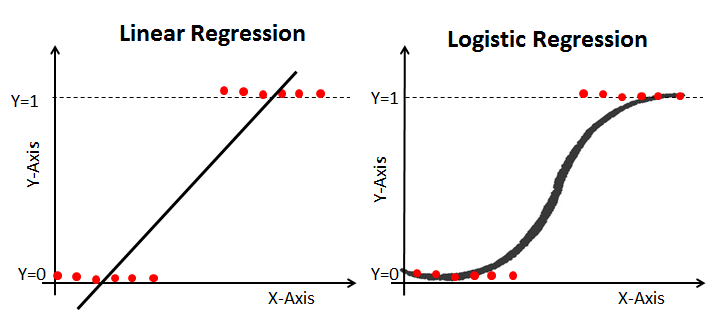
La régression linéaire vous donne une sortie continue, mais la régression logistique fournit une sortie constante. Un exemple de la production continue est le prix des maisons et le cours des actions. Un exemple de sortie discrète est de prédire si un patient a un cancer ou non, de prédire si le client va se désabonner. La régression linéaire est estimée à l’aide des Moindres Carrés ordinaires (LCO), tandis que la régression logistique est estimée à l’aide de l’approche de l’Estimation du Maximum de vraisemblance (ELM).
Estimation du maximum de vraisemblance Par rapport à la Méthode des moindres carrés
Le MLE est une méthode de maximisation de la « vraisemblance », tandis que l’OLS est une méthode d’approximation minimisant la distance. La maximisation de la fonction de vraisemblance détermine les paramètres les plus susceptibles de produire les données observées. D’un point de vue statistique, MLE définit la moyenne et la variance comme paramètres pour déterminer les valeurs paramétriques spécifiques pour un modèle donné. Cet ensemble de paramètres peut être utilisé pour prédire les données nécessaires dans une distribution normale.
Les estimations des moindres carrés ordinaires sont calculées en ajustant une droite de régression sur des points de données donnés qui a la somme minimale des écarts au carré (erreur des moindres carrés). Les deux sont utilisés pour estimer les paramètres d’un modèle de régression linéaire. MLE suppose une fonction de masse de probabilité conjointe, tandis que OLS ne nécessite aucune hypothèse stochastique pour minimiser la distance.
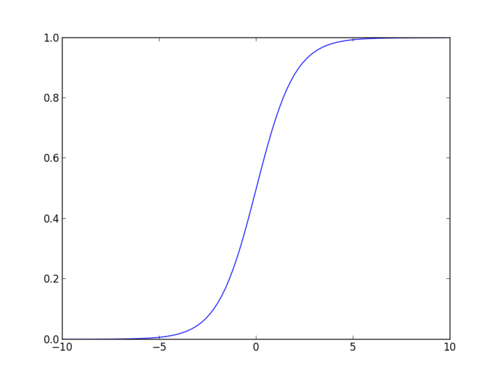
Fonction sigmoïde
La fonction sigmoïde, également appelée fonction logistique, donne une courbe en forme de « S » qui peut prendre n’importe quel nombre à valeur réelle et le mapper en une valeur comprise entre 0 et 1. Si la courbe passe à l’infini positif, y prédit deviendra 1, et si la courbe passe à l’infini négatif, y prédit deviendra 0. Si la sortie de la fonction sigmoïde est supérieure à 0,5, nous pouvons classer le résultat comme 1 ou OUI, et s’il est inférieur à 0.5, nous pouvons le classer comme 0 ou NON. La sortie ne peut pas par exemple: Si la sortie est de 0,75, nous pouvons dire en termes de probabilité: Il y a 75% de chances que le patient souffre d’un cancer.
Types de Régression Logistique
Types de Régression Logistique:
- Régression Logistique Binaire: La variable cible n’a que deux résultats possibles tels que Spam ou Non Spam, Cancer ou Pas de Cancer.
- Régression logistique multinomiale: La variable cible comporte trois catégories nominales ou plus telles que la prédiction du type de vin.
- Régression logistique ordinale: la variable cible a trois catégories ordinales ou plus telles que la notation du restaurant ou du produit de 1 à 5.
Construction de modèles dans Scikit-learn
Construisons le modèle de prédiction du diabète.
Ici, vous allez prédire le diabète en utilisant le Classificateur de régression logistique.
Chargeons d’abord l’ensemble de données de diabète indien Pima requis à l’aide de la fonction CSV de lecture des pandas. Vous pouvez télécharger les données à partir du lien suivant: https://www.kaggle.com/uciml/pima-indians-diabetes-database
Données de chargement
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
Sélection de la fonctionnalité
Ici, vous devez diviser les colonnes données en deux types de variables dépendantes (ou variable cible) et de variables indépendantes (ou variables de fonctionnalité).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variableFractionner les données
Pour comprendre les performances du modèle, diviser l’ensemble de données en un ensemble d’entraînement et un ensemble de test est une bonne stratégie.
Divisons l’ensemble de données en utilisant la fonction train_test_split(). Vous devez passer 3 caractéristiques de paramètres, target et test_set size. De plus, vous pouvez utiliser random_state pour sélectionner des enregistrements de manière aléatoire.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)Ici, l’ensemble de données est divisé en deux parties dans un rapport de 75:25. Cela signifie que 75% des données seront utilisées pour la formation des modèles et 25% pour les tests des modèles.
Développement et prédiction de modèles
Tout d’abord, importez le module de régression Logistique et créez un objet classificateur de régression logistique à l’aide de la fonction LogisticRegression().
Ensuite, ajustez votre modèle sur l’ensemble de trains à l’aide de fit() et effectuez une prédiction sur l’ensemble de tests à l’aide de predict().
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)Évaluation du modèle à l’aide d’une matrice de confusion
Une matrice de confusion est une table utilisée pour évaluer les performances d’un modèle de classification. Vous pouvez également visualiser les performances d’un algorithme. Le fondamental d’une matrice de confusion est le nombre de prédictions correctes et incorrectes résumées par classe.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])Ici, vous pouvez voir la matrice de confusion sous la forme de l’objet tableau. La dimension de cette matrice est 2 * 2 car ce modèle est une classification binaire. Vous avez deux classes 0 et 1. Les valeurs diagonales représentent des prédictions précises, tandis que les éléments non diagonaux sont des prédictions inexactes. Dans la sortie, 119 et 36 sont des prédictions réelles, et 26 et 11 sont des prédictions incorrectes.
Visualisation de la matrice de confusion à l’aide de Heatmap
Visualisons les résultats du modèle sous la forme d’une matrice de confusion à l’aide de matplotlib et seaborn.
Ici, vous visualiserez la matrice de confusion à l’aide d’une carte thermique.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
Mesures d’évaluation de la matrice de confusion
Évaluons le modèle à l’aide de mesures d’évaluation du modèle telles que la précision, la précision et le rappel.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226Eh bien, vous avez un taux de classification de 80%, considéré comme une bonne précision.
Précision: La précision consiste à être précis, c’est-à-dire à quel point votre modèle est précis. En d’autres termes, vous pouvez dire, quand un modèle fait une prédiction, à quelle fréquence elle est correcte. Dans votre cas de prédiction, lorsque votre modèle de régression logistique prédit que les patients vont souffrir de diabète, les patients ont 76% du temps.
Rappel: S’il y a des patients diabétiques dans l’ensemble de tests et que votre modèle de régression logistique peut l’identifier 58% du temps.
Courbe ROC
La courbe de caractéristique de fonctionnement du récepteur (ROC) est un graphique du taux positif réel par rapport au taux de faux positifs. Il montre le compromis entre sensibilité et spécificité.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
Le score AUC pour le cas est de 0,86. Le score AUC 1 représente un classificateur parfait et 0,5 représente un classificateur sans valeur.
Avantages
En raison de sa nature efficace et simple, ne nécessite pas de puissance de calcul élevée, facile à mettre en œuvre, facilement interprétable, largement utilisé par les analystes de données et les scientifiques. En outre, il ne nécessite pas de mise à l’échelle des fonctionnalités. La régression logistique fournit un score de probabilité pour les observations.
Inconvénients
La régression logistique n’est pas capable de gérer un grand nombre de caractéristiques /variables catégorielles. Il est vulnérable au surajustement. En outre, ne peut pas résoudre le problème non linéaire avec la régression logistique, c’est pourquoi il nécessite une transformation des caractéristiques non linéaires. La régression logistique ne fonctionnera pas bien avec des variables indépendantes qui ne sont pas corrélées à la variable cible et qui sont très similaires ou corrélées les unes aux autres.
Conclusion
Dans ce tutoriel, vous avez couvert beaucoup de détails sur la régression logistique. Vous avez appris ce qu’est la régression logistique, comment construire des modèles respectifs, comment visualiser les résultats et certaines des informations de base théoriques. En outre, vous avez couvert certains concepts de base tels que la fonction sigmoïde, la probabilité maximale, la matrice de confusion, la courbe ROC.
Avec un peu de chance, vous pouvez maintenant utiliser la technique de régression logistique pour analyser vos propres ensembles de données. Merci d’avoir lu ce tutoriel!
Si vous souhaitez en savoir plus sur la régression logistique, suivez le cours Fondements de l’analyse prédictive en Python de DataCamp (Partie 1).