Diamètre angulaire

Diamètre angulaire: l’angle sous-tendu par un objet

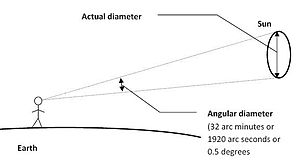
En astronomie, les tailles des objets célestes sont souvent données en fonction de leur diamètre angulaire vu de la Terre, plutôt que leurs tailles réelles. Comme ces diamètres angulaires sont généralement petits, il est courant de les présenter en secondes d’arc (« ). Une seconde d’arc vaut 1/3600e d’un degré (1°) et un radian vaut 180/π{\displaystyle\pi}

degrés. Ainsi, un radian est égal à 3 600 × 180/π{\displaystyle\pi}

arcsecondes, ce qui représente environ 206 265 arcsecondes (1 rad ≈ 206 264,806247″). Par conséquent, le diamètre angulaire d’un objet de diamètre physique d à une distance D, exprimé en secondes d’arc, est donné par : δ = 206, 265 (d/D) a r c s e c o n d s {\displaystyle\delta = 206,265 ~(d/D) ~\mathrm {arcsecondes}}

.

Ces objets ont un diamètre angulaire de 1″:

• un objet de diamètre 1 cm à une distance de 2,06 km
• un objet de diamètre 725,27 km à une distance de 1 unité astronomique (AU)
• un objet de diamètre 45 866 916 km à 1 année-lumière
• un objet de diamètre 1 UA (149 597 871 km) à une distance de 1 parsec (pc)

Ainsi, le diamètre angulaire de l’orbite terrestre autour du Soleil vu à une distance de 1 pc est de 2 « , car 1 UA est le rayon moyen de l’orbite terrestre.

Le diamètre angulaire du Soleil, à une distance d’une année-lumière, est de 0,03″, et celui de la Terre de 0,0003″. Le diamètre angulaire 0.03″ du Soleil donné ci-dessus est approximativement le même que celui d’un corps humain à une distance du diamètre de la Terre.

Ce tableau montre les tailles angulaires des corps célestes remarquables vus de la Terre :

Comparaison du diamètre angulaire du Soleil, de la Lune et des planètes. Pour obtenir une représentation fidèle des tailles, visualisez l’image à une distance de 103 fois la largeur de la « Lune: max. » cercle. Par exemple, si ce cercle a une largeur de 5 cm sur votre moniteur, visualisez-le à une distance de 5,15 m.

Cette photo compare les tailles apparentes de Jupiter et de ses quatre lunes galiléennes (Callisto à allongement maximal) avec le diamètre apparent de la pleine Lune lors de leur conjonction le 10 avril 2017.

Le tableau montre que le diamètre angulaire du Soleil, vu de la Terre, est d’environ 32′ (1920″ ou 0,53°), comme illustré ci-dessus.

Ainsi, le diamètre angulaire du Soleil est environ 250 000 fois celui de Sirius. (Sirius a deux fois le diamètre et sa distance est 500 000 fois plus; le Soleil est 1010 fois plus brillant, ce qui correspond à un rapport de diamètre angulaire de 105, donc Sirius est environ 6 fois plus brillant par unité d’angle solide.)

Le diamètre angulaire du Soleil est également environ 250 000 fois celui d’Alpha Centauri A (il a à peu près le même diamètre et la distance est 250 000 fois plus grande; le Soleil est 4×1010 fois plus brillant, ce qui correspond à un rapport de diamètre angulaire de 200 000, donc Alpha Centauri A est un peu plus brillant par unité d’angle solide).

Le diamètre angulaire du Soleil est à peu près le même que celui de la Lune. (Le diamètre du Soleil est 400 fois plus grand et sa distance aussi; le Soleil est 200 000 à 500 000 fois plus brillant que la pleine Lune (les chiffres varient), ce qui correspond à un rapport de diamètre angulaire de 450 à 700, donc un corps céleste d’un diamètre de 2,5 à 4 « et ayant la même luminosité par unité d’angle solide aurait la même luminosité que la pleine Lune.)

Même si Pluton est physiquement plus grande que Cérès, vue de la Terre (par exemple, à travers le télescope spatial Hubble), Cérès a une taille apparente beaucoup plus grande.

Les tailles angulaires mesurées en degrés sont utiles pour les grandes plaques de ciel. (Par exemple, les trois étoiles de la ceinture couvrent environ 4,5 ° de taille angulaire.) Cependant, des unités beaucoup plus fines sont nécessaires pour mesurer les tailles angulaires des galaxies, des nébuleuses ou d’autres objets du ciel nocturne.

Les degrés sont donc subdivisés comme suit:

• 360 degrés (°) dans un cercle complet
• 60 minutes d’arc (‘) dans un degré
• 60 secondes d’arc (« ) dans une minute d’arc

Pour mettre cela en perspective, la pleine Lune vue de la Terre est d’environ 1⁄2°, soit 30′ (ou 1800″). Le mouvement de la Lune dans le ciel peut être mesuré en taille angulaire: environ 15 ° toutes les heures, ou 15 « par seconde. Une ligne d’un mille de long peinte sur la face de la Lune apparaîtrait de la Terre d’environ 1 « de longueur.

En astronomie, il est généralement difficile de mesurer directement la distance à un objet, mais l’objet peut avoir une taille physique connue (peut-être similaire à un objet plus proche avec une distance connue) et un diamètre angulaire mesurable. Dans ce cas, la formule du diamètre angulaire peut être inversée pour donner la distance de diamètre angulaire aux objets distants comme

d ≡ 2 D tan ⁡(δ 2) {\displaystyle d\equiv 2D\tan\left({\frac{\delta}{2}}\right)}

.

Dans un espace non euclidien, tel que notre univers en expansion, la distance de diamètre angulaire n’est qu’une des nombreuses définitions de la distance, de sorte qu’il peut y avoir différentes « distances » au même objet. Voir Mesures de distance (cosmologie).

Objets non circulairesdit

De nombreux objets du ciel profond tels que les galaxies et les nébuleuses apparaissent non circulaires et reçoivent donc généralement deux mesures de diamètre : grand axe et petit axe. Par exemple, le Petit nuage de Magellan a un diamètre apparent visuel de 5° 20′ × 3° 5′.

Défaut d’éclairement

Le défaut d’éclairement est la largeur angulaire maximale de la partie non éclairée d’un corps céleste vue par un observateur donné. Par exemple, si un objet a une largeur d’arc de 40″ et est éclairé à 75%, le défaut d’éclairage est de 10″.