Distributions normales (Courbe en cloche): Définition, Problèmes de mots

Probabilité et statistiques > Distributions normales

Contenu:

1. Qu’est-ce qu’une distribution normale?
2. Le Modèle Normal Standard
3. Problèmes De Mots De Distribution Normale.
4. Distribution normale sur les exemples de TI 89
5. Articles connexes.

Qu’est-ce qu’une distribution normale ?

Une distribution normale.

Une distribution normale, parfois appelée courbe en cloche, est une distribution qui se produit naturellement dans de nombreuses situations. Par exemple, la courbe en cloche est visible dans des tests tels que SAT et GRE. La majeure partie des étudiants obtiendront la note moyenne (C), tandis qu’un plus petit nombre d’étudiants obtiendront la note B ou D. Un pourcentage encore plus faible d’étudiants obtiendra la note F ou A. Cela crée une distribution qui ressemble à une cloche (d’où le surnom). La courbe en cloche est symétrique. La moitié des données tombera à gauche de la moyenne; la moitié tombera à droite.
De nombreux groupes suivent ce type de modèle. C’est pourquoi il est largement utilisé dans les affaires, les statistiques et dans les organismes gouvernementaux comme la FDA:

• Hauteurs de personnes.
• Erreurs de mesure.
• Pression artérielle.
• Points sur un test.
• Scores de QI.
• Salaires.

La règle empirique vous indique quel pourcentage de vos données se situe dans un certain nombre d’écarts types par rapport à la moyenne:
•68% des données se situent dans un écart type de la moyenne.
• 95 % des données se situent à deux écarts types de la moyenne.
• 99,7% des données se situent à moins de trois écarts types de la moyenne.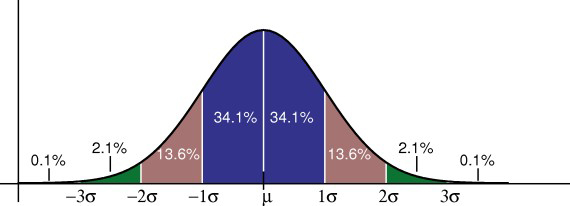

L’écart type contrôle la propagation de la distribution. Un écart-type plus petit indique que les données sont étroitement groupées autour de la moyenne; la distribution normale sera plus grande. Un écart-type plus important indique que les données sont réparties autour de la moyenne; la distribution normale sera plus plate et plus large.

Propriétés d’une distribution normale

• La moyenne, le mode et la médiane sont tous égaux.
• La courbe est symétrique au centre (c’est-à-dire autour de la moyenne, μ).
• Exactement la moitié des valeurs sont à gauche du centre et exactement la moitié des valeurs sont à droite.
• La surface totale sous la courbe est de 1.

Le Modèle Normal Standard
Un modèle normal standard est une distribution normale avec une moyenne de 0 et un écart type de 1.

Modèle normal standard: Distribution des données

Une façon de déterminer comment les données sont distribuées est de les tracer dans un graphique. Si les données sont réparties uniformément, vous pouvez créer une courbe en cloche. Une courbe en cloche a un faible pourcentage des points sur les deux queues et le pourcentage le plus élevé sur la partie interne de la courbe. Dans le modèle normal standard, environ 5% de vos données tomberaient dans les « queues” (de couleur orange plus sombre dans l’image ci-dessous) et 90% se situeraient entre les deux. Par exemple, pour les résultats aux tests des élèves, la distribution normale indiquerait 2,5% des élèves obtenant des scores très faibles et 2.5% obtiennent des scores très élevés. Le reste sera au milieu; ni trop haut ni trop bas. La forme de la distribution normale standard ressemble à ceci :

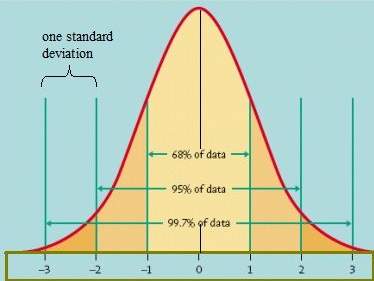
Modèle normal standard. Crédit d’image: Université de Virginie.

Applications pratiques du Modèle Normal standard

La distribution normale standard pourrait vous aider à déterminer dans quel sujet vous obtenez de bonnes notes et dans quels sujets vous devez faire plus d’efforts en raison de faibles pourcentages de notation. Une fois que vous obtenez un score dans un sujet qui est plus élevé que votre score dans un autre sujet, vous pourriez penser que vous êtes meilleur dans le sujet où vous avez obtenu le score le plus élevé. Ce n’est pas toujours vrai.

Vous ne pouvez dire que vous êtes meilleur dans un sujet particulier que si vous obtenez un score avec un certain nombre d’écarts types au-dessus de la moyenne. L’écart type vous indique à quel point vos données sont regroupées autour de la moyenne ; Il vous permet de comparer différentes distributions qui ont différents types de données, y compris différentes moyennes.

Par exemple, si vous obtenez un score de 90 en mathématiques et de 95 en anglais, vous pourriez penser que vous êtes meilleur en anglais qu’en mathématiques. Cependant, en mathématiques, votre score est de 2 écarts types au-dessus de la moyenne. En anglais, ce n’est qu’un écart type au-dessus de la moyenne. Il vous indique qu’en mathématiques, votre score est beaucoup plus élevé que la plupart des étudiants (votre score tombe dans la queue).
Sur la base de ces données, vous avez obtenu de meilleurs résultats en mathématiques qu’en anglais!

Questions de probabilité utilisant le Modèle standard

Les questions sur la probabilité de distribution normale standard peuvent sembler alarmantes, mais la clé pour les résoudre consiste à comprendre ce que représente l’aire sous une courbe normale standard. La surface totale sous une courbe de distribution normale standard est de 100% (c’est-à-dire « 1” en décimal). Par exemple, la moitié gauche de la courbe est de 50%, ou.5. Donc, la probabilité qu’une variable aléatoire apparaisse dans la moitié gauche de la courbe est.5.

Bien sûr, tous les problèmes ne sont pas aussi simples, c’est pourquoi il existe une table en z. Tout ce qu’une table z fait est de mesurer ces probabilités (c’est-à-dire 50%) et de les placer en écarts types par rapport à la moyenne. La moyenne est au centre de la distribution normale standard et une probabilité de 50% est égale à zéro écart-type.

Distribution normale standard: Comment trouver la probabilité (Étapes)

Étape 1: Dessinez une courbe en cloche et une nuance dans la zone demandée dans la question. L’exemple ci-dessous montre z > -0,8. Cela signifie que vous recherchez la probabilité que z soit supérieur à -0,8, vous devez donc tracer une ligne verticale à -0.8 écarts types par rapport à la moyenne et ombrage tout ce qui est supérieur à ce nombre.

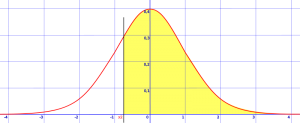
la zone ombrée est z >-0,8

Étape 2: Visitez l’indice de la zone de probabilité normale et trouvez une image qui ressemble à votre graphique. Suivez les instructions de cette page pour trouver la valeur z du graphique. La valeur z est la probabilité.

Astuce: L’étape 1 est techniquement facultative, mais c’est toujours une bonne idée d’esquisser un graphique lorsque vous essayez de répondre à des problèmes de mots de probabilité. C’est parce que la plupart des erreurs se produisent non pas parce que vous ne pouvez pas faire le calcul ou lire un tableau z, mais parce que vous soustrayez un score z au lieu d’ajouter (c’est-à-dire que vous imaginez la probabilité sous la courbe dans la mauvaise direction. Un croquis vous aide à cimenter dans votre tête exactement ce que vous recherchez.

Si vous rencontrez toujours des problèmes, consultez les tuteurs à Chegg.com . Vos 30 premières minutes avec un tuteur en direct sont gratuites!

Problèmes de mots de distribution normaux

Cette vidéo montre un exemple de problème de mots de distribution normaux. Pour plus d’exemples, lisez ci-dessous:

Lorsque vous abordez la distribution normale dans une classe de statistiques, vous essayez de trouver l’aire sous la courbe. La surface totale est de 100% (en décimal, c’est 1). Les problèmes de distribution normaux sont de six types de base. Comment savez-vous qu’un problème de mot implique une distribution normale? Recherchez la phrase clé « supposons que la variable est normalement distribuée » ou « supposons que la variable est à peu près normale.”Pour résoudre un problème de mot, vous devez déterminer le type que vous avez.

1. « Entre”: Contient l’expression « entre” et comprend une limite supérieure et une limite inférieure (c.-à-d. « trouvez le nombre de maisons dont le prix se situe entre 50 000 $ et 200 000 $”).
2. « Plus que” ou « Au-dessus »: contient la phrase ”plus que » ou ”au-dessus ».
3. « Inférieur à”.
4. Exemple de Coupure Inférieure (vidéo)
5. Exemple de coupure Supérieure (vidéo)
6. Exemple de Pourcentage moyen (vidéo)

« Entre”

Ce mode d’emploi couvre la résolution de problèmes contenant l’expression « entre” et inclut une limite supérieure et inférieure (c’est-à-dire « trouvez le nombre de maisons dont le prix se situe entre 50 000 $ et 200 000 houses”. Notez que cela est différent de trouver le « pourcentage moyen” de quelque chose.

Problèmes de mots avec une distribution normale: ”Entre »: Étapes

Étape 1: Identifiez les parties du problème de mots. Le mot problème identifiera :

1. La moyenne (moyenne ou μ).
2. Écart type (σ).
3. Nombre sélectionné (c’est-à-dire « choisissez un au hasard” ou « sélectionnez dix au hasard”).
4. X: les nombres associés à « entre » (c’est-à-dire ”entre 5 000 $ et 10 000 $ » auraient X comme 5 000 et comme 10 000 $).

De plus, vous recevrez SOIT:

1. Taille de l’échantillon (soit 400 maisons, 33 personnes, 99 usines, 378 plombiers, etc.). OU
2. On pourrait vous demander une probabilité (auquel cas la taille de votre échantillon sera probablement tout le monde, c’est-à-dire « Plombiers compagnons” ou « Pilotes de première année. »

Étape 2: Dessinez un graphique. Placez la moyenne que vous avez identifiée à l’étape 1 au centre. Mettez le nombre associé à « entre” sur le graphique (devinez où les nombres tomberaient – cela n’a pas besoin d’être exact). Par exemple, si votre moyenne était de 100 $ et qu’on vous demandait « salaire horaire entre 75 $ et 125 $”), votre graphique ressemblera à ceci:

Étape 3: Calculez les scores z . Branchez la première valeur X (dans mon graphique ci-dessus, c’est 75) dans la formule de la valeur z et résolvez. Le μ (la moyenne), est 100 à partir du graphique de l’échantillon. Vous pouvez obtenir ces chiffres (y compris σ, l’écart type) à partir de vos réponses à l’étape 1 :

*Remarque: si la formule vous confond, toute cette formule vous demande de faire est:
1. soustrayez la moyenne de X
2. divisez par l’écart type.

Étape 4: Répétez l’étape 3 pour le deuxième X.

Étape 5: Prenez les chiffres des étapes 3 et 4 et utilisez-les pour trouver la zone dans la table z.

Si on vous a demandé de trouver une probabilité dans votre question, passez à l’étape 6a. Si on vous a demandé de trouver un nombre à partir d’une taille d’échantillon donnée spécifique, passez à l’étape 6b.

Étape 6a:

Convertissez la réponse de l’étape 5 en pourcentage.

Par exemple, 0,1293 est 12,93%.

C’est tout – sautez l’étape 6b!

Étape 6b

Multipliez la taille de l’échantillon (trouvée à l’étape 1) par la valeur z trouvée à l’étape 4. Par exemple, 0,300 * 100 = 30.

C’est tout!

« Plus que” ou « Au-dessus”

Ce mode d’emploi couvre la résolution de problèmes de distribution normaux qui contiennent l’expression « plus que” (ou une expression comme « au-dessus”).

Étape 1: Décomposez le problème de mot en plusieurs parties. Trouver:

1. La moyenne (moyenne ou μ)
2. Écart type (σ)
3. Un nombre (par exemple, « choisissez cinquante au hasard” ou « sélectionnez 90 au hasard”)
4. X: le nombre associé à l’instruction « moins de”. Par exemple, si on vous demandait de trouver « moins de 9 999 $”, alors X vaut 9 999.

Étape 2: Trouvez l’échantillon du problème. Vous aurez soit une taille spécifique (comme « 1000 téléviseurs”), soit un échantillon général (« Chaque télévision”).

Dessinez une image si le problème avec la moyenne et la zone que vous recherchez. Par exemple, si la moyenne est de 15 $ et qu’on vous a demandé de trouver les dîners qui coûtent plus de 10 $, votre graphique pourrait ressembler à ceci:

Étape 3: Calculez le score z (branchez vos valeurs dans le z formule de valeur et résoudre). Utilisez vos réponses de l’étape 1 :

Fondamentalement, tout ce que vous faites avec la formule est de soustraire la moyenne de X, puis de diviser cette réponse par l’écart type.

Étape 4: Recherchez la zone à l’aide du score z de l’étape 3. Utilisez la table en z. Vous ne savez pas comment lire une table en z? Voir la vidéo sur la page z-table.

Étape 6: Passez à l’étape 6a pour trouver une probabilité OU passez à l’étape 6b pour calculer un certain nombre ou montant.

Étape 6a
Transformez la réponse de l’étape 5 en pourcentage.

Par exemple, 0,1293 est 12,93%.

Sauter l’étape 6b : vous avez terminé!

Étape 6b
Multipliez la taille de l’échantillon de l’étape 1 par le score z de l’étape 4. Par exemple, 0,500 * 100 = 50.

Vous avez terminé!

Inférieur à

Ce mode d’emploi couvre la résolution de problèmes de mots de distribution normaux qui ont la phrase « moins de” (ou une phrase similaire telle que « moins de”).

Problèmes de mots de distribution normale inférieurs à: Étapes

Étape 1: Décomposez le problème de mots en parties:

1. La moyenne (moyenne ou μ)
2. Écart type (σ)
3. Nombre sélectionné (c’est-à-dire « choisissez un au hasard » ou « sélectionnez dix au hasard »)
4. X: le nombre qui va avec ”moins de » (c’est-à-dire ”moins de 99 000 $ » indiquerait X comme 99 000)

De plus, vous aurez SOIT:

1. Une taille d’échantillon spécifique. Par exemple, 500 bateaux, 250 sandwichs, 100 téléviseurs, etc.
2. Tout le monde dans l’échantillon (il vous sera demandé de trouver une probabilité). Par exemple, « étudiants en première année de médecine », « Patients atteints de cancer” ou « Pilotes de ligne. »

Étape 2: Dessinez une image pour vous aider à visualiser le problème. Le graphique suivant montre une moyenne de 15 et une zone « inférieure à 4 »):

Étape 3: Trouvez la valeur z en branchant les valeurs données dans la formule. Le « X » dans notre graphique d’échantillon est 4 et le μ (ou moyen) est 15. Vous pouvez obtenir ces chiffres (y compris σ, l’écart-type) à partir de vos réponses à l’étape 1, où vous avez identifié les parties du problème:

Tout ce que vous avez à faire pour résoudre la formule est:

1. Soustrayez la moyenne de X.
2. Divisez par l’écart type.

Étape 4: Prenez le numéro de l’étape 3, puis utilisez la table en z pour trouver la zone.

Étape 5: Pour trouver une probabilité, passez à l’étape 6a. Pour trouver un nombre à partir d’une taille d’échantillon donnée spécifique, passez à l’étape 6b.

Étape 6a

Changez le nombre de l’étape 5 en pourcentage.

Par exemple, 0,1293 est 12,93%.

C’est tout!

Étape 6b

Multipliez la taille de l’échantillon (trouvée à l’étape 1) par la valeur z trouvée à l’étape 4. Par exemple, 0,300 * 100 = 30.

C’est tout!

Coupure inférieure

Parfois, sur un problème de mot de distribution normal, il vous sera demandé de trouver une ”limite inférieure d’un pourcentage supérieur » de quelque chose (c’est-à-dire ”trouver le point de coupure pour réussir un certain examen où les 40% supérieurs des candidats aux tests réussissent »). Un point de coupure inférieur est le point où les scores tomberont en dessous de ce point. Par exemple, vous voudrez peut-être trouver le point de coupure pour les 10% les plus bas des candidats.

Consultez notre chaîne YouTube pour plus de problèmes.

Distribution normale TI 89 Exemples

Dans les statistiques élémentaires, vous serez souvent confronté à une question qui vous demande les points de coupure pour un certain pourcentage de la distribution normale, comme les 90% supérieurs ou les 10% supérieurs. Bien que l’élaboration de ces types de problèmes à la main soit fastidieuse, la calculatrice graphique TI-89 permet de trouver des points de coupure pour un pourcentage supérieur avec la fonction normale inverse. Ce que vous faites réellement, c’est rechercher les points de coupure pour un certain percentile: par exemple, si vous avez une liste de notes et que vous voulez savoir quel score est au 99e centile, vous pouvez utiliser la fonction normale inverse pour trouver ce point de seuil de pourcentage.

Trouver Des Points de coupure Pour un Pourcentage Supérieur

Exemple de problème: Les étudiants d’un certain collège mesurent en moyenne 5 pieds 8 pouces (68 pouces). Les hauteurs sont normalement réparties, avec un écart type de 2,5 pouces. Quelle est la valeur qui sépare le 1% supérieur des hauteurs du reste de la population?

Étape 1: Appuyez sur APPLICATIONS et utilisez les touches de défilement pour mettre en surbrillance l’éditeur de statistiques / liste.

Étape 2: Appuyez sur F5 2 1 (cela vous amène à l’écran Normal Inverse).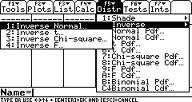

Étape 3: Entrez 0,99 dans la zone Zone.

Étape 4: Entrez 68 dans la case μ.

Étape 5: Entrez 2,5 dans la case σ.Étape 6 : Appuyez sur ENTRÉE.

Étape 7: Lisez les résultats: Inverse = 73,8159 signifie que la hauteur de coupure pour le 99e centile est de 73,8159 pouces.

C’est tout!

Exemple de Proportion de probabilité (fonction NormalCDF)

Exemple de question: Un groupe d’étudiants avec des salaires normalement distribués gagne en moyenne 6 800 with avec un écart-type de 2 500 $. Quelle proportion d’étudiants gagnent entre 6 500 $ et 7 300 $?

Étape 1: Appuyez sur APPLICATIONS. Faites défiler jusqu’à l’éditeur de statistiques / liste et appuyez sur ENTRÉE.

Étape 2: Appuyez sur F5 4.

Étape 3: Entrez 6500 dans la zone valeur inférieure.

Étape 4: Entrez 7300 dans la zone de valeur supérieure.

Étape 5: Entrez 6800 dans la case μ.

Étape 6: Entrez 2500 dans la case σ. Appuyez sur ENTRÉE.

Étape 7: Lisez la réponse. CDF=.127018. En d’autres termes, .013, soit 13% des étudiants gagnent entre 6 500 $ et 7 300 $.

TI-89 Représentant une courbe de distribution normale

La TI-89 peut non seulement calculer des scores z et renvoyer des valeurs pour des distributions normales, mais elle peut également représenter la courbe de distribution normale. La représentation graphique d’une distribution normale peut vous aider à voir ce que vous êtes censé rechercher et vous donne un outil de plus pour résoudre les problèmes de distribution normale. Le TI-89 peut représenter une courbe de distribution normale avec une zone ombrée pour n’importe quelle valeur. Par exemple, vous pouvez créer un graphique qui est: inférieur à un certain nombre, supérieur à un certain nombre, ou entre un certain ensemble de nombres.

Exemple de problème : Tracez une courbe de distribution normale pour les salaires des étudiants au cours d’un semestre typique. Les salaires des étudiants ont une moyenne de 6 800 $ et un écart-type de 2 500 $. Ombrez la zone du graphique qui correspond aux salaires entre 7 300 $ et 9 000 $.

Étape 1: Appuyez sur APPLICATIONS et sélectionnez l’éditeur de statistiques / liste.

Étape 2: Appuyez sur F2 3 et F2 4.

Étape 3: Appuyez sur F5) 1.

Étape 4: Faites défiler vers le bas et entrez 7300 dans la zone valeur inférieure.

Étape 5: Faites défiler vers le bas et entrez 9000 dans la zone de valeur supérieure.

Étape 6: Faites défiler vers le bas et entrez 6800 dans la boîte μ.

Étape 7: Faites défiler vers le bas et entrez 2500 dans la zone σ.

Étape 8: Faites défiler vers le bas. Tournez l’échelle automatique sur « oui » en appuyant sur la touche de défilement droite, puis sur la touche de défilement vers le bas pour sélectionner oui. Appuyez sur ENTRÉE.

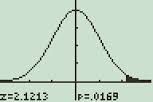
Un graphique de distribution normale affiché sur la calculatrice TI-89.

C’est tout!

Astuce: Si vous souhaitez entrer ∞ (infinity) comme l’une de vos valeurs inférieures ou supérieures, appuyez sur la touche losange, puis sur Catalogue.

Beyer, W. H. Tableaux mathématiques standard CRC, 28e éd. Boca Raton, FL : CRC Press, p. 533-534, 1987.
Feller, W. Une Introduction à la Théorie des Probabilités et à ses Applications, Vol. 1, 3e éd. Il est le père de la famille.
Kenney, J. F. et Keeping, E. S. Mathématiques de la statistique, Pt. 2, 2e éd. Il s’agit de la première édition de la série.
Kraitchik, M. « La courbe d’erreur. »§6.4 dans Récréations mathématiques. Il s’agit de la première édition de la série.
Patel, J. K. et Read, C. B. Manuel de la Distribution normale. 1982 : Dekker, New York.

1. Quelle est la règle 68-95-99.7?
2. Transformation de Box Cox
3. Transformation de Box Muller
4. Modèles de Mélange Gaussien.
5. Qu’est-ce qu’un diagramme de probabilité normal ?
6. Comment calculer un Score Z dans les statistiques
7. Trouvez la zone à droite d’un score z.
8. Utiliser l’approximation normale pour résoudre un Problème binomial
9. Quel est le facteur de correction de continuité ?
10. Aire Sous un Indice de Courbe de Distribution Normale
11. Théorème de Limite Centrale.
12. La Distribution Normale De Biais.
13. Courbe Normale à Deux queues.
14. La fonction Q.

——————————————————————————

Besoin d’aide pour une question de devoirs ou de test? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites!