Parcimonie maximale sur les réseaux phylogénétiques

Définition des réseaux phylogénétiques

Nous suivons la définition des réseaux phylogénétiques telle que donnée dans, Définition 4, page 16]. Pour toutes les autres définitions théoriques de graphes qui ne sont pas données ici, nous suivons. Un réseau phylogénétique enraciné, simplement appelé ici un réseau phylogénétique, est défini comme un graphe acyclique dirigé enraciné (DAG), dont la racine a un degré indé 0 et les feuilles un degré extérieur 0. Les sommets dont l’indegree est supérieur à 1 sont appelés sommets réticulés et les arêtes avec des sommets réticulés comme sommets de tête sont appelées arêtes réticulées. Toutes les autres arêtes sont appelées arêtes d’arbre. La définition donnée dans prend en charge la retenue dite de « cohérence temporelle », à savoir que les bords des arbres se déroulent dans un temps positif et que les sommets réticulés ont des parents qui ne peuvent que « coexister dans le temps ». Par conséquent, nous rappelons la définition formelle des réseaux phylogénétiques telle qu’elle est donnée dans.

Étant donné tout graphe dirigé, on dit que deux sommets u et v ne peuvent pas coexister dans le temps s’il existe une séquence P =(p1, p2,…, p k) de chemins dans N tels que :

1. p i est un chemin dirigé qui contient au moins une arête d’arbre, pour chaque 1 ≤ i ≤ k,

2. u est la queue de p 1, et v est la tête de p k, et

3. pour chaque 1 ≤ i ≤ k-1, il existe un sommet de réseau dont les deux parents sont la tête p i et la queue de p i +1.

Un réseau phylogénétique N est un DAG enraciné obéissant aux contraintes suivantes:

1. Chaque sommet a indegree et outdegree définis par l’une des quatre combinaisons (0, 2), (1, 0), (1, 2), or(2, 1) – correspondant respectivement aux racines, aux feuilles, aux sommets internes des arbres et aux sommets réticulés. Tous les sommets autres que les sommets réticulés sont appelés sommets arborescents.

2. Si deux sommets u et v ne peuvent pas coexister dans le temps, il n’existe pas de sommet de réseau w avec des arêtes (u, w) et (v, w).

3. Compte tenu de n’importe quel bord du réseau, au moins un de ses points de terminaison doit être un sommet d’arbre.

Une autre composante de cette définition est que pour n’importe quelle arête du réseau phylogénétique, au moins un de ses points finaux (soit la tête ou la queue) est un sommet d’arbre. Ici, nous utiliserons cette définition. Dans la mesure du possible, nous indiquons si les conditions de la définition sont nécessaires.

Les réseaux phylogénétiques peuvent être naïvement considérés comme un réseau qui contient comme sous-graphes, les arbres qui expliquent les histoires évolutives des différents segments des séquences de bornes d’entrée. Étant donné un réseau phylogénétique, la suppression d’une de chaque arête incidente à un sommet réticulé ne garantit pas un arbre phylogénétique résultant avec le même ensemble de feuilles que celui du réseau. C’est une propriété indésirable, surtout si le critère de parcimonie est défini en trouvant un arbre phylogénétique à l’intérieur du réseau qui est le plus parcimonieux pour le site donné, tel que défini dans. Afin d’éviter ce problème, il est nécessaire de supposer qu’aucun sommet interne n’a deux enfants réticulés. Nous appelons cette classe de réseaux phylogénétiques un réseau phylogénétique sans réticulations sœurs. Voir la figure 1 pour quelques exemples de réseaux phylogénétiques.

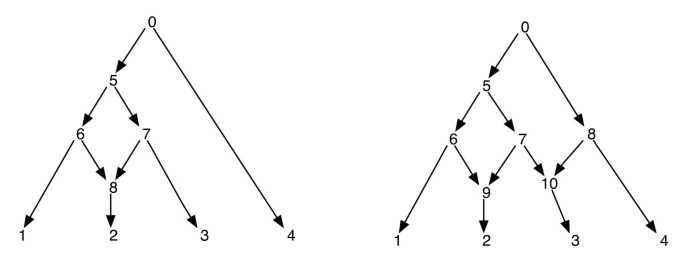
Réseaux phylogénétiques. La figure montre deux réseaux phylogénétiques; celui de gauche n’a qu’un seul sommet réticulé et celui de droite a deux sommets réticulés qui sont sœurs l’une de l’autre. Notez que la suppression des arêtes (7, 9) et (7, 10) du réseau de droite n’entraîne pas un arbre où le sommet 7 est une feuille. Cela montre que la suppression d’une arête entrante par sommet réticulé ne produit pas nécessairement un arbre avec le même jeu de feuilles que le réseau. Le post-ordre et le pré-ordre des sommets du réseau sur la gauche sont 1, 2, 8, 6, 3, 7, 5, 4, 0 et 0, 5, 6, 1, 8, 2, 7, 3, 4 respectivement et pour le réseau à droite, ils sont 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 et 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respectivement.

Avant de passer à la définition des problèmes de parcimonie, voici une observation utile. Pour un réseau phylogénétique N sans réticulations sœurs, et ayant r sommets réticulés et avec l’ensemble de feuilles X, nous désignons T(N) comme l’ensemble de tous les arbres contenus dans N. Chacun de ces arbres est obtenu en suivant deux étapes: (1) pour chaque sommet réticulé, retirez l’une des arêtes entrantes, puis (2) pour chaque sommet v d’indegrés et d’outdegrés 1, dont le parent est u et l’enfant est w, contractez les arêtes (u, v) et (v, w) en une seule arête (u, w) . La condition que chaque arête de N ait un sommet d’arbre en tant que point final et que chaque sommet d’arbre ait au moins un sommet d’arbre en tant qu’enfant garantit que l’ensemble des feuilles de l’arbre résultant est le même que celui du réseau. Par conséquent, l’ensemble T(N) contient exactement 2 arbres phylogénétiques dont l’ensemble des feuilles est exactement X.

Parcimonie maximale

Nous renvoyons les lecteurs à une description générale de l’idée de parcimonie et à la discussion de divers algorithmes de parcimonie. Il a été souligné que la méthode de parcimonie pour les arbres peut être étendue aux réseaux phylogénétiques. Dans une série d’articles, un tel critère de parcimonie est défini en trouvant un arbre dans le réseau qui a le meilleur score de parcimonie, et des algorithmes efficaces pour optimiser ce critère sur un réseau phylogénétique donné ont été conçus. Bien qu’il soit démontré que ces algorithmes fonctionnent bien dans la pratique, ils ne peuvent fonctionner correctement que pour les réseaux phylogénétiques sans réticulations sœurs, car il est simple de rechercher un arbre optimal dans ces classes restreintes de réseaux. Dans cette section, nous présentons une version alternative du problème de parcimonie et dans les sections suivantes, nous fournissons des solutions heuristiques pour optimiser le score sur n’importe quel réseau phylogénétique.

Let = {1, 2,…, n} désignent l’ensemble des étiquettes foliaires d’un réseau phylogénétique donné N. Une fonction λ : → {0, 1,…| /Σ/-1} est appelée une fonction d’affectation d’état sur l’alphabet Σ (un ensemble non vide) pour N. On dit qu’une fonction λ^: V(N ) → { 0 , 1 , … , | Σ/-1} est une extension de λ sur N si elle est d’accord avec λ sur les feuilles de N. Pour un sommet v dans N, on appelle λ^(v) une affectation de λ^ sur v. Un réseau entièrement attribué est un réseau dans lequel tous les sommets ont des étiquettes de {0, 1,…, |Σ| – 1}. Soit C une matrice de coûts dont ij entry entrée c ij est le coût de transformation de l’état i à l’état j le long d’une arête quelconque de N. Si e =(u, v) est une arête de N, où u est le parent de v, on désigne w e(λ) ^ = c i j, où i = λ ^(u) et j = λ ^(v). Pour un graphe G, on laisse E(G) désigner l’ensemble des arêtes de G. Alors le problème de parcimonie est défini comme suit.

Entrée: Un réseau phylogénétique N avec des étiquettes de feuilles et une fonction d’affectation d’état λ sur l’alphabet Σ pour N.

Critère de parcimonie : Pour une extension λ^ de λ, soit

et

Sortie: Étant donné P ∈{P1, P2}, trouvez λ^ qui minimise P(λ^).

Nous notons que P 1(λ^) est introduit dans et P 2 (λ^) est la définition que nous utiliserons dans cet article. Une approche plus générale consiste à minimiser Q(λ^) = ∑ e ∈ E(N) d e(w e(λ^)), où d e est une fonction de poids non négative sur les bords de N. Pour les besoins de cet article, nous nous limitons à P = P2, bien que la première de nos approches, la solution de programmation dynamique vaut également pour P = Q.

Algorithmes de parcimonie sur les réseaux

Traversant un réseau phylogénétique

Dans un réseau, sommet la traversée fait référence au processus de visite de chaque sommet, exactement une fois, de manière systématique. Ces traversées sont classées selon l’ordre dans lequel les sommets sont visités. Nous avons besoin de deux types de traversées de sommets de réseau pour décrire nos algorithmes. Ceux-ci sont bien connus pour les arbres phylogénétiques, et nous les présentons ici pour les réseaux phylogénétiques. Les algorithmes pour les traversées données ci-dessous partent de n’importe quel sommet v donné du réseau. Dans cet article, nous effectuerons toujours les traversées à partir du sommet racine du réseau.

Traversée précommandée d’un réseau phylogénétique à partir d’un sommet v

1. Visitez le sommet v.

2. Effectuez récursivement une traversée précommandée à partir de chaque enfant qui n’a pas encore été visité.

Traversée post-ordre d’un réseau phylogénétique à partir d’un sommet v

1. Effectuer récursivement une traversée post-ordre à partir de chaque enfant qui n’a pas encore été visité.

2. Visitez le sommet v.

Puisqu’un réseau phylogénétique est un DAG, de telles traversées visiteront tous les sommets du réseau exactement une fois. (Reportez-vous à pour plus de détails sur l’existence de telles traversées sur les DAG). Pour les besoins de cet article, nous supposons que les sommets d’un réseau sont étiquetés de manière unique par des entiers. Notez que les feuilles sont déjà étiquetées de l’ensemble ; et nous utilisons donc d’autres entiers pour d’autres sommets. Chaque fois que les sommets enfants de v sont extraits, ils sont également disposés dans l’ordre croissant de leurs étiquetages entiers et les traversées d’ordre pré et post sont effectuées dans cet ordre. Ceci assurera ce qui suit : si les sommets v et v’ sont tels qu’il n’y a pas de chemin dirigé entre eux, alors le sommet v est traversé avant le sommet v’ dans le pré-ordre si et seulement si le sommet v est traversé avant le sommet v’ dans le post-ordre. Voir la figure 1 pour quelques exemples. Avec cette propriété, nous remarquons que les traversées pré- et post-ordre à partir de la racine d’un réseau phylogénétique tracent chacune le même arbre couvrant, que nous appelons ici l’arbre traversant.

Solution de programmation dynamique

La programmation dynamique est utilisée pour fournir des solutions efficaces pour trouver le score de parcimonie exact lorsque le réseau est un arbre phylogénétique. Dans cette section, nous montrons que la même approche peut être généralisée aux réseaux phylogénétiques. L’algorithme de Sankoff sur un arbre parcourt les sommets de l’arbre via une post-commande tout en calculant les coûts minimaux de chaque état à chaque sommet des feuilles à la racine, puis choisit les meilleures affectations sur chaque sommet en revenant de la racine aux feuilles en parcourant les sommets de l’arbre via une pré-commande. Les deux phases sont présentées pour les réseaux dans les algorithmes 1 et 2 respectivement. Nous les décrivons brièvement ci-dessous. On peut noter que si le réseau est un arbre, alors nos algorithmes correspondent aux phases de pré-commande et de post-commande de la méthode de Sankoff pour les arbres.

Étant donné un réseau phylogénétique N, avec des sommets de feuilles étiquetés et avec une fonction d’affectation d’état λ sur l’alphabet Σ, assigner à chaque sommet v ∈ V une quantité S v(i) pour chaque i ∈ Σ. Dans les arbres phylogénétiques, S v(i) désigne la somme minimale des coûts de tous les événements du sommet v à toutes les feuilles accessibles à partir de v, étant donné que v est affecté à l’état i et que tous les sommets descendants de v sont chacun affectés d’un état. Dans les réseaux, il n’existe pas de moyen simple de calculer une telle quantité. Au lieu de cela, nous permettons à S v(i) d’être une borne inférieure du score exact ci-dessus et il est calculé pendant la phase de traversée post-ordre.

Phase de traversée post-ordre : Si v est une feuille de N, alors S v(i) est affecté à 0 si l’état observé est l’état i, et infini sinon. Maintenant, tout ce dont nous avons besoin est une relation de récursivité pour calculer S v(i) pour le reste des sommets. Pour chaque enfant w de v, on dit que w satisfait la condition de traversée post-ordre par rapport à v, ou simplement la condition de traversée par rapport à v compte tenu de l’observation au début de cette section, si la tenue suivante:

1. (i)

   Le sommet w est un sommet réticulé et

2. (ii)

   si v’ est le parent de w autre que v, alors le sommet v doit être traversé avant v’ dans la traversée post-ordre de N.

Nous définissons maintenant récursivement pour chaque arête (v, w),

Pour un arbre phylogénétique, s(v, w)(i) suppose toujours la première de ces grandeurs, et il donne ainsi la somme des coûts de substitution le long des arêtes de l’arbre qui se trouvent en dessous du sommet v, à condition que le sommet v se voit attribuer l’état i. Pour les réseaux phylogénétiques, afin de tenir compte des coûts de substitution le long des arêtes qui se trouvent en dessous d’un sommet réticulé w une seule fois où le sommet v se voit attribuer l’état i, nous laissons le « parent » v de w dans le l’arbre transversal représente tous les coûts de substitution le long de toutes les arêtes situées en dessous de v. D’autre part, si v n’est pas un parent de w dans l’arbre de traversée, s(v, w)(i) désigne simplement le coût de substitution de l’état i au sommet v à un autre état à w le moins coûteux.

Nous définissons ensuite

où la somme s’exécute pour tous les sommets enfants w de v. Comme mentionné précédemment, dans les arbres phylogénétiques, S v(i) désigne la somme minimale possible des coûts de substitution le long de toutes les arêtes du sommet v à toutes les feuilles accessibles depuis v, étant donné que v est affecté à l’état i et que tous les sommets accessibles depuis v sont chacun affectés d’un état.

Dans les réseaux phylogénétiques, lors du calcul de s(v, w)(i) où w est un sommet réticulé tel que (v, w) n’est pas une arête dans l’arbre de traversée, il n’y a pas de connaissance préalable de l’état qui sera attribué ultérieurement au sommet réticulé w. Ainsi, s(v, w)(i) ne peut être une borne inférieure des arêtes du réseau situées en dessous du sommet v que si le sommet v est affecté à l’état i. Le raisonnement en est que s(v, w)(i) est le coût de substitution de l’état i au sommet v à un autre état en w le moins coûteux, au lieu du coût de substitution de l’état i en v à l’état en w qui sera affecté ultérieurement. Puisque la définition de S v(i) dépend de la définition de s(v, w)(i), et qu’ils sont définis récursivement, nous observons ce qui suit: S v(i) est une borne inférieure sur la somme des coûts de substitution le long des bords du réseau accessibles à partir du sommet v, à condition que v se voit attribuer l’état i et que tous les sommets de l’arbre descendant se voient attribuer un état unique, et que les sommets réticulés se voient attribuer deux états qui ne sont pas nécessairement les mêmes. Les états assignés du sommet réticulé contribuent à un conflit si les états ne sont pas les mêmes. Supposons que l’état i soit affecté au sommet racine r et que tous les sommets de l’arbre se voient attribuer un état unique, tandis que les sommets réticulés se voient attribuer deux états. Alors le coût S r(i) désigne la somme minimale possible des coûts de substitution le long de toutes les arêtes d’un arbre de traversée avec l’un des états affectés aux sommets réticulés, plus la somme des coûts de substitution le long des arêtes réticulées restantes avec l’état d’affectation alternatif aux sommets réticulés. Puisque nous recherchons une affectation sur les sommets du réseau sans conflits dans les sommets réticulés, S r(i) est une borne inférieure sur le coût d’une telle affectation où le sommet racine est affecté i et tous les sommets sont affectés d’une affectation unique.

Pendant cette phase, on mémorise également les états

pour pouvoir revenir en arrière sur l’état de w qui réalise la quantité s(v, w)(i) pendant la phase de précommande. Voir Algorithme 1.

Pré-commande de la phase de traversée: Nous choisissons d’abord le minimum

où r est le sommet racine et assignons l’état qui atteint le minimum au sommet racine, c’est-à-dire, soit λ^(r) = i r tel que S r(i r) = S. Pour tout autre sommet w qui n’est pas un sommet réticulé, dont le parent v est déjà affecté d’un état i, on attribue l’état t(v, w)(i). Pour un sommet réticulé w dont les sommets parents sont v et v’, supposons que v et v’ se voient attribuer des états i et i’ respectivement lors de la traversée par le pré-ordre. Les états possibles j = t(v, w)(i) et j ‘ = t(v’, w)(i’) de w qui atteignent respectivement s(v, w)(i) et s(v’, w)(i’) ne doivent pas être les mêmes. En d’autres termes, il est possible que j j j ‘. Dans ce cas, on a un conflit sur le sommet réticulé w. Ainsi, la technique de programmation dynamique ne donne pas d’extension pour λ dont le score de parcimonie est S. Dans ce cas, on choisit simplement entre j et j’ pour λ(w) selon lequel des sommets parmi v et v’ est traversé en premier dans le pré-ordre. Ainsi, si le sommet w satisfait la condition de traversée par rapport à v on a λ^(w) =j.

Après avoir terminé la phase de précommande, on peut obtenir le score correspondant à l’extension λ^ en définissant d’abord S’=S et en mettant à jour S’ à chaque sommet réticulé w comme suit: Le score de borne supérieure S’ est mis à jour correspondent à l’affectation j au sommet w en tant que S’- c i ‘j’ + c i’ j. Voir Algorithme 2. La figure 2 montre un exemple de fonctionnement de l’algorithme sur un réseau. Puisque S r(i) est une borne inférieure sur l’affectation optimale où le sommet racine est affecté i et tous les sommets sont affectés d’une affectation unique, et puisque S = min i S r (i), nous concluons que S est une borne inférieure de l’optimum que nous cherchons à trouver. Voir Lemme 1 pour une preuve formelle.

Solution de programmation dynamique. La solution de programmation dynamique appliquée à un réseau phylogénétique. Les états sont 0, 1 et 2. La matrice de coûts utilisée a tous les 1 à l’exception des éléments diagonaux qui sont tous les 0. Les tableaux affichés sur chaque sommet v sont les coûts, S v(i) (deuxième ligne) de chaque état, i (première ligne) qui sont calculés lors de la traversée post-ordre. Les états de l’enfant w, à savoir le t(v, w)(i) (troisième rangée) qui correspondent aux coûts de la deuxième rangée, sont également représentés aux sommets ; lorsqu’il y a deux enfants pour un sommet, les entrées de la troisième rangée sont représentées par une paire d’états de l’enfant gauche et de l’enfant droit respectivement. Chaque arête (v, w) est marquée par s(v, w)(i) pour chaque état i. Lors de la traversée de précommande, les états de chaque sommet sont sélectionnés (indiqués en gras). Le coût de 2 mis en évidence en gras au sommet racine donne une borne inférieure, S. L’état attribué à chaque sommet est mis en évidence en gras. L’algorithme trouve un total de trois substitutions (mises en évidence par des bords en gras). En effet, les états affectés aux sommets parents du sommet réticulé donnent des affectations contradictoires de 1 et 2 respectivement, dont l’état 1 est affecté au sommet réticulé. Ainsi avec un surcoût de 1, on obtient le score de 3 (une borne supérieure du score optimal) comme score de parcimonie correspondant à l’affectation indiquée. Notez que le score de parcimonie optimal sur le réseau est 2 (égal à la borne inférieure), qui peut être trouvé par une recherche exhaustive et peut être réalisé en changeant l’affectation de 1 à 2 pour le parent gauche du sommet réticulé et de 1 à 2 pour le sommet réticulé. Ainsi, la borne inférieure correspond au score optimal, bien que l’affectation correspondant à la borne inférieure ne soit pas sans conflit et ne soit pas la même que l’affectation correspondant à l’optimum.

Lemme 1. La quantité S est une borne inférieure du score de parcimonie optimal sur le réseau N.

Preuve. Par la construction de S, on a

où la deuxième somme est pour le sommet réticulé w avec les parents sont v et v’, tels que v satisfait la condition de traversée w.r.t.w. Ainsi le coût c λ ^(v), λ^(w) est le coût de substitution de l’état attribué λ^(v) à v à l’état λ^(w) à w. D’autre part, le coût c λ^(v’), t(v’, w)(λ^(v’)) est le coût de substitution de l’état attribué λ^(v) à v à l’état t(v’, w)(λ^(v’)) à w. Notez que l’état t(v’, w)(λ^(v’)) n’est pas nécessairement le même que l’état λ^(w), et S est le minimum parmi toutes les affectations pouvant entraîner des conflits aux sommets réticulés.

Supposons que S^ est le score de parcimonie optimal sur N avec la fonction μ: V(N) → {0, 1,…, /Σ/-1 } comme extension de λ on a

où dans la deuxième sommation w est un sommet réticulé avec les parents v et v’. Puisque μ est une affectation sans conflit qui est contenue dans l’ensemble de toutes les affectations dont les coûts S sont le minimum (comparez les équations (3) et (4)), nous avons S≤ S ^. □

Maintenant pour la complexité de l’algorithme. Supposons que le réseau N ait n feuilles et r sommets réticulés. Alors le nombre de sommets dans N est 2 (n + r) -1. A chaque sommet v et pour chaque état i, la quantité S peut être calculée en temps O(k2), où k =|Σ|. L’étape de traversée de pré-commande consiste à trouver S en complexité O(k) et à attribuer les meilleurs états pour chaque sommet. De plus, la fixation d’états de sommets réticulés conflictuels prend du temps O(r). Ainsi la complexité de l’algorithme (présenté ici) pour trouver une borne inférieure et une borne supérieure est O((n+r)k2). Une borne supérieure alternative peut être obtenue en O(nk2) en assignant simplement, pendant la phase de traversée post-ordre, pour chaque sommet réticulé l’état qui se produit le nombre maximal de fois aux feuilles accessibles à partir du sommet réticulé respectif ; et en procédant par la recherche de S v(i) pour les sommets restants. L’optimum exact peut également être obtenu en limitant les états possibles à un seul état pour chaque sommet réticulé, en exécutant l’algorithme de programmation dynamique pour chacune des combinaisons d’états kr pour les sommets réticulés, et en choisissant le minimum parmi tous. La complexité temporelle de ce processus est O (nkr +2).

Algorithme 1 Phase de traversée post-ordre : Calculer le coût de chaque état à chaque sommet

1. 1 :

   Entrée : Réseau N et les états observés à partir de Σ aux feuilles de N, c’est-à-dire une fonction d’affectation d’état λ sur l’alphabet Σ pour N.

2. 2 :

   Pour chaque feuille v, soit S v(i) = 0 si λ(v) = i et ∞ sinon.

3. 3:

   Répéter en post-ordre pour chaque sommet interne (racine, sommet d’arbre interne ou sommet réticulé) v dans N: Pour chaque état i, calculez S v(i) donné en (1) et t(v, w)(i) pour chaque enfant w de v, donné en (2).

4. 4:

   Sortie : {(S v(i),): v ∈ V(N), i ∈ Σ}.

Minimiser le nombre de mutations sur un réseau phylogénétique

L’algorithme Fitch compte le nombre de changements dans un arbre phylogénétique bifurquant pour n’importe quel jeu de caractères, où les états peuvent passer de n’importe quel état à n’importe quel autre état. Ainsi, la matrice de coût est telle que ses éléments diagonaux sont tous des zéros et les éléments hors diagonale sont tous des uns. Dans cette section, nous montrons comment l’algorithme de Fitch s’étend à la recherche de bornes supérieures et inférieures pour le nombre de changements évolutifs dans un réseau phylogénétique donné. Tout d’abord, nous montrons que l’algorithme de Fitch peut être étendu pour donner une borne supérieure pour le score de parcimonie optimal. Comme précédemment, les phases de traversée de post-commande et de pré-commande sont données dans les algorithmes 3 et 4 ci-dessous. Voir la figure 3 pour un exemple d’exécution de l’algorithme.

Phase de traversée de pré-commande de l’algorithme 2: Calculer les bornes inférieure et supérieure de l’optimum et l’affectation correspondante de la borne supérieure

1. 1 :

   Entrée : {(S v(i),): v ∈ V(N), i ∈ Σ}.

2. 2:

   Soit S = min i S r(i), où r est le sommet racine et soit λ^(r) = arg min i S r(i).

3. 3 :

   Soit S ‘ =S

4. 4 :

   Pour chaque sommet w en précommande dont le sommet parent v précède immédiatement w dans le précommande, soit λ^(ω) = t v, w(i), où i = λ^(v).

5. 5:

   Visitez chaque sommet réticulé w avec les parents v et v’ tels que w satisfasse la condition de traversée par rapport à v, avec i = λ ^(v), i ‘ = λ^(v’), j’ = t(v’, w)(i) et mettez à jour S’ comme suit :

   S’ ← S’- c i ‘ j’ + c i’j.
6. 6:

   Sortie: (Borne inférieure, borne supérieure) =(S, S’); extension correspondant au score de borne supérieure S’: λ^.

Algorithme 3 Phase de traversée post-ordre : Calculer l’optimum

1. 1:

   Entrée: Réseau phylogénétique N et une fonction d’affectation d’état λ sur l’alphabet Σ pour N.

2. 2 :

   Pour chaque feuille v de N, on nous donne A(v) ={λ(v)}, un ensemble singleton contenant l’état observé à la feuille.

3. 3:

   Définir UB= 0.

4. 4:

   Récursionner en post-ordre : Pour un sommet v de T avec des enfants w1 et w2, soit et Si le sommet v a un seul enfant w, alors

et

5:({A(v):v ∈ V(N)}, UB)

Puisque la phase de traversée de pré-ordre donne une affectation sans conflit sur les sommets, UB est une borne supérieure. C’est un cas particulier de l’algorithme dynamique présenté pour la matrice de coûts générale. Supposons que nous limitons N à un réseau phylogénétique sans réticulations sœurs, alors toute solution de Fitch sur n’importe quel arbre T dans T(N) forme une borne inférieure pour le score optimal sur les réseaux; et l’ajout du coût sur les bords non en T donne une limite supérieure pour le score optimal. Ainsi, il est possible de calculer notre borne inférieure pour compter le nombre de changements de caractères uniquement pour les réseaux phylogénétiques sans réticulations sœurs, où il est simple de trouver un arbre dans T(N).

Algorithme 4 Phase de traversée de pré-commande : Attribution des états

1. 1 :

   Entrée : Arbre phylogénétique N et ({A(v) : v ∈ V(N)}, UB).

2. 2:

   Pour chaque sommet v de l’arbre qui n’est pas déjà affecté, l’algorithme calcule λ^(v) comme suit: Pour la racine r, λ^(r) = σ, où σ est un élément arbitraire de A(r). Assigner récursivement par précommande : Pour un sommet v dont le parent u est assigné,

   λ^(v) = λ^(u) si λ^(u) ∈ A(v) ; σ ∈ A(v) sinon.

3. 3 :

   Fixation du score : pour chaque sommet réticulé v, si u’ n’est pas le parent en pré-ordre, et si λ^(u’) ∈A(v), mais λ^(u’) ≠ λ^(v), alors incrémentez UB de 1.

4. 4:

   Sortie : UB et fonction d’extension λ^ de λ.