L’hérésie se décline en différents niveaux. Pour l’intellectuel moderne, les niveaux les plus bas d’hérésie pourraient concerner la politique ou l’économie – des domaines de pensée où vous êtes autorisé à avoir des idées peu orthodoxes sans être exclu de la compagnie polie. Des niveaux plus élevés d’hérésie pourraient concerner la religion ou la science – en désaccord avec les hypothèses orthodoxes ici, et vous serez considéré comme tout à fait-peut-être-fou. Le plus haut niveau d’hérésie dans le monde moderne est l’hérésie mathématique. Le désaccord avec l’orthodoxie mathématique est synonyme d ‘ »être une manivelle à part entière. »Vous n’êtes tout simplement pas autorisé à douter de certaines idées en mathématiques sans être condamné comme lépreux intellectuel.
Malheureusement, comme pour tout autre domaine de pensée, il existe une relation inverse entre « acceptabilité du désaccord” et « probabilité d’erreur ». »Plus il est tabou de contester une hypothèse, plus elle risque de s’effondrer sous un examen minutieux. Les théologiens peuvent tolérer un désaccord sur les propriétés de Dieu, mais ils ne peuvent tolérer un désaccord sur l’existence de Dieu. Son existence est trop fondamentale pour être révisée. Si Dieu n’existe pas, toute la structure théorique construite sur cette hypothèse est détruite.
C’est donc avec les mathématiques. Plusieurs hypothèses fondamentales ne peuvent être contestées et se sont donc transformées en dogme, ce qui fait de cet article une hérésie mathématique.
J’ai examiné les fondements de la géométrie standard et j’ai trouvé deux erreurs – l’une logique, l’autre métaphysique. Cet article se concentrera sur la métaphysique. Les objets essentiels décrits par les mathématiciens n’existent pas. Ainsi, toutes les conclusions dérivées sur la base de l’existence de ces objets sont probablement incorrectes.
Dans ce cas, l’affirmation universellement acceptée selon laquelle « Pi est un nombre irrationnel et transcendantal dont la grandeur ne peut pas être exprimée par une expansion décimale finie” est fausse à cause d’une erreur métaphysique.
Pi est un nombre rationnel à expansion décimale finie. Cette idée, qui peut sembler inconcevable au premier abord, se révélera extrêmement raisonnable à la fin de cet article.
(Pour la suite de cet article, je vais abréger « Pi est un nombre rationnel à expansion décimale finie » comme « Pi est un nombre fini » ou plus simplement, « Pi est fini. »)
Sur les formes
Mes revendications sont simples et préservent l’intuition géométrique de base. Par exemple, il s’agit d’un « cercle” :

Ceci est une « ligne”:

Et ce sont des « points”:

Si vous croyez que ces objets sont en effet des cercles, des lignes et des points, alors vous aussi croyez que pi est fini. Vous voyez, les mathématiciens ne croient pas que ces objets soient qualifiés de « lignes” ou de « points ».”Dans leur esprit, les lignes et les points ne peuvent pas être vus, et en fait, ils diraient que les « lignes et points” ci-dessus ne sont que des approximations imparfaites de lignes et de points.
Pour comprendre pourquoi, nous devons poser un ensemble de questions dont les réponses que les gens supposent ont déjà été triées. Ce sont des questions qui sont supposées si évidentes qu’elles ne valent pas la peine d’être posées. Et pourtant, lorsque nous leur demandons des mathématiciens, nous obtenons des réponses douteuses. Des questions comme :
Qu’est-ce qu’une « forme” ?
Qu’est-ce qu’une « ligne » ?
Qu’est-ce qu’un ”point » ?
Qu’est-ce qu’un « cercle” ?
Qu’est-ce que la « distance » ?
Posez ces questions à votre intellectuel moyen, et ils se moqueront probablement de vous, car ils supposent: « Tout le monde sait ce qu’est une ligne! »Ils ont tort. Pour ma part, je ne pense pas que les mathématiciens sachent ce que sont les lignes. Et parce que leurs théories sont construites sur leurs revendications métaphysiques sur les « lignes et les points”, les théories doivent être révisées à partir de zéro.
Sans Longueur, Largeur ou Sens
Comme pi fait l’objet de cet article, exposons la définition que nous avons tous apprise à l’école:
Pi est le rapport de la circonférence d’un cercle à son diamètre.
Nous avons quelques termes clés ici: « le rapport”, »un cercle”, « circonférence” et « diamètre”.
Pour comprendre ce qu’est pi, nous devons comprendre ce que signifient ces autres termes. Surtout celui-ci: « un cercle. »Voici une définition :
Un « cercle” est une forme dont la limite est constituée de points équidistants d’un point fixe.
Cela semble raisonnable. Quelques autres termes clés que nous devons comprendre: « forme”, « limite” et « points.”Si nous voulons comprendre pi, nous devons comprendre ce que sont les cercles, et si nous voulons comprendre ce que sont les cercles, nous devons d’abord comprendre ce que sont les « points”.
C’est ici que je trouve l’erreur fondamentale qui afflige la géométrie orthodoxe : la définition d’un point, à partir duquel tous les autres objets géométriques sont construits. Qu’est-ce qu’un point? Il s’avère qu’il existe de nombreuses définitions différentes. Nous allons commencer par la définition originale d’Euclide, que j’aime bien.
Un « point” est celui qui n’a pas de partie.
Nous reviendrons sur cette définition plus tard. En voici un autre:
Un « point” est un emplacement ou un endroit précis sur un avion.
Pas mal. Ils sont souvent représentés par de petits points :

Cependant, ces définitions intuitives ne sont pas réellement réalisables dans les mathématiques modernes. Les « points », en géométrie orthodoxe, ne sont pas vraiment ”définis » en soi. Ils sont censés être compris en termes de leurs propriétés. Une propriété essentielle est la suivante :
Les points n’ont pas de longueur, d’aire, de volume ou tout autre attribut dimensionnel. Ce sont des objets ”à dimension zéro ».
Ceci est absolument fondamental pour les conceptions modernes de la géométrie. Les points ne peuvent pas avoir de longueur, de largeur ou de profondeur. Et pourtant, toutes les formes sont censées être construites à partir d’elles. Vous pourriez donc vous demander: « Accrochez-vous, comment les formes, qui ont des dimensions, peuvent-elles être composées d’un tas de points qui n’ont pas de dimensions? »
C’est une très bonne question, et si vous insistez pour trouver une réponse logique, vous finirez comme moi: rejeter de très grandes parties des mathématiques orthodoxes.
Chaque « ligne », pour un mathématicien, est en fait composée d’un nombre infini de points – pourtant, chaque point est lui-même sans dimension. Les lignes, qui ont une longueur, sont composées de points, qui n’ont pas de longueur. En quoi cela a-t-il un sens?
Ce n’est pas le cas.
C’est comme demander: « Combien de 0 devez-vous additionner pour obtenir un 1?”La réponse est évidente: vous ne pouvez pas ajouter un tas de 0 ensemble et obtenir un 1 – même pas une quantité infinie de 0. Si un point a des dimensions nulles, peu importe le nombre que vous avez mis ensemble. Vous ne finirez jamais avec un objet dimensionnel. C’est une nécessité logique.
Nous avons donc un très gros problème. La base littérale sur laquelle toute la structure théorique de la géométrie moderne est construite – le « point” – est douteuse. Les erreurs à ce niveau pourraient être catastrophiques.
Formes Sans forme
Si elles sont cohérentes, le mathématicien se force rapidement dans des positions impaires. Par exemple, il doit conclure des choses comme : « Nous ne pouvons pas voir les formes! »Prenons l’exemple de ce que les non-mathématiciens appellent une « ligne”:

Certes, cela ne peut pas être une ligne pour un mathématicien, car les lignes ne sont censées avoir qu’une seule dimension-longueur. Cet objet a à la fois une longueur et une largeur – il est étendu en deux dimensions. Comment pouvons-nous appeler cette forme, alors, sinon une « ligne”? Je ne sais pas – vous devrez demander à un mathématicien.
Qu’en est-il d’un objet bidimensionnel : le cercle ?

Certes, cela ne peut pas être un cercle. Cet objet est composé de pixels, pas de points, et chaque pixel est lui-même étendu en deux dimensions. Par conséquent, l’objet a des bords rugueux et n’est pas parfaitement lisse. Bien que les profanes puissent l’appeler un « cercle », ce n’est qu’une simple approximation du cercle mathématique, parfois appelé le « cercle parfait ».”
La même chose peut être dite pour le mystérieux « point »:

Ces objets ne peuvent pas non plus être qualifiés de « points”, car ils ont des dimensions. Nous pouvons les voir, après tout. Les objets mathématiques ne peuvent pas être vus; ils ne peuvent pas être visualisés; ils ne peuvent avoir aucune forme étendue – ou « réelle” –. Si un objet a réellement une forme, s’il prend de l’espace, il doit être composé d’objets spatialement étendus, semblables à des pixels d’ordinateur, et non à des points mathématiques.
Remarque: Je ne parle pas seulement d' »espace physique » ou de « forme physique ». Je parle de formes de toutes sortes. Ce que je vois dans mon champ visuel – des taches de couleur – ont une forme, mais ce ne sont pas des objets physiques. Ils n’occupent pas eux-mêmes l’espace physique. Ce sont des représentations mentales, et elles sont constituées de points étendus de pixels lumineux sur mon écran mental.
Ainsi, une question naturelle se pose:
Quelqu’un a-t-il déjà vu ou expérimenté ces formes mathématiques de quelque manière que ce soit? Quelqu’un a-t-il rencontré ne serait-ce qu’une seule vraie « ligne” ou « cercle”? La réponse doit être un « Non » catégorique. »Toutes les « lignes » et les « cercles » que nous expérimentons réellement ont des dimensions. Ils sont construits à partir d’un nombre fini de points qui ont eux-mêmes des dimensions. Les objets que nous expérimentons sont composés de pixels.
L’importance de ce point ne peut être surestimée.
Cela signifie que chaque « cercle » que vous avez jamais vu – ou qu’un ingénieur a déjà couché sur papier – a en fait un rapport rationnel de sa circonférence à son diamètre. Chaque « cercle » qui a déjà été rencontré a un ”pi » unique qui peut être exprimé sous forme de rapport de deux entiers.
La « circonférence », pour tout cercle que nous pouvons expérimenter, peut être comprise comme ”la limite la plus extérieure de la forme », elle-même composée d’un nombre fini de pixels. Son « diamètre » est également un simple entier – le nombre de pixels qui le composent. Mettez un entier comme numérateur et un entier comme dénominateur, et vous avez un pi rationnel.
En fait, ces vérités devraient être non controversées, même pour les mathématiciens:
Chaque « cercle » que vous avez jamais rencontré, sans exception, a un pi rationnel et fini.
Aucun « cercle » que vous n’avez jamais rencontré, sans exception, n’a un pi irrationnel.
Donc, cela signifie que mes affirmations sur un « pi rationnel” sont vraies pour au moins 99,9999% de toutes les formes que nous appelons « cercles”. Cela signifie également que pi est unique à un cercle donné. Cela ne devrait pas être une surprise, cependant, lorsque vous pensez à la nature des ratios.
Imaginez que je devais dire: « Quel est le rapport entre la hauteur et la longueur d’une table? »
Vous répondriez naturellement, » Quelle table?”
Il en va de même pour les cercles. Il n’y a pas « un rapport vrai appelé ”pi » » pour la même raison, il n’y a pas « un rapport vrai de la hauteur d’une table à la longueur. »Chaque table, et chaque cercle, est construit par un nombre fini d’unités, disposées de différentes manières, et donc leurs rapports varieront.
Selon la géométrie standard, il n’y a littéralement qu’un seul « cercle” pour lequel mes affirmations ne sont pas vraies: le soi-disant « Cercle parfait” – un objet si mystérieux qu’aucun mortel ne l’a jamais rencontré.
La Forme divine
Ce « cercle parfait » n’a pas de côtés ou de bords mesurables. Sa limite est composée d’un nombre infini de points de dimension zéro. Les points les plus extérieurs occupent exactement zéro espace. Son pi ne peut pas être exprimé par une expansion décimale – et nous ne saurons jamais exactement ce qu’est son pi.
Cet objet ne peut pas être construit, visualisé, ni même exister dans notre monde. Notre monde est trop imparfait pour cela. Au lieu de cela, il vit dans un autre royaume auquel nos esprits peuvent faiblement accéder.
Le Cercle parfait est si grand que tous les autres « cercles” en sont de simples approximations. C’est le seul vrai cercle. Si vous demandez une preuve de son existence, vous n’en trouverez aucune. Pourtant, les mathématiciens ont construit toute leur théorie géométrique basée sur son existence.
J’admets librement mon hérésie : je ne crois pas au « cercle parfait « . »
Par conséquent, je ne crois pas au « pi irrationnel. »Je n’ai pas non plus besoin d’un tel concept. Chaque forme que j’ai jamais rencontrée – ou que je rencontrerai jamais – a des bords qui prennent de la place.
Une géométrie sans cercles parfaits, et sans le pi irrationnel, suffit amplement à expliquer tous les phénomènes que j’expérimente. Par conséquent, je n’ai pas besoin de poser une entité supplémentaire – en particulier une entité avec des propriétés aussi remarquables.
En d’autres termes: Je crois simplement en un cercle de moins que les mathématiciens. C’est tout ce qui est nécessaire pour conclure que pi est un nombre rationnel pour un cercle donné.
Juste une abstraction !
J’ai entendu certains mathématiciens affirmer que les objets géométriques ne sont que des abstractions et sont donc exempts de la critique précédente. Mais entre autres choses, cela fait reculer la métaphysique de l’abstraction. Vous abstraites des bétons. Vous ne concrétisez pas de l’abstrait.
Pensez-y. De quoi s’abstraire pour obtenir le concept de ”cercle parfait »?
Ce ne peut pas être les cercles que nous voyons réellement, car chacun de ces cercles a des bords imparfaits. Toutes les expériences concrètes que nous avons sont des formes aux bords imparfaits, un pi rationnel, et sont composées de points de dimension. Ainsi, à partir de ces expériences, le mathématicien dit: « Eh bien, je pense qu’un cercle vrai est un cercle sans arêtes, avec un pi irrationnel, et est composé de points de dimension zéro!”
C’est un non-sens, et ce n’est pas comme ça que fonctionne l’abstraction.
Imaginez que nous parlons de maisons et de conceptions abstraites des maisons.
Chaque maison que nous avons rencontrée a des murs, un sol et un plafond. Le mathématicien veut dire que sa conception d’une ”maison parfaite » est celle sans murs, sols ou plafond. Et en fait, les vieilles maisons régulières ne sont que des approximations de sa maison parfaite. Évidemment, c’est une erreur.
Nous pouvons avoir une conception abstraite parfaitement valide d’une maison, mais les propriétés de notre « maison abstraite” doivent inclure les propriétés des maisons en béton dont nous faisons abstraction. Notre « maison mentale » doit inclure les catégories conceptuelles de « avoir des murs, des sols et un plafond.” Les dimensions de ces propriétés ne sont pas pertinentes, tant qu’elles existent.
Une conception abstraite d’”une maison sans murs, sols ou plafond » ne peut expliquer aucun phénomène que nous expérimentons, car elle ne décrit rien qui puisse exister. Imaginez que votre ami vous emmène dans un champ vide et vous dise: « Voici ma maison parfaite! Il n’y a pas de murs, de sols ou de plafond! »On pourrait penser qu’il était fou – surtout s’il ajoutait: « Et toutes les autres maisons en sont une simple approximation! »
Pas réel!
L’une des réponses les plus auto-incriminantes des mathématiciens est la suivante: « Mais les objets mathématiques ne sont pas réels! Ils n’existent pas du tout !”Dans toutes mes recherches, je peux affirmer avec confiance que les mathématiques sont le seul domaine de pensée où admettre que « les objets dont je parle ne sont pas réels et n’existent pas” est destiné à défendre une théorie particulière.
Cette erreur est une confusion d’objets et de leurs référents. Par exemple, le concept de « ma maison » est censé faire référence à « ma maison dans le monde. »Ce serait idiot de dire « Ma maison ne prend pas de place, parce que mon idée de ma maison ne prend pas de place. »
De même, la conception d’un ”point » est censée faire référence à » un emplacement précis dans l’espace géométrique.”Ce serait tout aussi idiot de dire « les points ne prennent pas d’espace géométrique, parce que mon idée d’un point n’occupe pas d’espace géométrique. »
L’essence fondamentale de la géométrie concerne l’espace – qu’il s’agisse d’espace physique, d’espace mental, d’espace conceptuel ou de tout autre type d’espace. Par conséquent, les objets de la géométrie doivent eux-mêmes prendre de la place. Il n’existe pas de » localisation précise dans l’espace qui ne soit pas une localisation précise dans l’espace. »
Une théorie alternative
Alors, permettez-moi de présenter un cadre géométrique alternatif. Ce n’est que le début d’une toute nouvelle théorie des mathématiques que j’appelle « mathématiques des unités de base. »Ce sont les principes fondamentaux de la géométrie des unités de base:
1)Toutes les structures géométriques sont composées d’unités de base. Ces unités sont appelées « points. »
2) Chaque point est étendu spatialement.
3) Dans tout cadre conceptuel, l’extension de l’unité de base est exactement 1. Dans ce cadre, il n’y a pas de plus petite unité de distance, par définition.
4) Toutes les distances et formes peuvent être libellées en termes d’unité de base.
Ces fondations forment une base logiquement solide sur laquelle construire la géométrie.
Assemblez des points et vous pouvez composer n’importe quelle forme de votre choix, sans aucun nombre irrationnel. Chaque objet à l’exception de l’unité de base est un objet composite, composé de points discrets. C’est pourquoi j’ai dit plus tôt que j’aime la définition originale d’Euclide d’un « point” comme « ce qui n’a pas de partie. »Les unités de base n’ont pas de parties; ce sont les parties qui forment un tout sur deux.
Je reconnais qu’il y aura beaucoup d’objections à cette façon de penser la géométrie. Ces objections seront traitées en détail dans les prochains articles.
Pour avoir une intuition sur ce cadre, vous pouvez considérer les « points » comme des « pixels”, dont nous avons tous l’expérience. Toutes les formes et objets que vous pourriez rencontrer dans une simulation VR haute résolution sont en fait des amas de pixels, bien qu’ils puissent sembler « parfaitement lisses” de notre perspective macroscopique.
Quelques-unes des implications intéressantes de cette théorie:
Ceci est une ligne:

Ceci est un cercle:

Et il a un pi manifestement rationnel:
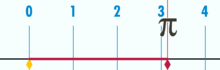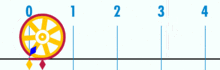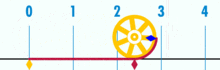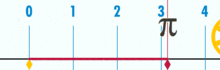
(Remarque: ce GIF a été tiré de Wikipedia pour montrer l’irrationalité supposée de pi. Pourtant, si vous êtes conscient de ce que vous regardez, c’est en fait une démonstration de la rationalité de pi. Vous regardez un GIF de la perfection logique et de la précision de la géométrie de l’unité de base!)
Quel est le rapport de la circonférence de ce cercle au diamètre? Simple: c’est un entier sur un autre – quelle que soit la quantité d’unités de base qui composent la circonférence, divisée par la quantité d’unités qui composent le diamètre. Et, comme il se trouve, tant que le cercle n’est pas construit à partir d’une infime quantité d’unités de base, les rapports pi fonctionneront à environ 3.14159 (Cependant, si nous sommes parfaitement précis, nous devons nommer en termes de fractions, car l’expansion décimale peut être douteuse dans un cadre d’unités de base. Mais c’est un futur article.). Il n’y a pas de cercle « générique” ou « idéal”. Il existe des cercles concrets, réels, dont chacun est un objet composite construit par un nombre fini de points.
Entre autres choses, cela signifie également qu’il n’existe pas de « cercle unitaire” – un cercle supposé de rayon 1. Il n’y a pas de diamètres qui ont une distance de 1. Vous ne pouvez pas créer un cercle en utilisant un seul pixel.
Dans cette théorie, les « cercles » sont exactement ce que vous avez rencontré. Les ”points » sont des emplacements dans l’espace qui sont des emplacements réels dans l’espace, et les ”lignes » sont ce que tout le monde sait qu’elles sont.
Intuition des unités de base
De toute évidence, ce sujet nécessite beaucoup plus d’explications et de travail, pas seulement en géométrie, mais partout où la métaphysique des mathématiques se trompe. Je ne peux pas couvrir toutes les objections à la géométrie des unités de base dans cet article, mais je vais expliquer quelques autres façons de penser à ce sujet et pourquoi elle est supérieure à l’orthodoxie standard.
Tout d’abord, ce cadre explique pleinement tous les phénomènes que nous expérimentons, et il perd exactement zéro pouvoir explicatif par rapport à la géométrie standard. Chaque forme, chaque cercle, chaque ligne, chaque point, chaque expérience spatiale que nous aurons peut être expliquée, sans poser l’existence d’entités supplémentaires. Nous ne faisons pas l’expérience de cercles parfaits; nous n’avons donc aucune raison de théoriser à leur sujet.
De plus, les mathématiques des unités de base sont plus logiquement précises que l’orthodoxie. Quiconque a travaillé avec des « pi irrationnels » doit utiliser des approximations. Ils ne peuvent pas utiliser une expansion décimale infinie réelle. Ils sont obligés de couper arbitrairement la magnitude pour pi afin de l’utiliser. Ce n’est pas le cas avec la géométrie de l’unité de base. Une précision parfaite est en fait possible, car il n’y a pas d’approximations ou d’expansions décimales infinies à traiter. Ce n’est peut-être pas un gros problème en ce moment, mais à mesure que la technologie se rapproche des dimensions de l’unité de base de l’espace physique, cela pourrait faire une grande différence.
Voici un petit aparté intéressant sur l’expansion décimale infinie de pi:
Que se passe-t-il lorsque les mathématiciens orthodoxes calculent de plus en plus de décimales de pi? Saisissent-ils « les vrais ratios du Cercle parfait”? Aucun. Ce qu’ils font, c’est calculer les ratios de pi pour les cercles avec des unités de base de plus en plus petites. Au fur et à mesure que l’unité de base se rétrécit – ou que le cercle grossit de diamètre – le rapport de sa circonférence au diamètre change toujours aussi légèrement. Ces calculs sont immédiatement pratiques, de la même manière que les tables trigonométriques sont pratiques. Ce sont des valeurs pré-calculées qui sont applicables et précises pour un cercle donné d’une taille donnée.
(Si vous voulez comprendre pourquoi pi change légèrement, pensez-y de cette façon: à mesure que la taille de l’unité de base augmente, la surface fermée par la circonférence diminue; à mesure que la taille de l’unité de base diminue, la surface fermée par la circonférence augmente, mais à un rythme décroissant. Plus le bord du cercle est lisse, plus la surface du cercle est grande.)
Sur cette note: la géométrie de l’unité de base ne nécessite pas d' »unité de base ultime.”En d’autres termes, chaque schéma conceptuel aura une unité de base par nécessité logique, mais cela ne signifie pas que vous êtes empêché de proposer un schéma conceptuel différent qui a une unité de base plus petite.
Pensez-y de cette façon: toute photographie donnée contiendra un nombre fini de pixels. Il aura une résolution d’unité de base. Cependant, cela ne signifie pas qu’il est impossible de prendre une photo avec une résolution plus élevée. De même, un cercle donné aura une résolution d’unité de base, mais cela ne signifie pas qu’il est impossible d’en concevoir une avec une résolution plus élevée (unités de base plus petites).
Nous pourrions même rencontrer les limites du monde physique. L’espace physique doit avoir une unité de base, ce qui signifie que dans notre système physique, il n’y a pas d’unité plus petite. Cependant, cela ne signifie pas que nous sommes empêchés de parler d’unités de base de plus petites dimensions. Ces objets ne seront tout simplement pas en corrélation avec notre univers. Qui sait – peut-être pourrions-nous dire des choses vraies sur un univers physique différent qui a des unités de base plus petites.
Remarque: cela correspond également parfaitement à ma résolution des paradoxes de Zénon. L’espace doit avoir une unité de base, si le mouvement est possible.
Un excellent exemple de phénomènes d’unités de base est la fractale. Soi-disant, les fractales n’ont de sens que dans le cadre conceptuel de la « divisibilité infinie. »Ce n’est pas correct. Les fractales ont beaucoup plus de sens dans un contexte d’unité de base. Considérez cette image:

Cela ressemble à un candidat principal pour « divisibilité infinie. »Cependant, c’est une illusion. À tout moment, il existe une résolution d’unité de base pour cette image. Lorsque l’image « zoome », de nouvelles unités sont créées, toutes libellées en pixels. À aucun moment vous ne regardez dans l’infini; vous regardez toujours un nombre fini de pixels. Si vous en doutez, vous pouvez compter les pixels. L’objet est construit pendant que vous le regardez. La même chose se produit en mathématiques; les objets sont construits comme vous les concevez. On en dira beaucoup plus à ce sujet dans de futurs articles.
Polygones et Grecs
Je veux répondre rapidement à une objection qui se posera inévitablement – ceux qui prétendent que les images de cercles dans cet article ne sont pas en fait des cercles; ce sont des polygones. Les bords sont un tas de petites lignes droites; ils ne sont pas parfaitement lisses. Si cela est vrai, ce n’est pas une critique de la géométrie des unités de base, car tous les objets ronds que nous rencontrons seraient des polygones. Par conséquent, nos théories mathématiques devraient porter sur les polygones; nous n’expérimentons rien d’autre. Je veux connaître les propriétés de cette forme:

Je me fiche de ce que vous appelez ça. La géométrie de l’unité de base peut vous renseigner sur les propriétés de cette forme.
Les Grecs ont également commis cette erreur en parlant de cercles – comme s’ils étaient construits à partir d’un « nombre infini de lignes. »C’est incorrect. Les cercles et les polygones sont composés d’un nombre fini de points, pas de lignes. Les lignes ne composent rien ; elles sont elles-mêmes des objets composites.
Imaginez construire un cercle dans le sable.

Quelle est l’aire de ce cercle? Je vous garantis que c’est un nombre fini et rationnel. Vous pouvez littéralement compter les grains de sable qui le composent. La circonférence est composée de grains de sable, tout comme le diamètre, tout comme la zone. Ce sont tous des entiers.
Le dernier argument que j’aborderai dans l’article viendra de ceux qui pensent qu’un ”cercle » n’est pas une forme; c’est une expression mathématique. Quelque chose comme (x2 + y2 = r2).
C’est juste une autre confusion métaphysique qui confond les symboles avec l’objet que les symboles sont censés décrire. C’est comme dire : » Les pommes sont synonymes des mots » un fruit rouge. » C’est confus. Les mots « un fruit rouge » sont une description de l’objet, pas de l’objet lui-même. La formule comme (x2 + y2 = r2) décrira la forme d’un cercle – ou, si vous préférez y penser de cette façon – c’est une règle pour construire un cercle. Ce n’est pas en soi un cercle.
C’est là que je terminerai cet article. Il y a beaucoup plus à dire à l’avenir. Les mathématiques ne sont pas exemptes de critiques ou d’enquêtes sceptiques. Elle n’est pas non plus exempte de la nécessité d’une métaphysique précise. Pour toutes les raisons que j’ai décrites dans cet article, il y a beaucoup de place pour des conceptions alternatives – et supérieures – de la géométrie. La géométrie des unités de base ne perd aucun pouvoir explicatif, élimine un nombre infini d’objets inutiles et donne une base logique sur laquelle construire une théorie plus solide.
Si vous ne croyez pas à l’existence de « cercles parfaits” – composés d’un nombre infini de points de dimension zéro – alors vous ne croyez pas que pi est irrationnel, et vous avez rejoint un groupe extrêmement restreint de lépreux intellectuels. Vous pouvez maintenant vous attendre à des moqueries et à une condamnation pour votre hérésie.
Si vous avez apprécié cet article et que vous souhaitez soutenir la création de plus d’hérésie, visitez patreon.com/stevepatterson .